Тетрадекагон - Tetradecagon

Правильный тетрадекагон
Правильный четырехугольник
Тип	Правильный многоугольник
Края и вершины	14
Символ Шлефли	{14}, т {7}
Диаграмма Кокстера
Группа симметрии	Двугранный (D14), порядок 2 × 14
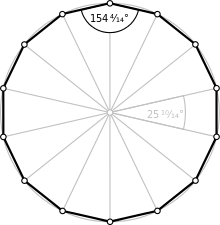
Внутренний угол (градусы )	154+2/7°
Двойной многоугольник	Себя
Характеристики	Выпуклый, циклический, равносторонний, изогональный, изотоксальный

В геометрия, а четырехугольник или четырехугольник или 14-угольник - четырнадцатигранный многоугольник.

Правильный тетрадекагон

А обычный четырехугольник имеет Символ Шлефли {14} и может быть построен как квазирегулярный усеченный семиугольник, t {7}, который чередует два типа ребер.

В площадь из обычный четырехугольник длины стороны а дан кем-то

${displaystyle {egin {align} A & = {frac {14} {4}} a ^ {2} cot {frac {pi} {14}} = {frac {14} {4}} a ^ {2} left ( {frac {{sqrt {7}} + 4 {sqrt {7}} cos left ({{frac {2} {3}} arctan {frac {sqrt {3}} {9}}} ight)} {3} } ight) & simeq 15.3345a ^ {2} конец {выровнено}}}$

строительство

Поскольку 14 = 2 × 7, правильный четырехугольник не может быть построен используя компас и линейка.^[1] Однако его можно построить, используя Neusis с использованием тройной угол,^[2] или с отмеченной линейкой,^[3] как показано в следующих двух примерах.

Тетрадекагон с учитывая описанный круг:
Анимация (1 мин 47 с) из конструкции neusis с радиусом описанной окружности ${displaystyle {overline {OA}} = 6}$,
в соответствии с Эндрю М. Глисон,^[2] на основе трисекция угла с помощью Томагавк., пауза в конце 25 с

Тетрадекагон с заданная длина стороны:
Анимация (1 мин 20 сек) из конструкции neusis с отмеченной линейкой, согласно Дэвиду Джонсону Лейску (Крокетт Джонсон )^[3] для семиугольника пауза в конце 30 с.

На приведенной ниже анимации центральный угол приблизительно равен 0,05 °:

Построение приближенного правильного четырехугольника

Еще одна возможная анимация примерного построения, также возможная с использованием линейки и циркуля.

Обычный четырехугольник, построение аппроксимации в виде анимации (3 мин 16 с), пауза в конце 25 с

На основе единичной окружности r = 1 [единица длины]

• Построенная длина стороны тетрадекагона в GeoGebra (отображение максимум 15 знаков после запятой) ${displaystyle a = 0,445041867912629; [единица; из; длины]}$
• Длина стороны четырехугольника ${displaystyle a_ {target} = 2cdot sin left ({frac {180 ^ {circ}} {14}} ight) = 0,445041867912629ldots; [unit; of; length]}$
• Абсолютная погрешность построенной длины стороны

До макс. отображается 15 знаков после запятой - абсолютная ошибка ${displaystyle F_ {a} = a-a_ {target} = 0,0; [единица; длины]}$

• Построенный центральный угол четырехдесятиугольника в GeoGebra (отображение значащих 13 знаков после запятой) ${displaystyle mu = 25.7142857142857 ^ {circ}}$
• Центральный угол четырехугольника ${displaystyle mu _ {target} = {frac {360 ^ {circ}} {14}} = 25.7142857142857ldots ^ {circ}}$
• Абсолютная погрешность построенного центрального угла

До указанных 13 значащих десятичных знаков - абсолютная погрешность. ${displaystyle F_ {mu} = mu -mu _ {target} = 0 ^ {circ}}$

Пример для иллюстрации ошибки

• По радиусу описанной окружности r = 1 млрд км (свет, необходимый для этого расстояния около 55 минут), абсолютная погрешность 1-й стороны будет <1 мм.

Подробнее см .: Викиучебники: Тетрадекагон, описание конструкции (немецкий)

Симметрия

Симметрии правильного четырехугольника. Вершины окрашены в соответствии с их положением симметрии. Синие зеркала прорисовываются через вершины, а фиолетовые зеркала - через края. В центре даны приказы гирации.

В правильный четырехугольник имеет Dih₁₄ симметрия, порядок 28. Существует 3 диэдральных симметрии подгруппы: Dih₇, Ди₂, и Dih₁, и 4 циклическая группа симметрии: Z₁₄, Z₇, Z₂, а Z₁.

Эти 8 симметрий можно увидеть в 10 различных симметриях на тетрадекагоне, большее число, потому что линии отражения могут проходить через вершины или ребра. Джон Конвей помечает их буквой и групповым порядком.^[4] Полная симметрия правильной формы r28 и симметрия не помечена а1. Диэдральные симметрии разделяются в зависимости от того, проходят ли они через вершины (d для диагонали) или краев (п для перпендикуляров), и я когда линии отражения проходят через ребра и вершины. Циклические симметрии в среднем столбце помечены как грамм для их приказов центрального вращения.

Симметрия каждой подгруппы допускает одну или несколько степеней свободы для неправильных форм. Только g14 подгруппа не имеет степеней свободы, но может рассматриваться как направленные края.

Неправильные тетрадекагоны высшей симметрии - это d14, изогональный тетрадекагон, состоящий из семи зеркал, у которых могут чередоваться длинные и короткие края, и стр. 14, изотоксальный тетрадекагон, состоящий из ребер равной длины, но чередующиеся вершинами под двумя разными внутренними углами. Эти две формы двойники друг друга и имеют половину порядка симметрии правильного тетрадекагона.

Рассечение

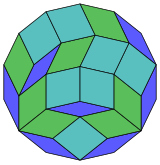
14-куб проекция

84 рассечение ромба

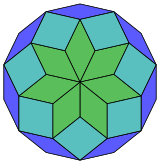
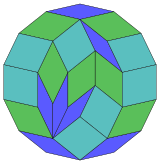
Coxeter заявляет, что каждый зоногон (а 2м-угольник, противоположные стороны которого параллельны и равной длины) можно разрезать на м(м-1) / 2 параллелограмма.^[5]В частности, это верно для правильные многоугольники с равным числом сторон, в этом случае все параллелограммы ромбовидны. Для правильный четырехугольник, м= 7, и его можно разделить на 21: 3 набора по 7 ромбов. Это разложение основано на Многоугольник Петри проекция 7-куб, с 21 из 672 лиц. Список OEIS: A006245 определяет количество решений как 24698, включая до 14-кратных поворотов и хиральных форм в отражении.

Разрез на 21 ромб

Нумизматическое использование

Правильный четырехугольник используется как форма памятного золота и серебра. Малазийский монеты, количество сторон которых представляет 14 штатов Малайзийской Федерации.^[6]

Связанные цифры

Флаг Малайзии с четырнадцатиконечной звездой

А тетрадекаграмма представляет собой 14-сторонний звездообразный многоугольник, представленный символом {14 / n}. Есть два обычных звездные многоугольники: {14/3} и {14/5}, использующие те же вершины, но соединяющие каждую третью или пятую точки. Также есть три соединения: {14/2} сокращается до 2 {7} как два семиугольники, а {14/4} и {14/6} уменьшаются до 2 {7/2} и 2 {7/3} как двух разных гептаграммы, и, наконец, {14/7} сокращается до семи дигоны.

Заметное применение четырнадцатиконечной звезды находится в флаг Малайзии, который включает в себя желтую тетрадекаграмму {14/6} в правом верхнем углу, представляющую единство тринадцати состояния с Федеральное правительство.

Соединения и звездообразные многоугольники
п	1	2	3	4	5	6	7
Форма	Обычный	Сложный	Звездный многоугольник	Сложный	Звездный многоугольник	Сложный
Изображение	{14/1} = {14}	{14/2} = 2{7}	{14/3}	{14/4} = 2{7/2}	{14/5}	{14/6} = 2{7/3}	{14/7} или 7 {2}
Внутренний угол	≈154.286°	≈128.571°	≈102.857°	≈77.1429°	≈51.4286°	≈25.7143°	0°

Более глубокие усечения правильного семиугольника и гептаграммы может образовывать изогональные (вершинно-транзитивный ) промежуточные формы тетрадекаграммы с одинаковыми вершинами и двумя длинами ребер. Другие усечения могут образовывать многоугольники 2 {p / q} с двойным покрытием, а именно: t {7/6} = {14/6} = 2 {7/3}, t {7/4} = {14/4} = 2 {7/2}, а t {7/2} = {14/2} = 2 {7}.^[7]

Изогональные усечения семиугольника и гептаграммы
Квазирегулярный	Изогональный			Квазирегулярный Двойное покрытие
t {7} = {14}				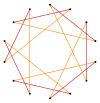{7/6}={14/6} =2{7/3}
т {7/3} = {14/3}				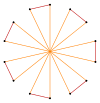т {7/4} = {14/4} =2{7/2}
т {7/5} = {14/5}				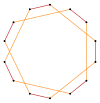т {7/2} = {14/2} =2{7}

Полигоны Петри

Регулярный перекос тетрадекагоны существуют как Многоугольник Петри для многих многомерных многогранников, показанных на этих наклонных ортогональные проекции, включая:

Полигоны Петри
B7		2I2(7) (4D)
7-ортоплекс	7-куб	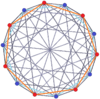7-7 дуопирамида	7-7 дуопризма
А13	D8		E8
13-симплекс	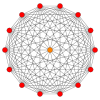511	151	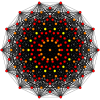421	241

Рекомендации

внешняя ссылка

• Вайсштейн, Эрик В. «Тетрадекагон». MathWorld.