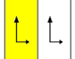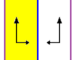Список плоских групп симметрии - Википедия - List of planar symmetry groups

В этой статье обобщены классы дискретный группы симметрии из Евклидова плоскость. Группы симметрии названы здесь тремя схемами именования: Международная нотация, орбифолдная запись, и Обозначение Кокстера.Существуют три вида групп симметрии плоскости:

2 семьи розетки группы - 2D точечные группы
7 фризовые группы - 2D группы линий
17 группы обоев - 2D космические группы.

Розетки группы

Есть два семейства дискретных двумерных точечных групп, и они задаются параметром п, который является порядком группы вращений в группе.

Семья	Intl (орбифолд )	Schön.	Гео ^[1] Coxeter	Заказ	Примеры
Циклическая симметрия	п (п •)	C_п	п [n]⁺	п	C₁, [ ]⁺ (•)	C₂, [2]⁺ (2•)	C₃, [3]⁺ (3•)	C₄, [4]⁺ (4•)	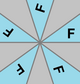C₅, [5]⁺ (5•)	C₆, [6]⁺ (6•)
Двугранная симметрия	пм (* п •)	D_п	п [n]	2п	D₁, [ ] (*•)	D₂, [2] (*2•)	D₃, [3] (*3•)	D₄, [4] (*4•)	D₅, [5] (*5•)	D₆, [6] (*6•)

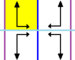
Фриз-группы

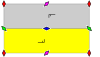
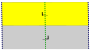
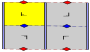
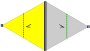
7 фризовые группы, двумерный группы линий, с направлением периодичности даны с пятью условными обозначениями. В Обозначение Шенфлиса задается как бесконечные пределы 7 диэдральных групп. Желтые области представляют собой бесконечную фундаментальную область в каждой.

[1,∞],
IUC (орбифолд )	Гео	Schönflies	Coxeter	Фундаментальный домен	Пример
p1 (∞•)	п1	C_∞	[1,∞]⁺		прыгать
p1m1 (*∞•)	p1	C_∞v	[1,∞]		сбоку

[2,∞⁺],
IUC (орбифолд)	Гео	Schönflies	Coxeter	Фундаментальный домен	Пример
p11g (∞×)	п._грамм1	S_2∞	[2⁺,∞⁺]		шаг
p11m (∞*)	п. 1	C_∞h	[2,∞⁺]		Прыгать

[2,∞],
IUC (орбифолд)	Гео	Schönflies	Coxeter	Пример
p2 (22∞)	п2	D_∞	[2,∞]⁺	прядильный хмель
p2mg (2*∞)	p2_грамм	D_∞d	[2⁺,∞]	вращающийся бочонок
p2мм (*22∞)	p2	D_∞h	[2,∞]	вращающийся прыжок

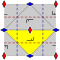
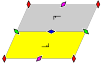
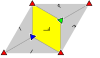
Группы обоев

17 группы обоев, с конечными фундаментальными областями, задаются формулами Международная нотация, орбифолдная запись, и Обозначение Кокстера, классифицируется на 5 Решетки Браве в плоскости: квадрат, наклонный (параллелограмматический), шестиугольный (равносторонний треугольник), прямоугольный (центрированный ромбический) и ромбический (центрированный прямоугольный).

В p1 и p2 группы без отражательной симметрии повторяются во всех классах. Связанное с этим чисто отражающее Группа Кокстера даны со всеми классами, кроме косого.

Квадрат
[4,4],
IUC (Сфера. ) Гео	Coxeter	Фундаментальный домен
p1 (°) п1
p2 (2222) п2	[4,1⁺,4]⁺ [1⁺,4,4,1⁺]⁺
pgg (22×) п_грамм2_грамм	[4⁺,4⁺]
пмм (*2222) p2	[4,1⁺,4] [1⁺,4,4,1⁺]
см (2*22) c2	[(4,4,2⁺)]
p4 (442) п4	[4,4]⁺
p4g (4*2) п_грамм4	[4⁺,4]
p4m (*442) p4	[4,4]

Прямоугольный
[∞_час,2,∞_v],
IUC (Сфера.) Гео	Coxeter	Фундаментальный домен
p1 (°) п1	[∞⁺,2,∞⁺]
p2 (2222) п2	[∞,2,∞]⁺
пг (ч) (××) п_грамм1	ч: [∞⁺,(2,∞)⁺]
пг (v) (××) п_грамм1	v: [(∞, 2)⁺,∞⁺]
pgm (22*) п_грамм2	ч: [(∞, 2)⁺,∞]
pmg (22*) п_грамм2	v: [∞, (2, ∞)⁺]
pm (ч) (**) p1	ч: [∞⁺,2,∞]
pm (v) (**) p1	v: [∞, 2, ∞⁺]
пмм (*2222) p2	[∞,2,∞]

Ромбический
[∞_час,2⁺,∞_v],
IUC (Сфера.) Гео	Coxeter	Фундаментальный домен
p1 (°) п1	[∞⁺,2⁺,∞⁺]
p2 (2222) п2	[∞,2⁺,∞]⁺
см (ч) (*×) c1	ч: [∞⁺,2⁺,∞]
см (v) (*×) c1	v: [∞, 2⁺,∞⁺]
pgg (22×) п_грамм2_грамм	[((∞,2)⁺)^[2]]
см (2*22) c2	[∞,2⁺,∞]

Параллелограмматический (косой )
p1 (°) п1
p2 (2222) п2

Шестиугольный / Треугольный
[6,3], / [3^[3]],
p1 (°) п1
p2 (2222) п2	[6,3]^Δ
см (2*22) c2	[6,3]^⅄
p3 (333) п3	[1⁺,6,3⁺] [3^[3]]⁺
p3m1 (*333) p3	[1⁺,6,3] [3^[3]]
p31m (3*3) h3	[6,3⁺]
p6 (632) п6	[6,3]⁺
p6m (*632) p6	[6,3]

Обои отношения подгруппы

Отношения между подгруппами в группе из 17 обоев^[2]
		о	2222	××	**	*×	22×	22*	*2222	2*22	442	4*2	*442	333	*333	3*3	632	*632
		p1	p2	pg	вечера	см	pgg	pmg	пмм	см	p4	p4g	p4m	p3	p3m1	p31m	p6	p6m
о	p1	2
2222	p2	2	2	2
××	pg	2		2
**	вечера	2		2	2	2
*×	см	2		2	2	3
22×	pgg	4	2	2			3
22*	pmg	4	2	2	2	4	2	3
*2222	пмм	4	2	4	2	4	4	2	2	2
2*22	см	4	2	4	4	2	2	2	2	4
442	p4	4	2								2
4*2	p4g	8	4	4	8	4	2	4	4	2	2	9
*442	p4m	8	4	8	4	4	4	4	2	2	2	2	2
333	p3	3												3
*333	p3m1	6		6	6	3								2	4	3
3*3	p31m	6		6	6	3								2	3	4
632	p6	6	3											2			4
*632	p6m	12	6	12	12	6	6	6	6	3				4	2	2	2	3

Смотрите также

Список групп сферической симметрии
Обозначение орбифолда # Гиперболическая плоскость - группы гиперболической симметрии

Примечания

^ Кристаллографические пространственные группы в геометрической алгебре, Д. Хестенес и Дж. Холт, Журнал математической физики. 48, 023514 (2007) (22 стр.) PDF [1]
^ Кокстер, (1980), 17 групп плоскостей, таблица 4

внешняя ссылка

«Рукопись Конвея» на нотации Орбифолда (Обозначение изменено с этого оригинала, Икс теперь используется вместо открытой точки, а o используется вместо закрытой точки)
17 групп обоев

[1] Кристаллографические пространственные группы в геометрической алгебре, Д. Хестенес и Дж. Холт, Журнал математической физики. 48, 023514 (2007) (22 стр.) PDF [1]

[2] Кокстер, (1980), 17 групп плоскостей, таблица 4

[1]

[2]