Шестиугольник - Hexagon
| Правильный шестиугольник | |
|---|---|
 Правильный шестиугольник | |
| Тип | Правильный многоугольник |
| Края и вершины | 6 |
| Символ Шлефли | {6}, т {3} |
| Диаграмма Кокстера | |
| Группа симметрии | Двугранный (D6), порядок 2 × 6 |
| Внутренний угол (градусы ) | 120° |
| Двойной многоугольник | Я |
| Свойства | Выпуклый, циклический, равносторонний, изогональный, изотоксальный |
В геометрия, а шестиугольник (от Греческий ἕξ шестнадцатеричный, «шестерка» и γωνία, гония, «уголок, угол») - шестигранный многоугольник или 6-угольник. Сумма внутренних углов любого просто (несамопересекающийся) шестиугольник равен 720 °.
Правильный шестиугольник
А регулярный шестиугольник имеет Символ Шлефли {6}[1] а также может быть построен как усеченный равносторонний треугольник, t {3}, который чередует два типа ребер.


Правильный шестиугольник определяется как шестиугольник, который одновременно равносторонний и равносторонний. это бицентрический, что означает, что это оба циклический (имеет описанный круг) и касательный (имеет начертанный кружок).
Общая длина сторон равна радиусу описанный круг или описанный круг, что равно раз апофема (радиус вписанный круг ). Все внутренние углы 120 лет градусы. В правильном шестиугольнике шесть вращательная симметрия (вращательная симметрия шестого порядка) и шесть симметрии отражения (шесть линий симметрии), составляя группа диэдра D6. Самые длинные диагонали правильного шестиугольника, соединяющие диаметрально противоположные вершины, вдвое превышают длину одной стороны. Из этого видно, что треугольник с вершиной в центре правильного шестиугольника и общей с шестиугольником одной стороной равносторонний, и что правильный шестиугольник можно разбить на шесть равносторонних треугольников.
подобно квадраты и равносторонний треугольники, правильные шестиугольники подходят друг к другу без зазоров, чтобы выложить плиткой самолет (три шестиугольника, пересекающиеся в каждой вершине), и поэтому полезны для построения мозаика. Ячейки улей соты имеют шестиугольную форму по этой причине, а также потому, что форма позволяет эффективно использовать пространство и строительные материалы. В Диаграмма Вороного правильной треугольной решетки - это сотовая мозаика из шестиугольников. Обычно это не считается триамбус, хотя и равносторонний.
Параметры

Максимальный диаметр (что соответствует длинному диагональ шестиугольника), D, в два раза больше максимального радиуса или по окружности, р, что равняется длине стороны, т. Минимальный диаметр или диаметр вписанный круг (разделение параллельных сторон, расстояние между плоскостями, короткая диагональ или высота при опоре на плоское основание), d, вдвое меньше минимального радиуса или inradius, р. Максимумы и минимумы связаны одним и тем же фактором:
- и аналогично
Площадь правильного шестиугольника
Для любого обычного многоугольник, площадь также можно выразить через апофема а и периметр п. Для правильного шестиугольника они даются как а = р, и п, так
Правильный шестиугольник заполняет дробь своего описанный круг.
Если правильный шестиугольник имеет последовательные вершины A, B, C, D, E, F и если P - любая точка на описанной окружности между B и C, то ПЭ + ПФ = ПА + ПБ + ПК + ПД.
Из соотношения по окружности к inradius что отношение высоты к ширине правильного шестиугольника составляет 1: 1,1547005; то есть шестиугольник с длинным диагональ 1.0000000 будет иметь расстояние 0,8660254 между параллельными сторонами.
Точка в плоскости
Для произвольной точки плоскости правильного шестиугольника с описанным радиусом , расстояние до центра тяжести правильного шестиугольника и его шести вершин равно и соответственно имеем [2]
Если - расстояния от вершин правильного шестиугольника до любой точки на его описанной окружности, то [2]
Симметрия


В правильный шестиугольник есть Dih6 симметрия, порядок 12. Есть три диэдральные подгруппы: Dih3, Ди2, и Dih1и четыре циклический подгруппы: Z6, Z3, Z2, а Z1.
Эти симметрии выражают девять различных симметрий правильного шестиугольника. Джон Конвей маркирует их буквой и групповым порядком.[3] r12 полная симметрия, и а1 нет симметрии. p6, изогональный шестиугольник, состоящий из трех зеркал, может чередовать длинные и короткие края, и d6, изотоксальный шестиугольник, состоящий из ребер равной длины, но чередующиеся вершинами под двумя разными внутренними углами. Эти две формы двойники друг друга и имеют половину порядка симметрии правильного шестиугольника. В i4 формы - правильные шестиугольники, сплющенные или вытянутые вдоль одного направления симметрии. Это можно рассматривать как удлиненный ромб, в то время как d2 и p2 можно рассматривать как вытянутые по горизонтали и вертикали воздушные змеи. g2 шестиугольники, противоположные стороны которых параллельны, также называются шестиугольниками. параллелогоны.
Симметрия каждой подгруппы допускает одну или несколько степеней свободы для неправильных форм. Только g6 подгруппа не имеет степеней свободы, но может рассматриваться как направленные края.
| Пример шестиугольников по симметрии | |||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
Шестиугольники симметрии g2, i4, и r12, так как параллелогоны может мозаику евклидовой плоскости переводом. Другой формы шестиугольника могут выложить плоскость с разной ориентацией.
| p6m (* 632) | см (2 * 22) | p2 (2222) | p31m (3 * 3) | pmg (22 *) | пг (× ×) | |
|---|---|---|---|---|---|---|
 r12 |  i4 |  g2 |  d2 |  d2 |  p2 |  а1 |
Группы A2 и G2
 Корни группы A2 |  Корни группы G2 |
6 корней простая группа Ли A2, представленный Диаграмма Дынкина ![]()
![]()
![]() , имеют правильный шестиугольный узор. Угол между двумя простыми корнями составляет 120 °.
, имеют правильный шестиугольный узор. Угол между двумя простыми корнями составляет 120 °.
12 корней Исключительная группа Ли G2, представленный Диаграмма Дынкина ![]()
![]()
![]() также имеют шестиугольную форму. Два простых корня двух длин имеют угол между собой 150 °.
также имеют шестиугольную форму. Два простых корня двух длин имеют угол между собой 150 °.
Рассечение
| 6-куб проекция | 12 рассечение ромба | |
|---|---|---|
 |  |  |
Coxeter заявляет, что каждый зоногон (а 2м-угольник, противоположные стороны которого параллельны и равной длины) можно разрезать на м(м-1) / 2 параллелограмма.[4]В частности, это верно для правильные многоугольники с равным числом сторон, в этом случае все параллелограммы ромбовидны. Это разложение правильного шестиугольника основано на Многоугольник Петри проекция куб, с 3 из 6 квадратных граней. Другой параллелогоны и проективные направления куба рассекаются внутри прямоугольные кубоиды.
| Разрезание шестиугольников на три ромба и параллелограммы | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2D | Ромбы | Параллелограммы | |||||||||
 |  |  |  | ||||||||
| Обычный {6} | Шестиугольный параллелогоны | ||||||||||
| 3D | Квадратные лица | Прямоугольные грани | |||||||||
 |  |  |  | ||||||||
| Куб | Прямоугольный кубоид | ||||||||||
Связанные полигоны и мозаики
Правильный шестиугольник имеет Символ Шлефли {6}. Правильный шестиугольник входит в состав правильного шестиугольная черепица, {6,3}, с тремя шестиугольными гранями вокруг каждой вершины.
Правильный шестиугольник также можно создать как усеченный равносторонний треугольник, с символом Шлефли t {3}. Если смотреть с двумя типами (цветами) кромок, эта форма имеет только D3 симметрия.
А усеченный шестиугольник, t {6}, является двенадцатигранник, {12}, чередование двух типов (цветов) кромок. An чередовались шестиугольник, h {6}, является равносторонний треугольник, {3}. Правильный шестиугольник можно звездчатый с равносторонними треугольниками по краям, создавая гексаграмма. Правильный шестиугольник можно разрезать на шесть равносторонние треугольники добавив центральную точку. Этот шаблон повторяется в обычном треугольная черепица.
Правильный шестиугольник можно продолжить до правильного двенадцатигранник добавляя чередующиеся квадраты и равносторонние треугольники вокруг него. Этот шаблон повторяется в ромбитогексагональная черепица.
 |  |  |  |  |  |  |  |
| Обычный {6} | Усеченный t {3} = {6} | Гипертрофированные треугольники | Звездчатый Фигура звезды 2{3} | Усеченный т {6} = {12} | Альтернативный ч {6} = {3} | ||
|---|---|---|---|---|---|---|---|
 |  |  |  | 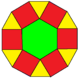 | 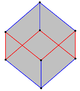 |
| Скрещенный шестиугольник | Вогнутый шестиугольник | Самопересекающийся шестиугольник (звездный многоугольник ) | Рассеченный {6} | Расширенный Центр {6} в {12} | А косой шестиугольник, в пределах куб |
|---|
Шесть самопересекающиеся шестиугольники с расположение вершин правильного шестиугольника:
| Dih2 | Dih1 | Dih3 | |||
|---|---|---|---|---|---|
 Восьмерка |  Центр-флип |  Unicursal |  Рыбий хвост |  Двойной хвост | 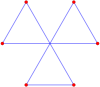 Тройной хвост |
Гексагональные конструкции

Из пчелиного соты к Дорога гигантов, гексагональные узоры преобладают в природе благодаря своей эффективности. В шестиугольная сетка каждая линия должна быть настолько короткой, насколько это возможно, если большая область должна быть заполнена наименьшим количеством шестиугольников. Это означает, что соты требуют меньше воск построить и набраться сил под сжатие.
Неправильные шестиугольники с параллельными противоположными краями называются параллелогоны а также может выложить плоскость по переводу. В трех измерениях, шестиугольные призмы с параллельными противоположными гранями называются параллелоэдры и они могут мозаику 3-пространства путем перевода.
| Форма | Шестиугольная черепица | Гексагональные призматические соты |
|---|---|---|
| Обычный |  |  |
| Параллелогональный |  |  |
Месселяция шестиугольниками
В дополнение к правильному шестиугольнику, который определяет уникальную мозаику плоскости, любой неправильный шестиугольник, удовлетворяющий Критерий Конвея выложит плоскость плиткой.
Шестиугольник, вписанный в коническое сечение
Теорема Паскаля (также известная как «Теорема Hexagrammum Mysticum») утверждает, что если произвольный шестиугольник вписан в любой коническая секция, и пары противоположных стороны расширены пока они не встретятся, три точки пересечения будут лежать на прямой линии, «линии Паскаля» этой конфигурации.
Циклический шестиугольник
В Лемуан шестиугольник это циклический шестиугольник (вписанный в круг) с вершинами, заданными шестью пересечениями ребер треугольника и тремя линиями, параллельными ребрам, проходящим через его симедианная точка.
Если последовательные стороны циклического шестиугольника равны а, б, c, d, е, ж, то три главные диагонали пересекаются в одной точке тогда и только тогда, когда туз = bdf.[5]
Если для каждой стороны циклического шестиугольника смежные стороны продолжаются до их пересечения, образуя треугольник, внешний по отношению к данной стороне, то отрезки, соединяющие центры описанных окружностей противоположных треугольников, равны одновременный.[6]
Если шестиугольник имеет вершины на описанный круг из острый треугольник в шести точках (включая три вершины треугольника), где расширенные высоты треугольника пересекаются с описанной окружностью, площадь шестиугольника в два раза больше площади треугольника.[7]:п. 179
Шестиугольник, касательный к коническому сечению
Пусть ABCDEF - шестиугольник, образованный шестью касательные линии конического сечения. потом Теорема Брианшона утверждает, что три главных диагонали AD, BE и CF пересекаются в одной точке.
В шестиугольнике по касательной к окружности и у этого есть последовательные стороны а, б, c, d, е, и ж,[8]
Равносторонние треугольники по сторонам произвольного шестиугольника

Если равносторонний треугольник строится снаружи с каждой стороны любого шестиугольника, тогда середины отрезков, соединяющих центроиды из противоположных треугольников образуют другой равносторонний треугольник.[9]:Thm. 1
Наклоненный шестиугольник

А косой шестиугольник это наклонный многоугольник с шестью вершинами и ребрами, но не в одной плоскости. Внутренняя часть такого шестиугольника обычно не определяется. А косой зигзагообразный шестиугольник имеет чередующиеся вершины между двумя параллельными плоскостями.
А правильный косой шестиугольник является вершинно-транзитивный с равной длиной кромки. В трех измерениях это будет зигзагообразный косой шестиугольник, который можно увидеть в вершинах и боковых краях треугольная антипризма с тем же D3D, [2+, 6] симметрия, порядок 12.
В куб и октаэдр (как и треугольная антипризма) имеют правильные скошенные шестиугольники как многоугольники Петри.
 Куб | 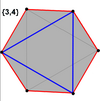 Октаэдр |
Полигоны Петри
Правильный косой шестиугольник - это Многоугольник Петри для этих высших измерений регулярный, равномерные и двойственные многогранники и многогранники, показанные в этих косых ортогональные проекции:
| 4D | 5D | |
|---|---|---|
 3-3 дуопризма | 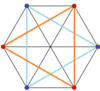 3-3 дуопирамида |  5-симплекс |
Выпуклый равносторонний шестиугольник
А главная диагональ шестиугольника - это диагональ, которая делит шестиугольник на четырехугольники. В любом выпуклом равносторонний шестиугольник (один со всеми равными сторонами) с общей стороной а, Существует[10]:стр.184, № 286.3 главная диагональ d1 такой, что
и главная диагональ d2 такой, что
Многогранники с шестиугольниками
Здесь нет Платоново твердое тело состоит только из правильных шестиугольников, потому что шестиугольники мозаика, не позволяя результату «свернуться». В Архимедовы тела с некоторыми шестиугольными гранями усеченный тетраэдр, усеченный октаэдр, усеченный икосаэдр (из футбольный мяч и фуллерен слава), усеченный кубооктаэдр и усеченный икосододекаэдр. Эти шестиугольники можно считать усеченный треугольники, с Диаграммы Кокстера формы ![]()
![]()
![]()
![]()
![]() и
и ![]()
![]()
![]()
![]()
![]() .
.
| Шестиугольники в Архимедовы тела | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Тетраэдр | Восьмигранный | Икосаэдр | |||||||||
 усеченный тетраэдр |  усеченный октаэдр |  усеченный кубооктаэдр |  усеченный икосаэдр |  усеченный икосододекаэдр | |||||||
Существуют и другие многогранники симметрии с вытянутыми или уплощенными шестиугольниками, например эти. Многогранник Гольдберга G (2,0):
| Шестиугольники в многогранниках Гольдберга | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Тетраэдр | Восьмигранный | Икосаэдр | |||||||||
 Тетраэдр с фаской |  Куб с фаской |  Додекаэдр с фаской | |||||||||
Также есть 9 Твердые тела Джонсона с правильными шестиугольниками:
| Призмоиды с шестиугольниками | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
 Гексагональная призма |  Шестиугольная антипризма |  Гексагональная пирамида | |||||||||
| Плитки с правильными шестиугольниками | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Обычный | 1-униформа | ||||||||||
| {6,3} | г {6,3} | рр {6,3} | tr {6,3} | ||||||||
 |  |  |  | ||||||||
| 2-однородные мозаики | |||||||||||
 |  |  |  | ||||||||
Галерея натуральных и искусственных шестиугольников

Идеальная кристаллическая структура графен представляет собой гексагональную сетку.

Собранный E-ELT зеркальные сегменты

Улей соты

Щитки черепахи панцирь

Шестиугольник Сатурна, гексагональный узор облаков вокруг северного полюса планеты

Микрофотография снежинки

Бензол, простейший ароматическое соединение с шестиугольной формой.

Шестиугольный порядок пузырьков в пене.

Кристаллическая структура молекулярный шестиугольник состоит из гексагональных ароматических колец.

Естественно сформированный базальт столбцы из Дорога гигантов в Северная Ирландия; большие массы должны медленно остывать, чтобы образовалась полигональная структура трещин

Вид с воздуха на Форт Джефферсон в Национальный парк Драй Тортугас

В Космический телескоп Джеймса Уэбба зеркало состоит из 18 шестиугольных сегментов.

Метрополитен Франция имеет неопределенно шестиугольную форму. На французском, l'Hexagone относится к европейской части Франции.
Шестиугольный Hanksite кристалл, один из многих гексагональная кристаллическая система минералы

Шестиугольный сарай

Шестиугольник, шестиугольник театр в Ридинг, Беркшир

Владислава Глинского шестиугольные шахматы

Павильон в Тайвань ботанические сады
Смотрите также
- 24-элементный: а четырехмерный фигура, которая, как и шестиугольник, имеет ортоплекс грани, это самодвойственный и мозаики Евклидово пространство
- Гексагональная кристаллическая система
- Шестиугольное число
- Шестиугольная черепица: а обычная черепица шестиугольников в плоскости
- Гексаграмма: шестигранная звезда в правильном шестиугольнике
- Уникурсальная гексаграмма: одинарный путь, шестигранная звезда, внутри шестиугольника
- Гипотеза о сотах
- Гаванна: абстрактная настольная игра на шестигранной гексагональной сетке
использованная литература
- ^ Веннингер, Магнус Дж. (1974), Модели многогранников, Cambridge University Press, стр. 9, ISBN 9780521098595, в архиве из оригинала на 02.01.2016, получено 2015-11-06.
- ^ а б Месхишвили, Мамука (2020). «Средние циклические правильные многоугольники и платоновы тела». Коммуникации в математике и приложениях. 11: 335–355.
- ^ Джон Х. Конвей, Хайди Берджел, Хаим Гудман-Штраус, (2008) Симметрии вещей, ISBN 978-1-56881-220-5 (Глава 20, Обобщенные символы Шафли, Типы симметрии многоугольника, стр. 275-278)
- ^ Coxeter, Математические развлечения и эссе, тринадцатое издание, с.141
- ^ Картенсен, Йенс, «О шестиугольниках», Математический спектр 33(2) (2000–2001), 37–40.
- ^ Дергиадес, Николаос (2014). «Теорема Дао о шести центрах окружности, связанных с циклическим шестиугольником». Форум Geometricorum. 14: 243–246. В архиве из оригинала от 05.12.2014. Получено 2014-11-17.
- ^ Джонсон, Роджер А., Продвинутая евклидова геометрия, Dover Publications, 2007 (начало 1960 г.).
- ^ Гутьеррес, Антонио, «Шестиугольник, начертанный круг, касательная, полупериметр», [1] В архиве 2012-05-11 в Wayback Machine, Проверено 17 апреля 2012 г.
- ^ Дао Тхань Оай (2015). «Равносторонние треугольники и перспективы Киперта в комплексных числах». Форум Geometricorum. 15: 105–114. В архиве из оригинала от 05.07.2015. Получено 2015-04-12.
- ^ Неравенства, предложенные в «Crux Mathematicorum ”, [2] В архиве 2017-08-30 в Wayback Machine.
внешние ссылки
Эта статья использование внешние ссылки может не следовать политикам или рекомендациям Википедии. (Ноябрь 2017 г.) (Узнайте, как и когда удалить этот шаблон сообщения) |
- Определение и свойства шестиугольника с интерактивной анимацией и конструкция с циркулем и линейкой.
- Введение в гексагональную геометрию на Hexnet сайт, посвященный математике шестиугольника.
- Кассини изображает причудливый шестиугольник на Сатурне
- Странный шестиугольник Сатурна
- Шестиугольная деталь вокруг Северного полюса Сатурна
- "На Сатурне замечен странный шестиугольник" - от Space.com (27 марта 2007 г.)