G2 (математика) - G2 (mathematics)
| Алгебраическая структура → Теория групп Теория групп |
|---|
 |
Бесконечномерная группа Ли
|
| Группы Ли |
|---|
 |
|
В математика, грамм2 это имя трех простых Группы Ли (сложная форма, компактная реальная форма и раздельная реальная форма), их Алгебры Ли а также некоторые алгебраические группы. Они самые маленькие из пяти исключительных простые группы Ли. грамм2 имеет ранг 2 и размерность 14. Имеет два фундаментальные представления, размерностью 7 и 14.
Компактная форма G2 можно описать как группа автоморфизмов из октонионная алгебра или, что то же самое, как подгруппа SO (7), которая сохраняет любой выбранный конкретный вектор в его 8-мерном настоящий спинор представление (а представление вращения ).
История
Алгебра Ли , будучи наименьшей исключительной простой алгеброй Ли, была первой из них, обнаруженной при попытке классификации простых алгебр Ли. 23 мая 1887 г. Вильгельм Киллинг написал письмо Фридрих Энгель говоря, что он нашел 14-мерную простую алгебру Ли, которую мы теперь называем .[1]
В 1893 г. Эли Картан опубликовал заметку, описывающую открытый сет в оснащен 2-х мерным распределение - то есть гладко меняющееся поле двумерных подпространств касательного пространства, для которого алгебра Ли появляется как бесконечно малые симметрии.[2] В том же году в том же журнале Энгель заметил то же самое. Позже было обнаружено, что двумерное распределение тесно связано с качением шара по другому шару. Пространство конфигураций катящегося шара является 5-мерным с двухмерным распределением, которое описывает движения шара, при котором он катится без проскальзывания или скручивания.[3][4]
В 1900 году Энгель обнаружил, что антисимметричная трилинейная форма (или 3-форма) общего вида на 7-мерном комплексном векторном пространстве сохраняется группой, изоморфной комплексной форме G2.[5]
В 1908 году Картан упомянул, что группа автоморфизмов октонионов является 14-мерной простой группой Ли.[6] В 1914 году он заявил, что это компактная вещественная форма G2.[7]
В старых книгах и статьях G2 иногда обозначается E2.
Реальные формы
С этой корневой системой связаны 3 простые вещественные алгебры Ли:
- Основная вещественная алгебра Ли комплексной алгебры Ли G2 имеет размерность 28. Он имеет комплексное сопряжение как внешний автоморфизм и односвязен. Максимальная компактная подгруппа ассоциированной с ней группы - это компактная форма группы G2.
- Алгебра Ли компактной формы 14-мерна. Ассоциированная группа Ли не имеет внешних автоморфизмов, центра, односвязна и компактна.
- Алгебра Ли некомпактной (расщепленной) формы имеет размерность 14. Ассоциированная простая группа Ли имеет фундаментальную группу порядка 2 и ее группа внешних автоморфизмов - тривиальная группа. Его максимальная компактная подгруппа равна SU (2) × SU (2) / (- 1, −1). Он имеет односвязное неалгебраическое двойное покрытие.
Алгебра
Диаграмма Дынкина и матрица Картана
В Диаграмма Дынкина за грамм2 дан кем-то ![]() .
.
Его Матрица Картана является:
Корни G2
 12 вектор корневая система из G2 в 2-х измерениях. | 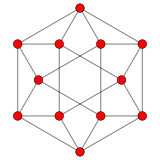 А2 Самолет Кокстера проекция 12 вершин кубооктаэдр содержат такое же расположение 2D-векторов. | 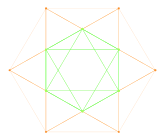 График G2 как подгруппы F4 и E8 в проекции на плоскость Кокстера |
Хотя они охватывать 2-мерное пространство, как оно нарисовано, гораздо более симметрично рассматривать как векторов в двумерном подпространстве трехмерного пространства.
|
|
Один комплект простые корни, за ![]()
![]()
![]() является:
является:
- (0,1,−1), (1,−2,1)
Группа Вейля / Кокстера
Его Weyl /Coxeter группа это группа диэдра, из порядок 12. Имеет минимальную степень верности. .
Специальная голономия
грамм2 одна из возможных специальных групп, которые могут появиться как голономия группа Риманова метрика. В коллекторы из G2 голономию также называют грамм2-многообразия.
Полиномиальный инвариант
грамм2 - группа автоморфизмов следующих двух многочленов от 7 некоммутативных переменных.
- (± перестановки)
которое происходит от алгебры октонионов. Переменные должны быть некоммутативными, иначе второй многочлен будет тождественно равен нулю.
Генераторы
Добавление представления 14 генераторов с коэффициентами А, ..., N дает матрицу:
Это в точности алгебра Ли группы
Представления
Характеры конечномерных представлений вещественных и комплексных алгебр Ли и групп Ли задаются Формула характера Вейля. Размерности наименьших неприводимых представлений равны (последовательность A104599 в OEIS ):
- 1, 7, 14, 27, 64, 77 (дважды), 182, 189, 273, 286, 378, 448, 714, 729, 748, 896, 924, 1254, 1547, 1728, 1729, 2079 (дважды), 2261, 2926, 3003, 3289, 3542, 4096, 4914, 4928 (дважды), 5005, 5103, 6630, 7293, 7371, 7722, 8372, 9177, 9660, 10206, 10556, 11571, 11648, 12096, 13090….
14-мерное представление - это присоединенное представительство, а 7-мерное - действие группы G2 на мнимых октонионах.
Имеются два неизоморфных неприводимых представления размерностей 77, 2079, 4928, 28652 и т. Д. фундаментальные представления имеют размеры 14 и 7 (соответствующие двум узлам в Диаграмма Дынкина в таком порядке, чтобы тройная стрелка указывала от первой ко второй).
Воган (1994) описал (бесконечномерные) унитарные неприводимые представления расщепленной вещественной формы G2.
Конечные группы
Группа G2(q) - точки алгебраической группы G2 над конечное поле Fq. Эти конечные группы были впервые введены Леонард Юджин Диксон в Диксон (1901) для нечетных q и Диксон (1905) даже для q. Порядок G2(q) является q6(q6 − 1)(q2 − 1). Когда q ≠ 2, группа просто, и когда q = 2, он имеет простую подгруппу индекс 2 изоморфен 2А2(32), - группа автоморфизмов максимального порядка октонионов. Группа Янко J1 была впервые построена как подгруппа в G2(11). Ри (1960) представил скрученный Ри группы 2грамм2(q) порядка q3(q3 + 1)(q − 1) за q = 32п+1, нечетная степень 3.
Смотрите также
- Матрица Картана
- Диаграмма Дынкина
- Исключительная йорданова алгебра
- Фундаментальное представление
- грамм2-структура
- Группа Ли
- Семимерное перекрестное произведение
- Простая группа Ли
Рекомендации
- ^ Агрикола, Илька (2008). "Старые и новые в исключительной группе грамм2" (PDF). Уведомления Американского математического общества. 55 (8): 922–929. МИСТЕР 2441524.
- ^ Эли Картан (1893 г.). «Sur la structure des groupes simples finis et continus». C. R. Acad. Наука. 116: 784–786.
- ^ Гил Бор и Ричард Монтгомери (2009). "ГРАММ2 и "прокатное распределение"". L'Enseignement Mathématique. 55: 157–196. arXiv:математика / 0612469. Дои:10.4171 / lem / 55-1-8.
- ^ Джон Баэз и Джон Уэрта (2014). "ГРАММ2 и катящийся шар ". Пер. Амер. Математика. Soc. 366 (10): 5257–5293. arXiv:1205.2447. Дои:10.1090 / s0002-9947-2014-05977-1.
- ^ Фридрих Энгель (1900). "Ein neues, dem linearen Komplexe аналоги Gebilde". Лейпц. Ber. 52: 63–76, 220–239.
- ^ Эли Картан (1908). «Комплексы Номбре». Энциклопедия математических наук. Париж: Готье-Виллар. С. 329–468.
- ^ Эли Картан (1914), "Les groupes reels simples finis et continus", Анна. Sci. École Norm. Как дела., 31: 255–262
- Адамс, Дж. Франк (1996), Лекции об исключительных группах Ли, Чикагские лекции по математике, Издательство Чикагского университета, ISBN 978-0-226-00526-3, МИСТЕР 1428422
- Баэз, Джон (2002), «Октонионы», Бык. Амер. Математика. Soc., 39 (2): 145–205, arXiv:математика / 0105155, Дои:10.1090 / S0273-0979-01-00934-X.
- См. Раздел 4.1: G2; онлайн-версия HTML доступна по адресу http://math.ucr.edu/home/baez/octonions/node14.html.
- Брайант, Роберт (1987), «Метрики с исключительной голономией», Анналы математики, 2, 126 (3): 525–576, Дои:10.2307/1971360, JSTOR 1971360
- Диксон, Леонард Юджин (1901), "Теория линейных групп в произвольном поле", Труды Американского математического общества, Провиденс, Р.И.: Американское математическое общество, 2 (4): 363–394, Дои:10.1090 / S0002-9947-1901-1500573-3, ISSN 0002-9947, JSTOR 1986251, Перепечатанный в томе II его собрания статей Леонард Э. Диксон сообщил о группах типа G2 в полях нечетной характеристики.
- Диксон, Л.Э. (1905), «Новая система простых групп», Математика. Анна., 60: 137–150, Дои:10.1007 / BF01447497 Леонард Э. Диксон сообщил о группах типа G2 в полях четной характеристики.
- Ри, Римхак (1960), "Семейство простых групп, связанных с простой алгеброй Ли типа (G2)", Бюллетень Американского математического общества, 66 (6): 508–510, Дои:10.1090 / S0002-9904-1960-10523-X, ISSN 0002-9904, МИСТЕР 0125155
- Воган, Дэвид А. младший (1994), "Унитарный двойственный G2", Inventiones Mathematicae, 116 (1): 677–791, Bibcode:1994ИнМат.116..677В, Дои:10.1007 / BF01231578, ISSN 0020-9910, МИСТЕР 1253210




![{ displaystyle left [{ begin {array} {rr} 2 & -3 - 1 & 2 end {array}} right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/37b6638e3fd0ff7eab3058d40fed0f592c94dbf4)







