Группа Quaternion - Quaternion group
| Алгебраическая структура → Теория групп Теория групп |
|---|
 |
Бесконечномерная группа Ли
|

В теория групп, то группа кватернионов Q8 (иногда обозначается просто Q) является неабелев группа из порядок восемь, изоморфное восьмиэлементному подмножеству из кватернионы при умножении. Это дано групповая презентация
где e - единичный элемент и е ездит на работу с другими элементами группы.
Другая представление Q8 является:
По сравнению с диэдральной группой
Группа кватернионов Q8 имеет тот же порядок, что и группа диэдра D4, но с другой структурой, как показано на их графиках Кэли и циклов:
| Q8 | D4 | |
|---|---|---|
| Граф Кэли | 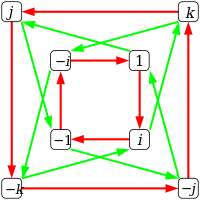 Красные стрелки соединяют г→джи, зеленый подключить г→gj. |  |
| График цикла | 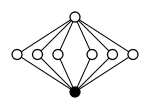 |  |
На диаграммах для D4, элементы группы помечаются своим действием на букву F в определяющем представлении р2. То же самое нельзя сделать для Q8, поскольку он не имеет точного представления в р2 или р3. D4 может быть реализована как подмножество расщепленные кватернионы так же, как Q8 можно рассматривать как подмножество кватернионов.
Стол Кэли
В Стол Кэли (таблица умножения) для Q8 дан кем-то:[1]
| × | е | е | я | я | j | j | k | k |
|---|---|---|---|---|---|---|---|---|
| е | е | е | я | я | j | j | k | k |
| е | е | е | я | я | j | j | k | k |
| я | я | я | е | е | k | k | j | j |
| я | я | я | е | е | k | k | j | j |
| j | j | j | k | k | е | е | я | я |
| j | j | j | k | k | е | е | я | я |
| k | k | k | j | j | я | я | е | е |
| k | k | k | j | j | я | я | е | е |
Свойства
Обратите внимание, что я, j, и k у всех есть порядок четыре в Q8 и любые два из них создают всю группу. Другая презентация из Q8[2] демонстрируя это:
Можно взять, например, , и .
Группа кватернионов обладает необычным свойством быть Гамильтониан: Q8 неабелева, но каждый подгруппа является нормальный.[3] Каждая гамильтонова группа содержит копию Q8.[4]
Группа кватернионов Q8 и диэдральная группа D4 два самых маленьких примера нильпотентный неабелева группа.
В центр и коммутаторная подгруппа из Q8 это подгруппа . В группа внутренних автоморфизмов из Q8 задается группой по модулю ее центра, т. е. факторная группа Q8/ {е,е}, который изоморфный к Кляйн четыре группы V. Полная группа автоморфизмов из Q8 является изоморфный к S4, то симметричная группа на четырех буквах (см. Матричные представления ниже), а группа внешних автоморфизмов из Q8 таким образом, S4/ V, который изоморфен S3.
Группа кватернионов Q8 имеет пять классов сопряженности, {e}, { е }, {i, я }, {j, j }, {k, k }, так что пять неприводимые представления над комплексными числами с размерностями 1,1,1,1,2:
Тривиальное представление
Знаковые представления с i, j, k-ядром: Q8 имеет три максимальные нормальные подгруппы: циклические подгруппы, порожденные i, j и k соответственно. Для каждой максимальной нормальной подгруппы N, получим одномерное представление факторизуя через 2-элементную факторгруппа г/N. Представление отправляет элементы N до 1, а элементы вне N до -1.
2-мерное представление: Описано ниже в Матричные представления.
В таблица символов из Q8 оказывается таким же, как у D4:
| Представление (ρ) / Класс сопряженности | {e} | { е } | {я, я } | {j, j } | {k, k } |
|---|---|---|---|---|---|
| Тривиальное представление | 1 | 1 | 1 | 1 | 1 |
| Знаковое представление с i-ядром | 1 | 1 | 1 | -1 | -1 |
| Знаковое представление с j-ядром | 1 | 1 | -1 | 1 | -1 |
| Знаковое представление с k-ядром | 1 | 1 | -1 | -1 | 1 |
| 2-мерное представление | 2 | -2 | 0 | 0 | 0 |
Поскольку неприводимые персонажи в строках выше имеют реальные значения, это дает разложение настоящих групповая алгебра из на минимальный двусторонний идеалы: , где идемпотенты соответствуют неприводимым: , так что
.
Каждый из этих неприводимых идеалов изоморфен вещественному центральная простая алгебра, первые четыре к реальному полю . Последний идеал изоморфен тело из кватернионы по переписке:
Кроме того, гомоморфизм проекций данный имеет идеал ядра, порожденный идемпотентом:
поэтому кватернионы также могут быть получены как кольцо частного .
Таким образом, комплексная групповая алгебра , где это алгебра бикватернионы.
Матричные представления
Двумерный неприводимый комплекс представление описанное выше дает кватернионную группу Q8 как подгруппа общая линейная группа . Группа кватернионов является мультипликативной подгруппой алгебры кватернионов , который имеет регулярное представительство умножением слева на себя, рассматриваемого как комплексное векторное пространство с базой , так что соответствует C-линейное отображение . Полученное представление дан кем-то:
Поскольку все указанные выше матрицы имеют единичный определитель, это представление Q8 в специальная линейная группа SL2(C).[5]
Вариант дает представление унитарные матрицы (таблица справа). Позволять соответствуют линейному отображению , так что дан кем-то:

Также есть важное действие Q8 на двумерном векторном пространстве над конечное поле F3 = {0,1, −1} (таблица справа). А модульное представление дан кем-то
Это представление можно получить из поле расширения F9 = F3[k] = F31 + F3k, где k2 = −1 и мультипликативная группа (F9)× имеет образующие ± (k+1), ±(k-1) порядка 8. Двумерный F3-векторное пространство F9 допускает линейные отображения для z в F9, так же хорошо как Автоморфизм Фробениуса удовлетворение и . Тогда указанные выше матрицы представления равны , , , и .
Приведенное выше представление реализует Q8 как нормальная подгруппа из GL (2, 3). Таким образом, для каждой матрицы , имеем групповой автоморфизм определяется , с участием . Фактически, они дают полную группу автоморфизмов как:
,
Это изоморфно симметрической группе S4 поскольку линейные отображения переставить четыре одномерных подпространства , т.е. четыре точки проективное пространство .
Кроме того, это представление переставляет восемь ненулевых векторов (F3)2, дающее вложение Q8 в симметричная группа S8, в дополнение к вложениям, задаваемым регулярными представлениями.
Группа Галуа
Как показал Ричард Дин в 1981 году, кватернионную группу можно представить как Группа Галуа Гал (т /Q) где Q это область рациональное число а T - поле расщепления над Q полинома
- .
В разработке используется основная теорема теории Галуа в указании четырех промежуточных полей между Q и T и их группы Галуа, а также две теоремы о циклическом расширении степени четыре над полем.[6]
Обобщенная группа кватернионов
А обобщенная группа кватернионов Q4п порядка 4п определяется презентацией[2]
для целого числа п ≥ 2, с обычной группой кватернионов, заданной п = 2.[7] Coxeter называет Q4п то дициклическая группа , частный случай бинарная группа полиэдров и связанные с группа полиэдров и группа диэдра . Обобщенная группа кватернионов может быть реализована как подгруппа Сгенерированно с помощью
где .[2] Он также может быть реализован как подгруппа единичных кватернионов, порожденная[8] и .
Обобщенные группы кватернионов обладают тем свойством, что каждые абелевский подгруппа циклическая.[9] Можно показать, что конечная п-группа с этим свойством (каждая абелева подгруппа циклическая) является либо циклической, либо обобщенной кватернионной группой, как определено выше.[10] Другая характеристика состоит в том, что конечное п-группа, в которой существует единственная подгруппа порядка п является либо циклической, либо 2-группой, изоморфной обобщенной группе кватернионов.[11] В частности, для конечного поля F с нечетной характеристикой 2-силовская подгруппа группы SL2(F) неабелева и имеет только одну подгруппу порядка 2, поэтому эта 2-силовская подгруппа должна быть обобщенной группой кватернионов, (Горенштейн 1980, п. 42). Сдача пр быть размером с F, где п простое число, размер 2-силовской подгруппы группы SL2(F) равно 2п, где п = ord2(п2 - 1) + ord2(р).
В Теорема Брауэра – Судзуки показывает, что группы, силовские 2-подгруппы которых являются обобщенным кватернионом, не могут быть простыми.
Другая терминология резервирует название «обобщенная группа кватернионов» для дициклической группы порядка степени двойки,[12] который допускает представление
Смотрите также
- 16 ячеек
- Бинарная тетраэдрическая группа
- Алгебра Клиффорда
- Дициклическая группа
- Интегральный кватернион Гурвица
- Список малых групп
Заметки
- ^ Смотрите также стол от вольфрам Альфа
- ^ а б c Джонсон 1980, стр. 44–45
- ^ См. Холл (1999), п. 190
- ^ См. Kurosh (1979), п. 67
- ^ Артин 1991
- ^ Дин, Ричард (1981). «Рациональный многочлен, группа которого - кватернионы». Американский математический ежемесячник. 88 (1): 42–45. JSTOR 2320711.
- ^ Некоторые авторы (например, Ротман 1995, pp. 87, 351) называют эту группу дициклической группой, оставляя название обобщенная группа кватернионов для случая, когда п это степень двойки.
- ^ Коричневый 1982, п. 98
- ^ Коричневый 1982, п. 101, упражнение 1
- ^ Картан и Эйленберг, 1999 г., Теорема 11.6, с. 262
- ^ Коричневый 1982, Теорема 4.3, с. 99
- ^ Роман, Стивен (2011). Основы теории групп: продвинутый подход. Springer. С. 347–348. ISBN 9780817683016.
использованная литература
- Артин, Майкл (1991), Алгебра, Прентис Холл, ISBN 978-0-13-004763-2
- Браун, Кеннет С. (1982), Когомологии групп (3-е изд.), Springer-Verlag, ISBN 978-0-387-90688-1
- Картан, Анри; Эйленберг, Самуэль (1999), Гомологическая алгебра, Издательство Принстонского университета, ISBN 978-0-691-04991-5
- Кокстер, Х. С. М. И Мозер, В. О. Дж. (1980). Генераторы и соотношения для дискретных групп. Нью-Йорк: Springer-Verlag. ISBN 0-387-09212-9.
- Дин, Ричард А. (1981) "Рациональный многочлен, группа которого - кватернионы", Американский математический ежемесячный журнал 88:42–5.
- Горенштейн, Д. (1980), Конечные группы, Нью-Йорк: Челси, ISBN 978-0-8284-0301-6, Г-Н 0569209
- Джонсон, Дэвид Л. (1980), Темы теории групповых представлений, Издательство Кембриджского университета, ISBN 978-0-521-23108-4, Г-Н 0695161
- Ротман, Джозеф Дж. (1995), Введение в теорию групп (4-е изд.), Springer-Verlag, ISBN 978-0-387-94285-8
- П. Р. Жирар (1984) "Группа кватернионов и современная физика", Европейский журнал физики 5:25–32.
- Холл, Маршалл (1999), Теория групп (2-е изд.), Книжный магазин AMS, ISBN 0-8218-1967-4
- Курош Александр Г. (1979), Теория групп, Книжный магазин AMS, ISBN 0-8284-0107-1
внешние ссылки
- Вайсштейн, Эрик В. «Кватернион группа». MathWorld.
- Группы кватернионов в GroupNames
- Группа Quaternion на GroupProps
- Конрад, Кит. «Обобщенные кватернионы»










![{ Displaystyle textstyle mathbb {R} [Q_ {8}] = bigoplus _ { rho} (е _ { rho})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1761120670b220c341d6011a5828e02fbea91465)
![{ Displaystyle е _ { rho} in mathbb {R} [Q_ {8}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/998bce07bcab28516257658681275cfa3fa3565d)










![{ Displaystyle mathbb {R} [Q_ {8}] to (e_ {2}) cong mathbb {H}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ed575d6fe2a2f4ad1b041497334d7e11f32fe5a3)


![{ Displaystyle mathbb {R} [Q_ {8}] / (е + { бар {е}}) cong mathbb {H}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/53ab95cc1e1943df7e6665e199487fb543252663)
![{ Displaystyle mathbb {C} [Q_ {8}] cong mathbb {C} ^ { oplus 4} oplus M_ {2} ( mathbb {C})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/86853166cd0baf213603720e72f18b1175ae519d)










































