Чередующаяся группа - Alternating group

Эта статья включает в себя список общих использованная литература, но он остается в основном непроверенным, потому что ему не хватает соответствующих встроенные цитаты. Пожалуйста, помогите улучшить эта статья введение более точные цитаты. (Январь 2008 г.) (Узнайте, как и когда удалить этот шаблон сообщения)

Алгебраическая структура → Теория групп Теория групп
Основные понятия Подгруппа Нормальная подгруппа Факторная группа (Полу-)прямой продукт Групповые гомоморфизмы ядро образ прямая сумма венок просто конечный бесконечный непрерывный мультипликативный добавка циклический абелевский двугранный нильпотентный разрешимый Глоссарий теории групп Список тем теории групп
Конечные группы Классификация конечных простых групп циклический чередование Тип лжи спорадический Теорема Коши Теорема Лагранжа Теоремы Силова Теорема холла p-группа Элементарная абелева группа Группа Фробениуса Множитель Шура Симметричная группа Sп Кляйн четыре группы V Группа диэдра Dп Группа Quaternion Q Дициклическая группа Dicп
Дискретные группы Решетки Целые числа (Z) Бесплатная группа Модульные группы PSL (2,Z) SL (2,Z) Арифметическая группа Решетка Гиперболическая группа
Топологический и Группы Ли Соленоид Круг Общие линейные GL (п) Специальная линейная SL (п) Ортогональный O (п) Евклидово E (п) Специальные ортогональные ТАК(п) Унитарный U (п) Специальный унитарный SU (п) Симплектический Sp (п) г2 F4 E6 E7 E8 Лоренц Пуанкаре Конформный Диффеоморфизм Петля Бесконечномерная группа Ли O (∞) SU (∞) Sp (∞)
Алгебраические группы Линейная алгебраическая группа Редуктивная группа Абелева разновидность Эллиптическая кривая

В математика, переменная группа это группа из даже перестановки из конечный набор. Переменная группа на множестве п элементы называется переменная группа степеней п, или чередующаяся группа на п письма и обозначается A_п или Alt (п).

Основные свойства

Для п > 1, группа A_п это коммутаторная подгруппа из симметричная группа S_п с участием показатель 2 и поэтому п! / 2 элемента. Это ядро подписи групповой гомоморфизм sgn: S_п → {1, −1} объяснено под симметричная группа.

Группа А_п является абелевский если и только если п ≤ 3 и просто если и только если п = 3 или п ≥ 5. А₅ наименьший неабелев простая группа, имеющий порядок 60, а наименьшее не-разрешимая группа.

Группа А₄ имеет Кляйн четыре группы V как собственно нормальная подгруппа, а именно тождество и двойные транспозиции { (), (12)(34), (13)(24), (14)(23) }, это ядро ​​сюръекции A₄ на А₃ = C₃. У нас есть точная последовательность V → A₄ → А₃ = C₃. В Теория Галуа, эта карта, а точнее соответствующая карта S₄ → S₃, соответствует связыванию Резольвента Лагранжа кубическая в квартику, что позволяет полином четвертой степени решаться радикалами, как установлено Лодовико Феррари.

Классы сопряженности

Как в симметричная группа, любые два элемента из A_п которые сопряжены элементом A_п должно быть то же самое форма цикла. Однако обратное не всегда верно. Если форма цикла состоит только из циклов нечетной длины без двух циклов одинаковой длины, где циклы длины один включены в тип цикла, то для этой формы цикла существует ровно два класса сопряженности (Скотт 1987, §11.1, стр.299).

Примеры:

• Два перестановки (123) и (132) не сопряжены в A₃, хотя они имеют одинаковую форму цикла и поэтому сопряжены в S₃.
• Перестановка (123) (45678) не сопряжена со своим обратным (132) (48765) в A₈, хотя две перестановки имеют одинаковую форму цикла, поэтому они сопряжены в S₈.

Связь с симметричной группой

Увидеть Симметричная группа.

Генераторы и отношения

А_п порождается 3-циклами, так как 3-циклы могут быть получены объединением пар транспозиций. Этот генератор часто используется для доказательства того, что A_п просто для п ≥ 5.

Группа автоморфизмов

${ displaystyle n}$	${ displaystyle operatorname {Aut} ( mathrm {A} _ {n})}$	${ displaystyle operatorname {Out} ( mathrm {A} _ {n})}$
${ Displaystyle п geq 4, п neq 6}$	${ displaystyle mathrm {S} _ {n}}$	${ displaystyle mathrm {Z} _ {2}}$
${ displaystyle n = 1,2}$	${ displaystyle mathrm {Z} _ {1}}$	${ displaystyle mathrm {Z} _ {1}}$
${ displaystyle n = 3}$	${ displaystyle mathrm {Z} _ {2}}$	${ displaystyle mathrm {Z} _ {2}}$
${ displaystyle n = 6}$	${ Displaystyle mathrm {S} _ {6} rtimes mathrm {Z} _ {2}}$	${ Displaystyle mathrm {V} = mathrm {Z} _ {2} times mathrm {Z} _ {2}}$

Для п > 3, кроме п = 6, то группа автоморфизмов из А_п симметрическая группа S_п, с участием группа внутренних автоморфизмов А_п и группа внешних автоморфизмов Z₂; внешний автоморфизм происходит от сопряжения нечетной перестановкой.

Для п = 1 и 2, группа автоморфизмов тривиальна. Для п = 3 группа автоморфизмов Z₂, с тривиальной группой внутренних автоморфизмов и группой внешних автоморфизмов Z₂.

Группа внешних автоморфизмов A₆ является четыре группы Клейна V = Z₂ × Z₂, и связан с внешний автоморфизм S₆. Дополнительный внешний автоморфизм в A₆ меняет местами 3-циклы (например, (123)) с элементами формы 3² (как (123) (456)).

Исключительные изоморфизмы

Есть некоторые исключительные изоморфизмы между небольшими чередующимися группами и небольшими группы лиева типа особенно проективные специальные линейные группы. Эти:

• А₄ изоморфен PSL₂(3)^[1] и группа симметрии хирального тетраэдрическая симметрия.
• А₅ изоморфен PSL₂(4), PSL₂(5), а группа симметрии киральных икосаэдрическая симметрия. (Увидеть^[1] для косвенного изоморфизма PSL₂(F₅) → А₅ используя классификацию простых групп порядка 60, и Вот для прямого доказательства).
• А₆ изоморфен PSL₂(9) и PSp₄(2)'.
• А₈ изоморфен PSL₄(2).

Более очевидно, что A₃ изоморфен циклическая группа Z₃, а А₀, А₁, а А₂ изоморфны тривиальная группа (который также SL₁(q) = PSL₁(q) для любого q).

Примеры S₄ и А₄

Стол Кэли из симметричная группа S4 В нечетные перестановки окрашены: Транспозиции в зеленом и 4 цикла в оранжевом

Таблица Кэли переменной группы А4 Элементы: четные перестановки (тождество, восемь 3 цикла и три двухместныхтранспозиции (двойные транспозиции жирным шрифтом)) Подгруппы:

Графики цикла

А3 = Z3 (заказ 3)	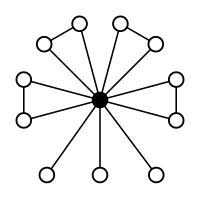А4 (заказ 12)	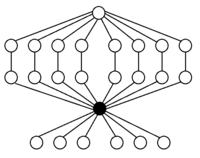А4 × Z2 (заказ 24)
S3 = Dih3 (заказ 6)	S4 (заказ 24)	А4 в S4 слева

Пример А₅ как подгруппа 3-пространственных вращений

${ Displaystyle A_ {5}$

  мяч - радиус π -принцип однородного пространства SO (3)

  икосододекаэдр - радиус π - класс сопряженности 2-2-циклов

  икосаэдр - радиус 4π/ 5 - половина Трещина класс сопряженности 5-циклов

  додекаэдр - радиус 2π/ 3 - класс сопряженности 3-циклов

  икосаэдр - радиус 2π/ 5 - половина секунд разделенных 5-циклов

Соединение пяти тетраэдров. ${ displaystyle A_ {5}}$ действует на додекаэдр, переставляя 5 вписанных тетраэдров. Даже перестановки этих тетраэдров являются в точности симметричными вращениями додекаэдра и характеризуют ${ Displaystyle A_ {5}$ переписка.

${ displaystyle A_ {5}}$ группа изометрий додекаэдра в 3-м пространстве, поэтому существует представление ${ Displaystyle A_ {5} к SO_ {3} ( mathbb {R})}$

На этом рисунке вершины многогранников представляют собой элементы группы, а центр сферы представляет собой единичный элемент. Каждая вершина представляет собой поворот вокруг оси, указывающей от центра к этой вершине, на угол, равный расстоянию от начала координат в радианах. Вершины одного многогранника принадлежат одному классу сопряженности. Поскольку уравнение класса сопряженности для ${ displaystyle A_ {5}}$ равно 1 + 12 + 12 + 15 + 20 = 60, получаем четыре различных (нетривиальных) многогранника.

Вершины каждого многогранника находятся в взаимно однозначном соответствии с элементами его класса сопряженности, за исключением класса сопряженности (2,2) -циклов, который представлен икосододекаэдром на внешней поверхности с его противоположными вершинами, отождествленными с друг друга. Причина этой избыточности в том, что соответствующие повороты выполняются ${ displaystyle pi}$ радиан, и поэтому может быть представлен вектором длины ${ displaystyle pi}$ в любом из двух направлений. Таким образом, класс (2,2) -циклов содержит 15 элементов, а икосододекаэдр имеет 30 вершин.

Два класса сопряженности двенадцати 5-циклов в ${ displaystyle A_ {5}}$ представлены двумя икосаэдрами радиусов ${ displaystyle 2 pi / 5}$ и ${ displaystyle 4 pi / 5}$соответственно. Нетривиальный внешний автоморфизм в ${ displaystyle { text {Out}} (A_ {5}) simeq Z_ {2}}$ меняет местами эти два класса и соответствующие икосаэдры.

Подгруппы

А₄ - наименьшая группа, демонстрирующая обратное Теорема Лагранжа в общем случае неверно: с учетом конечной группы г и делитель d из |г|, не обязательно существует подгруппа г с заказом d: группа г = А₄, порядка 12, не имеет подгруппы порядка 6. Подгруппа из трех элементов (порожденная циклическим вращением трех объектов) с любым отдельным нетривиальным элементом порождает всю группу.

Для всех п > 4, А_п не имеет нетривиальных (то есть собственных) нормальные подгруппы. Таким образом, A_п это простая группа для всех п > 4. А₅ самый маленький неразрешимая группа.

Групповая гомология

В групповая гомология чередующихся групп демонстрирует стабилизацию, как в теория стабильной гомотопии: для достаточно больших п, это постоянно. Однако есть некоторые исключительные гомологии малой размерности. Обратите внимание, что гомологии симметрической группы демонстрирует аналогичную стабилизацию, но без малоразмерных исключений (дополнительных элементов гомологии).

ЧАС₁: Абелианизация

Первый группа гомологии совпадает с абелианизация, и с тех пор ${ displaystyle mathrm {A} _ {n}}$ является идеально, за исключением указанных исключений) таким образом:

${ displaystyle H_ {1} ( mathrm {A} _ {n}, mathrm {Z}) = 0}$ для ${ Displaystyle п = 0,1,2}$;

${ displaystyle H_ {1} ( mathrm {A} _ {3}, mathrm {Z}) = mathrm {A} _ {3} ^ { text {ab}} = mathrm {A} _ { 3} = mathrm {Z} / 3}$;

${ Displaystyle H_ {1} ( mathrm {A} _ {4}, mathrm {Z}) = mathrm {A} _ {4} ^ { text {ab}} = mathrm {Z} / 3 }$;

${ displaystyle H_ {1} ( mathrm {A} _ {n}, mathrm {Z}) = 0}$ для ${ displaystyle n geq 5}$.

В этом легко убедиться напрямую, как в следующем. ${ displaystyle mathrm {A} _ {n}}$ порождается 3-циклами, поэтому единственными нетривиальными отображениями абелианизации являются ${ displaystyle mathrm {A} _ {n} to mathrm {C} _ {3},}$ поскольку элементы порядка 3 должны отображаться на элементы порядка 3 - и для ${ displaystyle n geq 5}$ все 3-циклы сопряжены, поэтому они должны отображаться в один и тот же элемент абелианизации, поскольку сопряжение тривиально в абелевых группах. Таким образом, 3-цикл, подобный (123), должен отображаться в тот же элемент, что и его обратный (321), но, таким образом, должен отображаться в тождество, так как тогда он должен иметь порядок деления 2 и 3, поэтому абелианизация тривиальна.

Для ${ Displaystyle п <3}$, ${ displaystyle mathrm {A} _ {n}}$ тривиально и, следовательно, имеет тривиальную абелианизацию. Для ${ displaystyle mathrm {A} _ {3}}$ и ${ displaystyle mathrm {A} _ {4}}$ можно вычислить абелианизацию напрямую, отметив, что 3-циклы образуют два класса сопряженности (а не все сопряжены), и существуют нетривиальные отображения ${ displaystyle mathrm {A} _ {3} twoheadrightarrow mathrm {C} _ {3}}$ (на самом деле изоморфизм) и ${ displaystyle mathrm {A} _ {4} twoheadrightarrow mathrm {C} _ {3}.}$

ЧАС₂: Множители Шура

В Множители Шура знакопеременных групп A_п (в случае, когда п не меньше 5) являются циклическими группами порядка 2, за исключением случая, когда п либо 6, либо 7, и в этом случае также имеется тройное покрытие. Следовательно, в этих случаях множитель Шура (циклическая группа) имеет порядок 6.^[2] Впервые они были вычислены в (Щур 1911 ).

${ Displaystyle Н_ {2} ( mathrm {A} _ {n}, mathrm {Z}) = 0}$ для ${ Displaystyle п = 1,2,3}$;

${ Displaystyle Н_ {2} ( mathrm {A} _ {n}, mathrm {Z}) = mathrm {Z} / 2}$ для ${ displaystyle n = 4,5}$;

${ Displaystyle Н_ {2} ( mathrm {A} _ {n}, mathrm {Z}) = mathrm {Z} / 6}$ для ${ displaystyle n = 6,7}$;

${ Displaystyle Н_ {2} ( mathrm {A} _ {n}, mathrm {Z}) = mathrm {Z} / 2}$ для ${ displaystyle n geq 8}$.

Заметки

использованная литература

внешние ссылки

• Вайсштейн, Эрик В. «Переменная группа». MathWorld.
• Вайсштейн, Эрик В. «Переменный групповой граф». MathWorld.