Икосаэдр - Icosahedron
В геометрия, икосаэдр (/ˌаɪkɒsəˈчасяdрən,-kə-,-koʊ-/ или же /аɪˌkɒsəˈчасяdрən/[1]) это многогранник с 20 гранями. Название происходит от Древнегреческий εἴκοσι (eíkosi) означает "двадцать" и от Древнегреческий ἕδρα (Хедра) что означает «место». Множественное число может быть «икосаэдрами» (/-dрə/) или «икосаэдры».
Есть бесконечно много не-похожий формы икосаэдров, некоторые из которых более симметричны, чем другие. Самым известным является (выпуклый, не-звездчатый ) правильный икосаэдр -один из Платоновы тела - чьих лиц 20 равносторонние треугольники.
Правильные икосаэдры
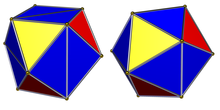
 Выпуклый правильный икосаэдр |  Большой икосаэдр |
Есть два объекта, один выпуклый и один невыпуклый, которые можно назвать правильными икосаэдрами. У каждого 30 ребер и 20 равносторонний треугольник лица с пятью пересечениями в каждой из двенадцати вершин. Как есть икосаэдрическая симметрия. Термин «правильный икосаэдр» обычно относится к выпуклой разновидности, в то время как невыпуклая форма называется большой икосаэдр.
Выпуклый правильный икосаэдр
Выпуклый правильный икосаэдр обычно называют просто правильный икосаэдр, один из пяти регулярных Платоновы тела, и представлен своим Символ Шлефли {3, 5}, содержащий 20 треугольных граней, по 5 граней, пересекающихся вокруг каждой вершины.
Его двойственный многогранник регулярный додекаэдр {5, 3} с тремя правильными пятиугольными гранями вокруг каждой вершины.
Большой икосаэдр
В большой икосаэдр одна из четырех обычных звезд Многогранники Кеплера-Пуансо. Его Символ Шлефли это {3, 5/2}. Как и у выпуклой формы, он также имеет 20 граней равностороннего треугольника, но его вершина представляет собой пентаграмма а не пятиугольник, ведущий к геометрически пересекающимся граням. Пересечения треугольников не представляют новых ребер.
Его двойственный многогранник это большой звездчатый додекаэдр {5/2, 3} с тремя правильными пятиугольными гранями вокруг каждой вершины.
Звездчатые икосаэдры
Звездчатость это процесс расширения граней или ребер многогранника до тех пор, пока они не встретятся, чтобы сформировать новый многогранник. Делается это симметрично, чтобы получившаяся фигура сохранила общую симметрию родительской фигуры.
В их книге Пятьдесят девять икосаэдров, Coxeter et al. перечислил 58 таких звёздчатых звёзд правильного икосаэдра.
Многие из них имеют одну грань в каждой из 20 плоскостей граней и также являются икосаэдрами. Среди них - большой икосаэдр.
Другие звёздчатые звёзды имеют более одной грани в каждой плоскости или образуют соединения более простых многогранников. Это не совсем икосаэдры, хотя их часто называют таковыми.
Пиритоэдрическая симметрия
| Пиритоэдрическая и тетраэдрическая симметрии | |||||
|---|---|---|---|---|---|
| Диаграммы Кокстера |     (пиритоэдрический)  (четырехгранный)  | ||||
| Символ Шлефли | с {3,4} sr {3,3} или | ||||
| Лица | 20 треугольников: 8 равносторонних 12 равнобедренных | ||||
| Края | 30 (6 коротких + 24 длинных) | ||||
| Вершины | 12 | ||||
| Группа симметрии | Тчас, [4,3+], (3 * 2), порядок 24 | ||||
| Группа вращения | Тd, [3,3]+, (332), порядок 12 | ||||
| Двойной многогранник | Пиритоэдр | ||||
| Характеристики | выпуклый | ||||
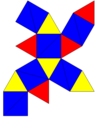
 Сеть | |||||
| |||||
А правильный икосаэдр могут быть искажены или помечены как более низкие пиритоэдрический симметрия[2] и называется курносый октаэдр, курносый тетратетраэдр, курносый тетраэдр, и псевдоикосаэдр. Это можно рассматривать как чередовались усеченный октаэдр. Если все треугольники равносторонний, симметрию также можно отличить, раскрасив по-разному наборы треугольников 8 и 12.
Пиритоэдрическая симметрия имеет символ (3 * 2), [3+, 4], с порядком 24. Тетраэдрическая симметрия имеет символ (332), [3,3]+, с порядком 12. Эти более низкие симметрии допускают геометрические искажения от 20 равносторонних треугольных граней, вместо 8 равносторонних треугольников и 12 конгруэнтных равнобедренные треугольники.
Эти симметрии предлагают Диаграммы Кокстера: и соответственно, каждый из которых представляет низшую симметрию относительно правильный икосаэдр 
, (*532), [5,3] икосаэдрическая симметрия порядка 120.
Декартовы координаты
Координаты 12 вершин могут быть определены векторами, определенными всеми возможными циклическими перестановками и знакопеременами координат формы (2, 1, 0). Эти координаты представляют усеченный октаэдр с чередовались вершины удалены.
Эта конструкция называется курносый тетраэдр в его правильной форме икосаэдра, порожденной теми же операциями, выполняемыми, начиная с вектора (ϕ, 1, 0), где ϕ это Золотое сечение.[2]
Икосаэдр Джессена
В икосаэдре Джессена, иногда называемом Ортогональный икосаэдр Джессена, 12 равнобедренных граней расположены по-разному, так что фигура невыпуклая и имеет верно двугранные углы.
это ножницы конгруэнтные в куб, что означает, что его можно разрезать на более мелкие многогранные части, которые можно переставить, чтобы сформировать твердый куб.
Другие икосаэдры
Ромбический икосаэдр
В ромбический икосаэдр это зоноэдр состоит из 20 одинаковых ромбов. Его можно вывести из ромбический триаконтаэдр удалив 10 средних граней. Несмотря на то, что все грани совпадают, ромбический икосаэдр не лицо переходный.
Симметрии пирамиды и призмы
Общие икосаэдры с пирамидальной и призматической симметрией включают:
- 19-гранный пирамида (плюс 1 основание = 20).
- 18-гранный призма (плюс 2 конца = 20).
- 9-сторонний антипризма (2 подхода по 9 сторон + 2 конца = 20).
- 10-сторонний бипирамида (2 подхода по 10 сторон = 20).
- 10-сторонний трапецоэдр (2 подхода по 10 сторон = 20).
Твердые тела Джонсона
Несколько Твердые тела Джонсона икосаэдры:[3]
| J22 | J35 | J36 | J59 | J60 | J92 |
|---|---|---|---|---|---|
 Гиро-удлиненный треугольный купол |  Ортобикупола удлиненно-треугольной формы |  Гиробикупола удлиненной треугольной формы |  Парабиаугментированный додекаэдр |  Метабиауглеродный додекаэдр |  Гебешфеноротунда треугольная |
 |  |  |  |  |  |
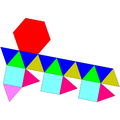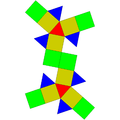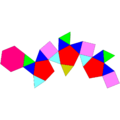| 16 треугольников 3 квадрата 1 шестиугольник | 8 треугольников 12 квадратов | 8 треугольников 12 квадратов | 10 треугольников 10 пятиугольников | 10 треугольников 10 пятиугольников | 13 треугольников 3 квадрата 3 пятиугольника 1 шестиугольник |
Смотрите также
Рекомендации
- ^ Джонс, Дэниел (2003) [1917], Питер Роуч; Джеймс Хартманн; Джейн Сеттер (ред.), Словарь английского произношения, Кембридж: Издательство Кембриджского университета, ISBN 3-12-539683-2
- ^ а б Джон Баэз (11 сентября 2011 г.). "Золото дурака".
- ^ Икосаэдр на Mathworld.
Авторитетный контроль  |
|---|