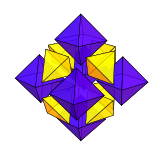
Кубооктаэдр - Cuboctahedron
| Кубооктаэдр | |
|---|---|
 (Нажмите здесь, чтобы повернуть модель) | |
| Тип | Архимедово твердое тело Равномерный многогранник |
| Элементы | F = 14, E = 24, V = 12 (χ = 2) |
| Лица по сторонам | 8{3}+6{4} |
| Обозначение Конвея | AC ааТ |
| Символы Шлефли | г {4,3} или rr {3,3} или |
| т1{4,3} или т0,2{3,3} | |
| Символ Wythoff | 2 | 3 4 3 3 | 2 |
| Диаграмма Кокстера | |
| Группа симметрии | Очас, B3, [4,3], (* 432), порядок 48 Тd, [3,3], (* 332), порядок 24 |
| Группа вращения | О, [4,3]+, (432), заказ 24 |
| Двугранный угол | 125.26° arcsec (-√3) |
| Рекомендации | U07, C19, W11 |
| Характеристики | Полурегулярный выпуклый квазирегулярный |
 Цветные лица |  3.4.3.4 (Фигура вершины ) |
 Ромбический додекаэдр (двойственный многогранник ) |  Сеть |

А кубооктаэдр это многогранник с 8 треугольными гранями и 6 квадратными гранями. В кубооктаэдре 12 одинаковых вершины, с 2 треугольниками и 2 квадратами, пересекающимися в каждом, и 24 идентичными края, каждый из которых отделяет треугольник от квадрата. Таким образом, это квазирегулярный многогранник, т.е. Архимедово твердое тело это не только вершинно-транзитивный но также ребро-транзитивный. Это единственный радиально равносторонний выпуклый многогранник.
Его двойственный многогранник это ромбический додекаэдр.
Кубооктаэдр, вероятно, был известен Платон: Цапля с Определения цитаты Архимед говоря, что Платон знал твердое тело, состоящее из 8 треугольников и 6 квадратов.[1]
Другие имена
- Гептапараллелоэдр (Бакминстер Фуллер )
- Фуллер применил название "Димаксион "к этой форме, которая использовалась в ранней версии Карта Dymaxion. Он также назвал его «векторным равновесием» из-за его радиальной равносторонней симметрии (радиус от центра до вершины равен длине края).[2] Он назвал кубооктаэдр, состоящий из жестких стоек, соединенных гибкими вершинами, «джиттербагом» (эту форму можно постепенно деформировать в икосаэдр, октаэдр, и тетраэдр свернув его квадратные стороны).
- С Oчас симметрии порядка 48, это исправленный куб или же выпрямленный октаэдр (Норман Джонсон )
- С Тd симметрии порядка 24, это скошенный тетраэдр или ромбитетраэтраэдр.
- С D3D симметрии, порядка 12, это треугольный гиробикупола.
Площадь и объем
Площадь А и объем V кубооктаэдра длины ребра а находятся:
Ортогональные проекции
В кубооктаэдр имеет четыре специальных ортогональные проекции, с центром на вершине, ребре и двух типах граней, треугольной и квадратной. Последние два соответствуют букве B2 и А2 Самолеты Кокстера. Косые проекции показывают квадрат и шестиугольник, проходящие через центр кубооктаэдра.
| Квадрат Лицо | Треугольный Лицо | Вершина | Край | Перекос | |
|---|---|---|---|---|---|
 |  |  | |||
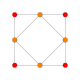 |  | 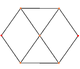 | 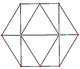 | 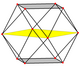 |  |
| [4] | [6] | [2] | [2] | ||
| Ромбический додекаэдр (Двойной многогранник) | |||||
 | 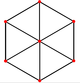 | 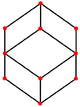 | 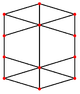 | 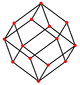 | 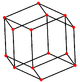 |
Сферическая черепица
Кубооктаэдр также можно представить в виде сферическая черепица, и проецируется на плоскость через стереографическая проекция. Эта проекция конформный, сохраняя углы, но не площади или длины. Прямые линии на сфере проецируются как дуги окружности на плоскость.
 |  |  |  |
| орфографическая проекция | квадрат -центрированный | треугольник -центрированный | Вершина по центру |
|---|---|---|---|
| Стереографическая проекция | |||
Декартовы координаты
В Декартовы координаты для вершин кубооктаэдра (длины ребра √2) с центром в начале координат:
- (±1,±1,0)
- (±1,0,±1)
- (0,±1,±1)
Альтернативный набор координат может быть выполнен в 4-м пространстве, как 12 перестановок:
- (0,1,1,2)
Эта конструкция существует как одна из 16 ортодоксальный грани из скошенный 16-элементный.
Корневые векторы
12 вершин кубооктаэдра могут представлять корневые векторы простая группа Ли А3. При добавлении 6 вершин октаэдр, эти вершины представляют 18 корневых векторов простая группа Ли B3.
Рассечение
В кубооктаэдр можно разделить на два треугольные купола общим шестиугольником, проходящим через центр кубооктаэдра. Если эти два треугольных купола скручены так, что треугольники и квадраты совпадают, Джонсон солид J27, то треугольная ортобикупола, создано.
Кубооктаэдр также можно разрезать на 6 квадратные пирамиды и 8 тетраэдры встреча в центральной точке. Это расслоение выражается в чередующиеся кубические соты где пары квадратных пирамид объединены в октаэдры.
Геометрические отношения

Симметрии

Кубооктаэдр - это уникальный выпуклый многогранник, у которого длинный радиус (от центра до вершины) равен длине ребра; таким образом, его длинный диаметр (от вершины к противоположной вершине) составляет 2 длины ребра. Эта радиальная равносторонняя симметрия является свойством лишь немногих однородных многогранники, в том числе двумерный шестиугольник, трехмерный кубооктаэдр и четырехмерный 24-элементный и 8-элементный (тессеракт). Радиально равносторонний многогранники - это такие многогранники, которые могут быть построены с их длинными радиусами из равносторонних треугольников, которые встречаются в центре многогранника, каждый из которых дает два радиуса и ребро. Следовательно, все внутренние элементы, которые встречаются в центре этих многогранников, имеют равносторонние треугольники, обращенные внутрь, как в разрезе кубооктаэдра на 6 квадратных пирамид и 8 тетраэдров. Каждый из этих радиально равносторонних многогранников также встречается как ячейки характерного заполнения пространства. мозаика: мозаика правильных шестиугольников, ректификованные кубические соты (чередующихся кубооктаэдров и октаэдров), 24-ячеечные соты и тессерактические соты, соответственно. Каждая тесселяция имеет двойная тесселяция; центры ячеек в тесселяции - это вершины ячеек в двойном тесселяции. Самый плотный из известных регулярных сфера-упаковка в двух, трех и четырех измерениях использует центры ячеек одной из этих мозаик как центры сфер.
Кубооктаэдр имеет октаэдрическую симметрию. Его первый звездчатость это сложный из куб и его двойная октаэдр, причем вершины кубооктаэдра расположены в серединах ребер каждого из них.
Конструкции
Кубооктаэдр можно получить, взяв экваториальную поперечное сечение четырехмерного 24-элементный или же 16 ячеек. Шестиугольник можно получить, взяв экваториальное сечение кубооктаэдра.
Кубооктаэдр - это исправленный куб а также исправленный октаэдр.
Это также скошенный тетраэдр. Эта конструкция дает Символ Wythoff: 3 3 | 2. 
При перекосе тетраэдра образуется твердое тело с гранями, параллельными граням кубооктаэдра, а именно восемь треугольников двух размеров и шесть прямоугольников. Пока его края не равны, это твердое тело остается вершинно-однородный: твердое тело имеет полный тетраэдр группа симметрии и его вершины эквивалентны в этой группе.
Ребра кубооктаэдра образуют четыре правильных шестиугольники. Если кубооктаэдр разрезать в плоскости одного из этих шестиугольников, каждая половина будет треугольный купол, один из Твердые тела Джонсона; поэтому сам кубооктаэдр также можно назвать треугольным гиробикупола, самая простая из серии (кроме гиробифастигий или «дигональные гиробикуполы»). Если половинки соединить вместе с поворотом так, чтобы треугольники встретились с треугольниками, а квадраты встретились с квадратами, в результате получится еще одно твердое тело Джонсона, треугольная ортобикупола, также называемый антикубооктаэдром.
Обе треугольные двуполости важны для упаковка сфер. Расстояние от центра твердого тела до его вершин равно длине его ребра. Каждый центральный сфера может иметь до двенадцати соседей, и в гранецентрированной кубической решетке они занимают позиции вершин кубооктаэдра. В шестиугольник В плотноупакованной решетке они соответствуют углам треугольного ортобикупола. В обоих случаях центральная сфера занимает положение центра твердого тела.
Кубооктаэдры появляются в виде ячеек в трех выпуклые однородные соты а в девяти выпуклых равномерные 4-многогранники.
Объем кубооктаэдра равен 5/6 окружающего куба и 5/8 окружающего октаэдра.
Расположение вершин
Поскольку он радиально равносторонний, центр кубооктаэдра можно рассматривать как 13-ю. каноническая апикальная вершина, на одно ребро, удаленное от 12 обычных вершин, так как вершина из каноническая пирамида длина одного ребра, равноудаленного от остальных его вершин.
Кубооктаэдр имеет общие ребра и расположение вершин с двумя невыпуклые равномерные многогранники: the кубогемиоктаэдр (имеющий общие квадратные грани) и октагемиоктаэдр (имеющий общие треугольные грани). Он также служит канеллированным тетраэдр, как исправленный тетратраэдр.
 Кубооктаэдр |  Кубогемиоктаэдр |  Октагемиоктаэдр |
Кубооктаэдр 2-обложки то тетрагемигексаэдр,[3] который соответственно имеет такой же Абстрактные вершина фигуры (два треугольника и два квадрата: 3.4.3.4) и половину вершин, ребер и граней. (Фактическая фигура вершины тетрагемигексаэдра равна 3,4.3/2.4, с а/2 фактор из-за креста.)
 Кубооктаэдр |  Тетрагемигексаэдр |
Связанные многогранники
Кубооктаэдр - один из семейства однородных многогранников, связанных с кубом и правильным октаэдром.
| Однородные октаэдрические многогранники | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Симметрия: [4,3], (*432) | [4,3]+ (432) | [1+,4,3] = [3,3] (*332) | [3+,4] (3*2) | |||||||
| {4,3} | т {4,3} | г {4,3} г {31,1} | т {3,4} т {31,1} | {3,4} {31,1} | рр {4,3} s2{3,4} | tr {4,3} | sr {4,3} | ч {4,3} {3,3} | час2{4,3} т {3,3} | с {3,4} с {31,1} |
= | = | = | ||||||||
| Двойники к однородным многогранникам | ||||||||||
| V43 | V3.82 | V (3,4)2 | V4.62 | V34 | V3.43 | V4.6.8 | V34.4 | V33 | V3.62 | V35 |
Кубооктаэдр также имеет тетраэдрическую симметрию с двумя цветами треугольников.
| Семейство равномерных тетраэдрических многогранников | |||||||
|---|---|---|---|---|---|---|---|
| Симметрия: [3,3], (*332) | [3,3]+, (332) | ||||||
 |  |  |  | ||||
| {3,3} | т {3,3} | г {3,3} | т {3,3} | {3,3} | рр {3,3} | tr {3,3} | ср {3,3} |
| Двойники к однородным многогранникам | |||||||
 |  |  |  | ||||
| V3.3.3 | V3.6.6 | V3.3.3.3 | V3.6.6 | V3.3.3 | V3.4.3.4 | V4.6.6 | V3.3.3.3.3 |
Связанные квазирегулярные многогранники и мозаики
Кубооктаэдр существует в последовательности симметрий квазирегулярных многогранников и мозаик с конфигурации вершин (3.п)2, переходя от мозаики сферы к евклидовой плоскости и к гиперболической плоскости. С орбифолдная запись симметрия *п32 все эти мозаики Wythoff Construction в пределах фундаментальная область симметрии, с образующими точками в правом углу области.[4][5]
| *п32 орбифолдные симметрии квазирегулярных мозаик: (3.п)2 | |||||||
|---|---|---|---|---|---|---|---|
Строительство | Сферический | Евклидово | Гиперболический | ||||
| *332 | *432 | *532 | *632 | *732 | *832... | *∞32 | |
| Квазирегулярный цифры |  |  |  |  |  |  |  |
| Вершина | (3.3)2 | (3.4)2 | (3.5)2 | (3.6)2 | (3.7)2 | (3.8)2 | (3.∞)2 |
| *п42 изменения симметрии квазирегулярных мозаик: (4.п)2 | ||||||||
|---|---|---|---|---|---|---|---|---|
| Симметрия *4п2 [n, 4] | Сферический | Евклидово | Компактный гиперболический | Паракомпакт | Некомпактный | |||
| *342 [3,4] | *442 [4,4] | *542 [5,4] | *642 [6,4] | *742 [7,4] | *842 [8,4]... | *∞42 [∞,4] | [пя, 4] | |
| Цифры |  |  |  |  |  |  |  | |
| Конфиг. | (4.3)2 | (4.4)2 | (4.5)2 | (4.6)2 | (4.7)2 | (4.8)2 | (4.∞)2 | (4.пя)2 |
Этот многогранник топологически связан как часть последовательности скошенный многогранники с вершиной фигуры (3.4.п.4) и продолжается как мозаика гиперболическая плоскость. Эти вершинно-транзитивный цифры имеют (*п32) Reflectional (отражающий) симметрия.
| *п32 мутации симметрии расширенных мозаик: 3.4.п.4 | ||||||||
|---|---|---|---|---|---|---|---|---|
| Симметрия *п32 [n, 3] | Сферический | Евклид. | Компактная гиперболия. | Paracomp. | ||||
| *232 [2,3] | *332 [3,3] | *432 [4,3] | *532 [5,3] | *632 [6,3] | *732 [7,3] | *832 [8,3]... | *∞32 [∞,3] | |
| Фигура |  |  |  |  |  |  |  | |
| Конфиг. | 3.4.2.4 | 3.4.3.4 | 3.4.4.4 | 3.4.5.4 | 3.4.6.4 | 3.4.7.4 | 3.4.8.4 | 3.4.∞.4 |
Связанные многогранники

Кубооктаэдр можно разложить на правильный октаэдр и восемь неправильных, но равных октаэдров в форме выпуклой оболочки куба с удаленными двумя противоположными вершинами. Это разложение кубооктаэдра соответствует параллельной проекции плоскости на первую ячейку. 24-элементный в трех измерениях. Под этой проекцией кубооктаэдр образует оболочку проекции, которую можно разложить на шесть квадратных граней, правильный октаэдр и восемь неправильных октаэдров. Эти элементы соответствуют изображениям шести октаэдрических ячеек в 24-ячейке, ближайшей и самой дальней ячеек с точки зрения 4D и оставшимся восьми парам ячеек, соответственно.
Культурные события

- в Звездный путь эпизод "Любым другим именем "инопланетяне захватывают Предприятие превращая членов экипажа в неодушевленные кубооктаэдры.
- Игрушка-непоседа "Geo Twister" [1] - изгибаемый кубооктаэдр.
- Космические станции Кориолиса в серии компьютерных игр Элитный имеют форму кубооктаэдра.
- Весак Кууду, традиционные фонари, которые делают в Шри-Ланке ежегодно в честь дня Весак Пойя, обычно имеют кубооктаэдрическую форму.
- "Лунные змеи" из Супер Марио Одиссея.[6]
- InfluxData, компания, стоящая за InfluxDB база данных временных рядов, использует кубооктаэдр в его логотипе.
Кубооктаэдрический граф
| Кубооктаэдрический граф | |
|---|---|
 4-х кратная симметрия | |
| Вершины | 12 |
| Края | 24 |
| Автоморфизмы | 48 |
| Характеристики | |
| Таблица графиков и параметров | |
в математический поле теория графов, а кубооктаэдрический граф это граф вершин и ребер кубооктаэдра, один из Архимедовы тела. Его также можно построить как линейный график куба. Имеет 12 вершины и 24 ребра, это локально линейный, и является квартика Архимедов граф.[7]
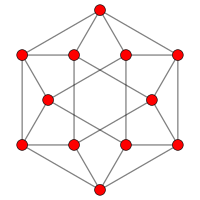 6-кратная симметрия |
Смотрите также
Рекомендации
- ^ Хит, Томас Л. (1931), Учебник греческой математики, Кларендон, стр. 176
- ^ Векторное равновесие: Р. Бакминстер Фуллер
- ^ Рихтер, Дэвид А., Две модели реальной проективной плоскости, заархивировано из оригинал на 2016-03-03, получено 2010-04-15
- ^ Кокстер, Х. С. М. (1973), Правильные многогранники (3-е изд.), Дувр, Глава V: Калейдоскоп, Раздел: 5.7 Построение Витхоффа, ISBN 0-486-61480-8
- ^ Двумерные мутации симметрии Дэниел Хьюсон
- ^ "Файл: Moonsnake Icon SMO.png - Super Mario Wiki, энциклопедия Марио". www.mariowiki.com. Получено 2018-11-05.
- ^ Читать, R.C .; Уилсон, Р. Дж. (1998), Атлас графиков, Oxford University Press, п. 269
дальнейшее чтение
- Гика, Матила (1977). Геометрия искусства и жизни ([Nachdr.] Ред.). Нью-Йорк: Dover Publications. стр.51–56, 81–84. ISBN 9780486235424.
- Вайсштейн, Эрик В. (2002). «Кубооктаэдр». CRC Краткая энциклопедия математики (2-е изд.). Хобокен: CRC Press. С. 620–621. ISBN 9781420035223.
- Уильямс, Роберт (1979). Геометрическая основа естественной структуры: первоисточник дизайна. Dover Publications, Inc. ISBN 0-486-23729-X. (Раздел 3-9)
- Кромвель, П. Многогранники, CUP hbk (1997), pbk. (1999). Глава 2 с. 79–86 Архимедовы тела
внешняя ссылка
- Равномерные многогранники
- Многогранники виртуальной реальности Энциклопедия многогранников
- Эрик В. Вайсштейн, Кубооктаэдр (Архимедово твердое тело ) в MathWorld.
- Кубооктаэдр на Hexnet сайт, посвященный математике шестиугольника.
- Клитцинг, Ричард. "3D выпуклые равномерные многогранники o3x4o - co".
- Редактируемая печатная сетка кубооктаэдра с интерактивным трехмерным изображением