Призма (геометрия) - Prism (geometry)

Набор равномерных призм
(Показана шестиугольная призма)
Тип	равномерный многогранник
Обозначения многогранника Конвея	пп
Лица	2+п общий: 2 {n} п {4}
Края	3п
Вершины	2п
Символ Шлефли	{n} × {}^[1] или же т{2, п}
Диаграмма Кокстера
Конфигурация вершины	4.4.п
Группа симметрии	D_пчас, [п,2], (*п22), порядок 4п
Группа вращения	D_п, [п,2]⁺, (п22), порядок 2п
Двойной многогранник	п-гональный бипирамида
Характеристики	выпуклый, полурегулярный, вершинно-транзитивный
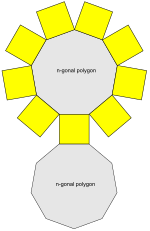п-угольная призматическая сетка (п = 9 здесь)

В геометрия, а призма это многогранник включая п-сторонний многоугольный основание, вторая база, которая является переведено копия (жестко перемещенная без вращения) первой, и п Другой лица (обязательно все параллелограммы ) присоединение соответствующие стороны из двух баз. Все поперечные сечения параллельно базам идут переводы баз. Призмы названы в честь их оснований; пример: призма с пятиугольник основание называется пятиугольной призмой. Призмы являются подклассом призматоиды.

Как и многие основные геометрические термины, слово призма (Греческий: πρίσμα, романизированный: призма, горит 'что-то распиленное') впервые было использовано в Элементы Евклида. Евклид определил термин в книге XI как «твердую фигуру, содержащуюся в двух противоположных, равных и параллельных плоскостях, а остальные - параллелограммы». Однако это определение подвергалось критике за то, что оно недостаточно конкретное по отношению к природе оснований, что вызвало путаницу среди более поздних геометрических авторов.^[2]^[3]

Общие, правильные и однородные призмы

А правая призма представляет собой призму, в которой стыкующиеся кромки и грани перпендикуляр к базовым граням.^[4] Это применимо, если соединяющиеся грани прямоугольный. Если соединяемые кромки и грани не перпендикулярны базовым граням, это называется наклонная призма.

Например параллелепипед является наклонная призма из которых база является параллелограмм, или, что то же самое, многогранник с шестью гранями, которые являются параллелограммами.

Усеченная треугольная призма с усеченной под косым углом верхней гранью.

А усеченная призма - призма с непараллельными верхней и нижней гранями.^[5]

В некоторых текстах может применяться термин прямоугольная призма или же квадратная призма как для правой прямоугольной призмы, так и для правой квадратной призмы. А правая p-угольная призма с прямоугольными сторонами имеет символ Шлефли {} × {p}.

Правую прямоугольную призму еще называют кубовид, или неофициально прямоугольная коробка. Правая квадратная призма - это просто квадратная коробка, а также может называться квадратный кубоид. А правая прямоугольная призма имеет Символ Шлефли { }×{ }×{ }.

An п-призма, имеющая правильный многоугольник заканчивается и прямоугольный стороны, подходит к цилиндрический твердый как п подходы бесконечность.

Период, термин однородная призма или же полуправильная призма может использоваться для правая призма с квадрат сторон, так как такие призмы входят в набор равномерные многогранники. А однородная p-угольная призма имеет Символ Шлефли т {2, р}. Правые призмы с правильным основанием и равной длиной ребер образуют одну из двух бесконечных серий полуправильные многогранники, другая серия антипризмы.

В двойной из правая призма это бипирамида.

Объем

В объем призмы - это продукт площадь основания и расстояния между двумя гранями основания или высоты (в случае неправильной призмы, обратите внимание, что это означает перпендикулярное расстояние).

Таким образом, объем составляет:

{ Displaystyle V = Bh}

куда B это базовая площадь и час это высота. Объем призмы, основанием которой является п-сторонний правильный многоугольник с длиной стороны s следовательно является:

{ displaystyle V = { frac {n} {4}} hs ^ {2} cot left ({ frac { pi} {n}} right)}

Площадь поверхности

Поверхность площадь правой призмы:

{ displaystyle 2B + Ph}

куда B площадь основания, час высота, и п база периметр.

Площадь поверхности правой призмы с правильным основанием п-сторонний многоугольник с длиной стороны s и высота час следовательно является:

{ displaystyle A = { frac {n} {2}} s ^ {2} cot { left ({ frac { pi} {n}} right)} + nsh}

Диаграммы Шлегеля

P3	P4	P5	P6	P7	P8

Симметрия

В группа симметрии права п-сторонняя призма с регулярным основанием D_пчас порядка 4п, за исключением куба, имеющего большую группу симметрии О_час порядка 48, который имеет три версии D_4ч в качестве подгруппы. В группа ротации это D_п порядка 2п, за исключением случая куба, который имеет большую группу симметрии O порядка 24, который имеет три версии D₄ как подгруппы.

Группа симметрии D_пчас содержит инверсия если только п даже.

В Hosohedra и дигедра также обладают двугранной симметрией, и n-угольную призму можно построить с помощью геометрическое усечение n-угольного хозоэдра, а также через песня или же расширение n-угольного диэдра.

Призматический многогранник

А призматический многогранник является многомерным обобщением призмы. An п-мерный призматический многогранник строится из двух (п − 1) -мерные многогранники, переведенные в следующее измерение.

Призматический п-элементы многогранника дублируются из (п − 1) -элементы многогранника, а затем создание новых элементов из следующего нижнего элемента.

Принять п-политоп с ж_я я-лицо элементы (я = 0, ..., п). Его (п + 1) -полигонная призма будет иметь 2ж_я + ж_я−1 я-лицевые элементы. (С ж₋₁ = 0, ж_п = 1.)

По размеру:

Взять многоугольник с п вершины, п края. Его призма имеет 2п вершины, 3п края и 2 + п лица.
Взять многогранник с v вершины, е края и ж лица. Его призма имеет 2v вершины, 2е + v края, 2ж + е лица, и 2 + ж клетки.
Взять полихорон с v вершины, е края, ж лица и c клетки. Его призма имеет 2v вершины, 2е + v края, 2ж + е лица, и 2c + ж клетки и 2 + c гиперячейки.

Однородный призматический многогранник

Обычный п-полигон, представленный Символ Шлефли {п, q, ..., т} может образовывать однородную призматическую (п + 1) -многогранник, представленный Декартово произведение из два символа Шлефли: {п, q, ..., т}×{}.

По размеру:

0-политопная призма - это отрезок, представленный пустым Символ Шлефли {}.
1-многогранная призма - это прямоугольник, состоящий из 2-х переведенных отрезков. Он представлен в виде символа произведения Шлефли {} × {}. Если это квадрат, симметрия может быть понижена: {}×{} = {4}.
- Пример: квадрат, {} × {}, два параллельных отрезка, соединенные двумя отрезками. стороны.
А многоугольный призма - это трехмерная призма, состоящая из двух сдвинутых многоугольников, соединенных прямоугольниками. Правильный многоугольник {п} может построить униформу п-угольная призма, представленная продуктом {п} × {}. Если п = 4, при симметрии сторон квадрата он становится куб: {4}×{} = {4, 3}.
- Пример: Пятиугольная призма, {5} × {}, два параллельных пятиугольники соединены 5 прямоугольными стороны.
А многогранник призма - это четырехмерная призма, состоящая из двух сдвинутых многогранников, соединенных трехмерными призменными ячейками. Правильный многогранник {п, q} можно построить однородную полихорическую призму, представленную произведением {п, q} × {}. Если многогранник представляет собой куб, а стороны - кубы, он становится тессеракт: {4, 3}×{} = {4, 3, 3}.
- Пример: Додекаэдрическая призма, {5, 3} × {}, два параллельных додекаэдр соединены 12 пятиугольной призмой стороны.
...

Призматические многогранники более высокого порядка также существуют как декартовы продукты любых двух многогранников. Размерность многогранника - произведение размеров элементов. Первый пример их существования в 4-мерном пространстве называется дуопризма как произведение двух многоугольников. Регулярные дуопризмы представлены как {п}×{q}.

Семья униформы призмы [ v т е ]
Многогранник
Coxeter
Плитка
Конфиг.	2.4.4	3.4.4	4.4.4	5.4.4	6.4.4	7.4.4	8.4.4	9.4.4	10.4.4	11.4.4	12.4.4

Витая призма

А витая призма - невыпуклый призматический многогранник, построенный равномерным q-призмы с боковыми гранями, разделенными пополам по квадратной диагонали и закрученной наверху, обычно на $π$ /q радианы (180/q градусов) в том же направлении, в результате чего боковые треугольники будут вогнутыми.^[6]^[7]

Закрученной призмы не может быть рассеченный в тетраэдры без добавления новых вершин. Наименьший корпус треугольной формы называется Многогранник Шёнхардта.

А витая призма топологически идентичен антипризма, но имеет половину симметрия: D_п, [п,2]⁺, порядок 2п. Его можно рассматривать как выпуклую антипризму с удаленными тетраэдрами между парами треугольников.

3-угольный	4-угольный		12-угольный
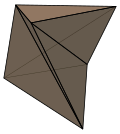Многогранник Шёнхардта	Скрученная квадратная призма	Квадратная антипризма	Скрученная двенадцатигранная антипризма

Frustum

Пятиугольный усеченный

А усеченный топологически идентичен призме, с трапеция боковые грани и верхние и нижние многоугольники разного размера.

Звездная призма

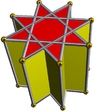
А звездная призма - невыпуклый многогранник, состоящий из двух одинаковых звездный многоугольник грани сверху и снизу, параллельны, смещены на расстояние и соединены прямоугольными гранями. А однородная звездная призма буду иметь Символ Шлефли {п/q} × {}, с п прямоугольник и 2 {п/q} лиц. Он топологически идентичен п-угольная призма.

Примеры
{ }×{ }₁₈₀×{ }	т_а {3}×{ }		{5/2}×{ }	{7/2}×{ }	{7/3}×{ }	{8/3}×{ }
D_2ч, заказ 8	D_3ч, заказ 12		D_5ч, заказ 20	D_7ч, заказ 28		D_8ч, заказ 32

Перекрещенная призма

А пересеченная призма - невыпуклый многогранник, построенный из призмы, у которого базовые вершины перевернутый вокруг центра (или повернутый на 180 °). Это преобразует боковые прямоугольные грани в скрещенные прямоугольники. Для правильной многоугольной основы внешний вид п-гональный песочные часы, со всеми вертикальными ребрами, проходящими через единый центр, но без вершины. Он топологически идентичен п-угольная призма.

Примеры
{ }×{ }₁₈₀×{ }₁₈₀	т_а{3}×{ }₁₈₀		{3}×{ }₁₈₀	{4}×{ }₁₈₀	{5}×{ }₁₈₀	{5/2}×{ }₁₈₀	{6}×{ }₁₈₀
D_2ч, заказ 8	D_3D, заказ 12			D_4ч, заказ 16	D_5d, заказ 20		D_6d, заказ 24

Тороидальные призмы

А тороидальная призма невыпуклый многогранник подобен пересеченная призма за исключением того, что вместо базового и верхнего многоугольников добавляются простые прямоугольные боковые грани, замыкающие многогранник. Это можно сделать только для одноугольных базовых полигонов. Это топологические торы с Эйлерова характеристика нуля. Топологический многогранная сетка можно вырезать из двух рядов квадратная черепица, с вершина фигура 4.4.4.4. А п-угольная тороидальная призма имеет 2п вершины и грани, и 4п края и топологически самодвойственный.

Примеры
D_4ч, заказ 16	D_6ч, заказ 24
v = 8, e = 16, f = 8	v = 12, e = 24, f = 12

Смотрите также

внешняя ссылка

Вайсштейн, Эрик В. "Призма". MathWorld.
Бумажные модели призм и антипризм Свободные сети призм и антипризм
Бумажные модели призм и антипризм Использование сетей, созданных Стелла

[1] N.W. Джонсон: Геометрии и преобразования, (2018) ISBN 978-1-107-10340-5 Глава 11: Конечные группы симметрии, 11.3 Пирамиды, призмы и антипризмы, рисунок 11.3b

[Malton1774-2] Томас Мальтон (1774 г.). Королевский путь к геометрии: или простое и знакомое введение в математику. ... Томасом Малтоном. ... автор, так и продал. С. 360–.

[Elliot1845-3] Джеймс Эллиот (1845). Ключ к полному трактату по практической геометрии и измерениям: содержащему полные демонстрации правил ... Лонгман, Браун, Грин и Лонгманс. С. 3–.

[4] Уильям Ф. Керн, Джеймс Р. Бланд,Твердое измерение с доказательствами, 1938, с.28

[5] Уильям Ф. Керн, Джеймс Р. Бланд,Твердое измерение с доказательствами, 1938, с.81

[6] Факты в досье: Справочник по геометрии, Екатерина А. Горини, 2003 г., ISBN 0-8160-4875-4, стр.172

[7] [1]

[1]

[2]

[3]

[4]

[5]

[6]

[7]