Выпрямленная призма - Википедия - Rectified prism

Набор ректифицированных призм
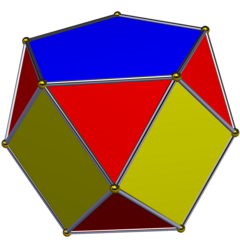Выпрямленная пятиугольная призма
Обозначения многогранника Конвея	APп
Лица	2 п-угольники п квадраты 2п треугольники
Края	6п
Вершины	3п
Группа симметрии	Dпчас, [2,2п], (*22п), порядок 4п
Группа вращения	Dп, [2,п]+, (22п), порядок 2п
Двойной многогранник	Присоединенная призма
Характеристики	выпуклый

В геометрия, а выпрямленная призма (также выпрямленная бипирамида) является одним из бесконечного множества многогранники, построенный как исправление из п-гональный призма, усекая вершины до середины исходных ребер. В Обозначения многогранника Конвея, он представлен как APN, амвоническая призма. Боковые квадраты или прямоугольные грани призмы становятся квадратами или ромбическими гранями, а новые равнобедренный треугольник грани - это усечения исходных вершин.

Элементы

An п-гональная форма имеет 3п вершины, 6п ребра и 2 + 3п лица: 2 обычных п-угольники, п ромбовидные и 2п треугольники.

Формы

В выпрямленная квадратная призма то же самое, что и полуправильный кубооктаэдр.

п	3	4	5	6	8	п
Изображение
Сеть
Связанный		Кубооктаэдр

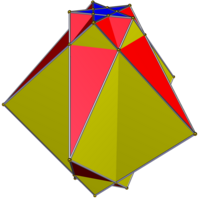
Выпрямленные звездные призмы также существуют, например, формы 5/2:

Двойной

Набор стыкованных призм
Соединенная пятиугольная призма
Обозначения многогранника Конвея	jPп
Лица	3п
Края	6п
Вершины	2+3п
Группа симметрии	Dпчас, [2,2п], (*22п), порядок 4п
Группа вращения	Dп, [2,п]+, (22п), порядок 2п
Двойной многогранник	Выпрямленная призма Ректифицированная бипирамида
Характеристики	выпуклый

Двойник выпрямленная призма это присоединенная призма или же присоединился к бипирамиде, в Обозначения многогранника Конвея. Операция соединения добавляет вершины в центре граней и заменяет ребра ромбическими гранями между исходным и соседним центрами граней. В соединенная квадратная призма та же топология, что и ромбический додекаэдр. В соединенная треугольная призма это Граф Гершеля.

п	3	4	5	6	8	п
Изображение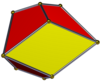
Сеть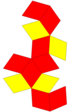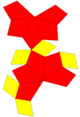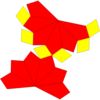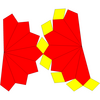
Связанный		Ромбический додекаэдр

Смотрите также

• Ректифицированная антипризма

внешняя ссылка

• Обозначение Конвея для многогранников Попробуйте: APп и jPп, куда п= 3,4,5,6 ... пример aP4 - это выпрямленная квадратная призма, а jP4 - соединенная квадратная призма.

Этот многогранник -связанная статья является заглушка. Вы можете помочь Википедии расширяя это.