Усеченный куб - Truncated cube

Усеченный кубический граф
	4-х кратная симметрия Диаграмма Шлегеля
Вершины	24
Края	36
Автоморфизмы	48
Хроматическое число	3
Характеристики	Кубический, Гамильтониан, обычный, нулевой симметричный
	Таблица графиков и параметров

Усеченный куб
(Нажмите здесь, чтобы повернуть модель)
Тип	Архимедово твердое тело Равномерный многогранник
Элементы	F = 14, E = 36, V = 24 (χ = 2)
Лица по сторонам	8{3}+6{8}
Обозначение Конвея	tC
Символы Шлефли	т {4,3}
Символы Шлефли	т_0,1{4,3}
Символ Wythoff	2 3 \| 4
Диаграмма Кокстера
Группа симметрии	О_час, B₃, [4,3], (* 432), порядок 48
Группа вращения	О, [4,3]⁺, (432), заказ 24
Двугранный угол	3-8: 125°15′51″ 8-8: 90°
Рекомендации	U₀₉, C₂₁, W₈
Характеристики	Полурегулярный выпуклый
Цветные лица	3.8.8 (Фигура вершины )
Октаэдр Триаки (двойственный многогранник )	Сеть

3D модель усеченного куба

В геометрия, то усеченный куб, или же усеченный шестигранник, является Архимедово твердое тело. Имеет 14 правильных граней (6 восьмиугольный и 8 треугольный ), 36 ребер и 24 вершины.

Если усеченный куб имеет единичную длину ребра, его двойная триакис октаэдр имеет ребра длиной 2 и 2+√2.

Площадь и объем

Площадь А и объем V усеченного куба с длиной ребра а находятся:

{ displaystyle { begin {align} A & = 2 left (6 + 6 { sqrt {2}} + { sqrt {3}} right) a ^ {2} && приблизительно 32.434 , 6644a ^ { 2} V & = { frac {21 + 14 { sqrt {2}}} {3}} a ^ {3} && приблизительно 13.599 , 6633a ^ {3}. End {align}}}

Ортогональные проекции

В усеченный куб имеет пять специальных ортогональные проекции по центру на вершине, на двух типах ребер и двух типах граней: треугольниках и восьмиугольниках. Последние два соответствуют букве B₂ и А₂ Самолеты Кокстера.

Ортогональные проекции
В центре	Вершина	Край 3-8	Край 8-8	Лицо Восьмиугольник	Лицо Треугольник
Твердый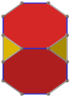
Каркас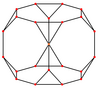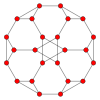
Двойной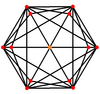
Проективный симметрия	[2]	[2]	[2]	[4]	[6]

Сферическая черепица

Усеченный куб также можно представить в виде сферическая черепица, и проецируется на плоскость через стереографическая проекция. Эта проекция конформный, сохраняя углы, но не площади или длины. Прямые на сфере проецируются как дуги окружности на плоскость.

Ортографическая проекция	Стереографические проекции
	восьмиугольник -центрированный	треугольник -центрированный

Декартовы координаты

Усеченный куб с восьмиугольными гранями пиритоэдрически рассечена с центральной вершиной на треугольники и пятиугольники, создавая топологические икосододекаэдр

Декартовы координаты для вершин усеченный шестигранник с центром в начале координат с длиной ребра 2ξ все перестановки

(±ξ, ±1, ±1),

куда ξ = √2 − 1.

Параметр ξ может варьироваться в пределах ± 1. Значение 1 дает куб, 0 производит кубооктаэдр, а отрицательные значения создают самопересекающиеся октаграмматический лица.

Если самопересекающиеся части октаграмм удаляются, оставляя квадраты и усекая треугольники на шестиугольники, усеченные октаэдры производятся, и последовательность заканчивается уменьшением центральных квадратов до точки и созданием октаэдр.

Рассечение

Рассеченный усеченный куб с разложенными элементами

Усеченный куб можно разрезать на центральную куб, с шестью квадратный купол вокруг каждой из граней куба и 8 правильных четырехгранников по углам. Это рассечение также можно увидеть в рунические кубические соты, с куб, тетраэдр, и ромбокубооктаэдр клетки.

Это рассечение можно использовать для создания Тороид Стюарта со всеми правильными гранями, удалив два квадратных купола и центральный куб. Этот выкопанный куб имеет 16 треугольники, 12 квадраты, и 4 восьмиугольники.^[1]^[2]

Расположение вершин

Он разделяет расположение вершин с тремя невыпуклые равномерные многогранники:

Усеченный куб	Невыпуклый большой ромбокубооктаэдр	Большой кубокубооктаэдр	Большой ромбогексаэдр

Связанные многогранники

Усеченный куб симметрично связан с другими многогранниками и мозаиками.

Усеченный куб - один из семейства однородных многогранников, связанных с кубом и правильным октаэдром.

Однородные октаэдрические многогранники
Симметрия: [4,3], (*432)							[4,3]⁺ (432)	[1⁺,4,3] = [3,3] (*332)		[3⁺,4] (3*2)
{4,3}	т {4,3}	г {4,3} г {3^1,1}	т {3,4} т {3^1,1}	{3,4} {3^1,1}	рр {4,3} s₂{3,4}	tr {4,3}	sr {4,3}	ч {4,3} {3,3}	час₂{4,3} т {3,3}	с {3,4} с {3^1,1}

		=	=	=				= или же	= или же	=

Двойники к однородным многогранникам
V4³	V3.8²	V (3,4)²	V4.6²	V3⁴	V3.4³	V4.6.8	V3⁴.4	V3³	V3.6²	V3⁵

Мутации симметрии

Этот многогранник топологически связан как часть последовательности равномерных усеченный многогранники с конфигурации вершин (3.2п.2п), и [п,3] Группа Коксетера симметрия, а также серия многогранников и мозаик п.8.8.

*п32 мутация симметрии усеченных сферических мозаик: t {п,3}
Симметрия *п32 [n, 3]	Сферический				Евклид.	Компактная гиперболия.		Paraco.
Симметрия *п32 [n, 3]	*232 [2,3]	*332 [3,3]	*432 [4,3]	*532 [5,3]	*632 [6,3]	*732 [7,3]	*832 [8,3]...	*∞32 [∞,3]
Усеченный цифры
Символ	т {2,3}	т {3,3}	т {4,3}	т {5,3}	т {6,3}	т {7,3}	т {8,3}	т {∞, 3}
Triakis цифры
Конфиг.	V3.4.4	V3.6.6	V3.8.8	V3.10.10	V3.12.12	V3.14.14	V3.16.16	V3.∞.∞

*п42 мутации симметрии усеченных мозаик: п.8.8 [ v т е ]
Симметрия *п42 [n, 4]	Сферический		Евклидово	Компактный гиперболический				Паракомпакт
Симметрия *п42 [n, 4]	*242 [2,4]	*342 [3,4]	*442 [4,4]	*542 [5,4]	*642 [6,4]	*742 [7,4]	*842 [8,4]...	*∞42 [∞,4]
Усеченный цифры
Конфиг.	2.8.8	3.8.8	4.8.8	5.8.8	6.8.8	7.8.8	8.8.8	∞.8.8
н-кис цифры
Конфиг.	V2.8.8	V3.8.8	V4.8.8	V5.8.8	V6.8.8	V7.8.8	V8.8.8	V∞.8.8

Альтернативное усечение

Тетраэдр, его обрезание по краю и усеченный куб

Усечение чередующихся вершин куба дает тетраэдр с фаской, т.е. обрезание ребра тетраэдра.

В усеченный треугольный трапецоэдр - это еще один многогранник, который может быть образован путем обрезания ребра куба.

Связанные многогранники

В усеченный куб, является вторым в последовательности усеченных гиперкубы:

Усеченные гиперкубы
Изображение								...
Имя	Восьмиугольник	Усеченный куб	Усеченный тессеракт	Усеченный 5-куб	Усеченный 6-куб	Усеченный 7-куб	Усеченный 8-куб
Диаграмма Кокстера
Фигура вершины	() v ()	() v {}	() v {3}	() v {3,3}	() v {3,3,3}	() v {3,3,3,3}	() v {3,3,3,3,3}