Усечение (геометрия) - Truncation (geometry)

Усеченный квадрат - это правильный восьмиугольник: t {4} = {8} 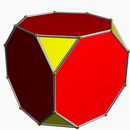=	Усеченный куб т {4,3} или	Усеченные кубические соты т {4,3,4} или

В геометрия, а усечение это операция в любом измерении, которая сокращает многогранник вершины, создавая новый грань вместо каждой вершины. Термин происходит от Кеплер имена для Архимедовы тела.

Равномерное усечение

В общем любые многогранник (или многогранник) также может быть усечен со степенью свободы относительно глубины разреза, как показано на Обозначения многогранника Конвея операция усечения.

Обычно подразумевается особый вид усечения: равномерное усечение, оператор усечения, применяемый к правильный многогранник (или же правильный многогранник ), что создает результирующий равномерный многогранник (равномерный многогранник ) с равной длиной ребра. Нет степеней свободы, и он представляет собой фиксированную геометрическую форму, как и правильные многогранники.

В общем, все однокольцевые однородные многогранники имеют равномерное усечение. Например, икосододекаэдр, представленный как Символы Шлефли г {5,3} или ${displaystyle {egin {Bmatrix} 5 3end {Bmatrix}}}$ , и Диаграмма Кокстера-Дынкина или же имеет равномерное усечение, усеченный икосододекаэдр, представленный как tr {5,3} или ${displaystyle t {egin {Bmatrix} 5 3end {Bmatrix}}}$ , . в Диаграмма Кокстера-Дынкина, эффект усечения заключается в вызове всех узлов, смежных с кольцевым узлом.

Равномерное усечение выполняется на регулярной треугольная черепица {3,6} результатов в обычном шестиугольная черепица {6,3}.

Усечение полигонов

Усеченный n-сторонний многоугольник будет иметь 2n сторон (ребер). Правильный многоугольник, равномерно усеченный, станет другим правильным многоугольником: t {n} равно {2n}. Полное усечение (или исправление ), r {3}, - еще один правильный многоугольник в своем двойной позиция.

Правильный многоугольник также можно представить Диаграмма Кокстера-Дынкина, , и его равномерное усечение , и его полное усечение . График представляет Группа Коксетера я₂(n), где каждый узел представляет зеркало, а край представляет угол π /п между зеркалами, а вокруг одного или обоих зеркал дан кружок, чтобы показать, какие из них активны.

Параметрические усечения треугольника
{3}		t {3} = {6}		г {3} = {3}

Звездные многоугольники также может быть усечено. Усеченный пентаграмма {5/2} будет выглядеть как пятиугольник, но на самом деле это двойное покрытие (вырожденное) десятиугольник ({10/2}) с двумя наборами перекрывающихся вершин и ребер. Усеченный большой гептаграмма {7/3} дает тетрадекаграмма {14/3}.

Равномерное усечение в правильных многогранниках и мозаиках и выше

Усечения куба без возможности исправления

Когда «усечение» применяется к платоновые тела или же правильные мозаики, обычно подразумевается «равномерное усечение», что означает усечение до тех пор, пока исходные грани не станут правильными многоугольниками с вдвое большим количеством сторон, чем исходная форма.

Эта последовательность показывает пример усечения куба с использованием четырех шагов непрерывного процесса усечения между полными куб и исправленный куб. Последний многогранник - это кубооктаэдр. Среднее изображение - униформа усеченный куб; он представлен Символ Шлефли т{п,q,...}.

А битовое усечение - это более глубокое усечение, удаляющее все исходные края, но оставляющее внутреннюю часть исходных граней. Пример: а усеченный октаэдр представляет собой усеченный битами куб: t {3,4} = 2t {4,3}.

Полное усечение битов, называемое биректификация, уменьшает исходные грани до точек. Для многогранников это становится двойственный многогранник. Пример: октаэдр является двунаправленной куб: {3,4} = 2r {4,3}.

Другой тип усечения, песня, обрезает ребра и вершины, удаляя исходные ребра, заменяя их прямоугольниками, удаляя исходные вершины и заменяя их гранями двойственных исходных правильных многогранников или мозаик.

Многогранники более высокой размерности имеют более высокие усечения. Runcination разрезает грани, ребра и вершины. В 5 измерениях, стерилизация вырезает ячейки, грани и края.

Обрезка края

Обрезка краев куба, создание куб с фаской

Обрезка края это скашивание, или фаска для многогранников аналогично кантеллизу, но с сохранением исходных вершин и заменой ребер на шестиугольники. В 4-многогранниках при усечении ребер ребра заменяются на удлиненная бипирамида клетки.

Чередование или частичное усечение

Равномерное чередование усеченный кубооктаэдр дает неоднородный курносый куб.

При чередовании или частичном усечении удаляются только некоторые исходные вершины.

В частичное усечение, или же чередование, половина вершин и соединительные ребра удаляются полностью. Операция применима только к многогранникам с четными гранями. Количество граней уменьшается вдвое, а квадратные грани превращаются в ребра. Например, тетраэдр является альтернированным кубом h {4,3}.

Уменьшение это более общий термин, используемый в отношении Твердые тела Джонсона для удаления одной или нескольких вершин, ребер или граней многогранника, не затрагивая другие вершины. Например, трехуменьшенный икосаэдр начинается с регулярного икосаэдр с 3 удаленными вершинами.

Другие частичные усечения основаны на симметрии; например, тетраэдрически уменьшенный додекаэдр.

Обобщенные усечения

Типы усечений, показанные на край изолированы от большого многоугольника или многогранника с красными и синими вершинами. После полного усечения край меняет направление.

Процесс линейного усечения можно обобщить, допустив параметрические усечения, которые являются отрицательными или которые выходят за пределы средней точки ребер, вызывая самопересекающиеся звездчатые многогранники и могут параметрически относиться к некоторым из правильные звездные многоугольники и однородные звездные многогранники.

Мелкое усечение - Края уменьшены в длине, грани усечены, чтобы было вдвое больше сторон, а новые грани образуются с центрами в старых вершинах.
Равномерное усечение являются частным случаем этого с равными длинами кромок. В усеченный куб, t {4,3}, где квадратные грани становятся восьмиугольниками, а новые треугольные грани - вершинами.
Антивидение Обратный мелкое усечение, усеченная кнаружи от исходных краев, а не внутрь. Это приводит к многограннику, который выглядит как оригинал, но имеет части двойного, свисающие с его углов, вместо двойного врезания в его собственные углы.
Полное усечение или же исправление - Предел мелкого усечения, когда края сводятся к точкам. В кубооктаэдр, r {4,3}, является примером.
Гипертрофия Форма усечения, которая выходит за рамки исправления, инвертирует исходные края и вызывает появление самопересечений.
Квазиусечение Форма усечения, которая идет даже дальше, чем гипертрубка, когда перевернутая кромка становится длиннее, чем исходная кромка. Его можно сгенерировать из исходного многогранника, рассматривая все грани как ретроградные, то есть огибая вершину назад. Например, квазиусечение квадрат дает регулярный октаграмма (t {4,3} = {8/3}), и квазиусечение куб дает униформу звездчатый усеченный шестигранник, т {4 / 3,3}.

Усечения на квадрате
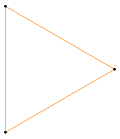
Типы усечения на квадрате, {4}, показывающие красные исходные края и новые усеченные края голубым цветом. Равномерно усеченный квадрат - это правильный восьмиугольник, t {4} = {8}. Полный усеченный квадрат становится новым квадратом с диагональной ориентацией. Вершины располагаются в порядке против часовой стрелки, 1-4, с усеченными парами вершин как а и б.

Усечения куба
⇨ т_аC	Куб {4,3} C	⇨ tC	Усечение т {4,3} tC	⇨ tC	Полное усечение г {4,3} AC	⇩ т_часC
Антивидение т_аC						Гипертрофия т_часC
⇧ т_аC	Полное квазиусечение а_qC	⇦	Квазиусечение т {4 / 3,3} т_qC	⇦ т_qC	Полное гипертрофирование а_часC	⇦ т_часC

Смотрите также

внешняя ссылка

Вайсштейн, Эрик В. «Усечение». MathWorld.
Ольшевский, Георгий. «Усечение». Глоссарий по гиперпространству. Архивировано из оригинал 4 февраля 2007 г.
Имена многогранников, усечение

Операторы многогранников
[
v
т
е
]
Семя	Усечение	Исправление	Bitruncation	Двойной	Расширение	Омнитуркация	Чередования


т₀{p, q} {p, q}	т₀₁{p, q} т {р, д}	т₁{p, q} г {р, д}	т₁₂{p, q} 2t {p, q}	т₂{p, q} 2r {p, q}	т₀₂{p, q} рр {р, q}	т₀₁₂{p, q} tr {p, q}	ht₀{p, q} ч {д, р}	ht₁₂{p, q} s {q, p}	ht₀₁₂{p, q} sr {p, q}