Правильный многогранник - Regular polytope

Примеры регулярных многогранников
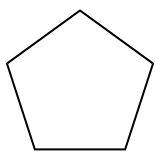Обычный пятиугольник это многоугольник, двумерный многогранник с 5 края, представлена Символ Шлефли {5}.	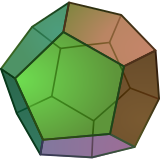Обычный додекаэдр это многогранник, трехмерный многогранник с 12-ю пятиугольниками. лица, представленный символом Шлефли {5,3}.
Обычный 120 ячеек это 4-многогранник, четырехмерный многогранник с 120 додекаэдрическими клетки, представленный символом Шлефли {5,3,3}. (показано здесь как Диаграмма Шлегеля )	Обычный кубические соты это мозаика, бесконечный трехмерный многогранник, представленный символом Шлефли {4,3,4}.
256 вершин и 1024 ребра 8-куб можно показать в этой ортогональной проекции (Многоугольник Петри )

В математика, а правильный многогранник это многогранник чей группа симметрии действует переходно на его флаги, тем самым придавая ему высшую степень симметрии. Все его элементы или j-лицы (для всех 0 ≤j ≤ п, куда п - размерность многогранника) - клетки, грани и т. д. - также транзитивны на симметриях многогранника и являются правильными многогранниками размерности ≤п.

Правильные многогранники являются обобщенным аналогом любого числа измерений правильные многоугольники (например, квадрат или правильный пятиугольник) и правильные многогранники (например, куб ). Сильная симметрия правильных многогранников дает им эстетический качество, которое интересует как нематематиков, так и математиков.

Классически правильный многогранник в п размеры могут быть определены как имеющие регулярные грани [(п - 1) -лицы] и правильные фигуры вершин. Этих двух условий достаточно, чтобы гарантировать, что все грани и все вершины одинаковы. Обратите внимание, однако, что это определение не работает для абстрактные многогранники.

Правильный многогранник можно представить в виде Символ Шлефли формы {a, b, c, ...., y, z}, с правильными гранями как {a, b, c, ..., y} и правильными фигурами вершин как {b, c, .. ., y, z}.

Классификация и описание

Правильные многогранники классифицируются в первую очередь по их размерности.

Их можно дополнительно классифицировать по симметрия. Например, куб и регулярный октаэдр обладают той же симметрией, что и обычные додекаэдр и икосаэдр. Действительно, группы симметрии иногда называют в честь правильных многогранников, например тетраэдрической и икосаэдрической симметрии.

В каждом измерении существуют три специальных класса регулярных многогранников:

В двух измерениях бесконечно много правильные многоугольники. В трех и четырех измерениях есть еще несколько правильные многогранники и 4-многогранники помимо этих трех. В пяти измерениях и выше они единственные. См. Также список правильных многогранников.

Идея многогранника иногда обобщается, чтобы включить связанные виды геометрических объектов. Некоторые из них имеют регулярные примеры, как обсуждается в разделе об исторических открытиях ниже.

Символы Шлефли

Краткое символическое представление правильных многогранников было разработано Людвигом. Schläfli в 19 веке, и слегка измененная форма стала стандартом. Обозначения лучше всего пояснять, добавляя по одному измерению за раз.

А выпуклый правильный многоугольник имея п стороны обозначается {п}. Итак, равносторонний треугольник - это {3}, квадрат {4} и так далее до бесконечности. Обычный звездный многоугольник который ветер м раз вокруг его центра обозначается дробным значением {п/м}, куда п и м находятся соправитель, так что регулярный пентаграмма составляет {5/2}.
А правильный многогранник имея лица {п} с п грани, соединяющиеся вокруг вершины, обозначаются {п, п}. Девять правильные многогранники являются {3, 3} {3, 4} {4, 3} {3, 5} {5, 3} {3, 5/2} {5/2, 3} {5, 5/2} и {5 / 2, 5}. {п} это вершина фигура многогранника.
Правильный 4-многогранник с ячейками {п, п} с q ячейки, соединяющиеся вокруг ребра, обозначаются {п, п, q}. Вершинная фигура 4-многогранника - это {п, q}.
Правильный 5-многогранник - это {п, п, q, р}. И так далее.

Двойственность правильных многогранников

В двойной регулярного многогранника также является правильным многогранником. Символ Шлефли для двойственного многогранника - это просто исходный символ, записанный в обратном направлении: {3, 3} самодвойственен, {3, 4} двойственен к {4, 3}, {4, 3, 3} к {3, 3, 4} и так далее.

В вершина фигура правильного многогранника является двойственным к его фасете. Например, фигура вершины {3, 3, 4} - это {3, 4}, двойственная к которой есть {4, 3} - a клетка из {4, 3, 3}.

В мера и перекрестные многогранники в любом измерении двойственны друг другу.

Если символ Шлефли палиндромный, т.е. читает одинаково вперед и назад, то многогранник самодвойственный. Самодвойственные правильные многогранники:

Все правильные многоугольники, {а}.
Все обычные п-симплексы, {3,3,...,3}
Регулярный 24-элементный в 4-х измерениях, {3,4,3}.
В отличный 120-элементный ({5,5 / 2,5}) и большой звездчатый 120-элементный ({5 / 2,5,5 / 2}) в 4-х измерениях.
Все обычные п-мерная кубическая соты, {4,3, ..., 3,4}. Их можно рассматривать как бесконечные многогранники.
Гиперболические мозаики и соты (мозаики {p, p} с p> 4 в 2 измерениях, {4,4,4}, {5,3,5}. {3,5,3}, {6,3,6}, и {3,6,3} в 3-х измерениях, {5,3,3,5} в 4-х измерениях и {3,3,4,3,3} в 5 измерениях).

Регулярные симплексы

Графики от 1-симплекса до 4-симплекса.

Отрезок	Треугольник	Тетраэдр	Пентахорон

Начни с точки А. Отметить точку B На расстоянии р из него и присоединиться, чтобы сформировать отрезок. Отметить точку C через секунду, ортогональный, размер на расстоянии р от обоих, и присоединиться к А и B сформировать равносторонний треугольник. Отметить точку D в третьем, ортогональном, измерении расстояние р из всех трех, и объединитесь, чтобы сформировать регулярный тетраэдр. И так далее для более высоких измерений.

Эти регулярные симплексы или же симплексы. Их имена в порядке размерности:

0. Точка

1. Отрезок

2. Равносторонний треугольник (обычный тригон)

3. Обычный тетраэдр

4. Обычный пентахорон или же 4-симплексный

5. Обычный гексатерон или же 5-симплекс

... п-simplex имеет п+1 вершина.

Многогранники с измерениями (гиперкубы)

Графики преобразования 2-куба в 4-куб.

Квадрат	Куб	Тессеракт

Начни с точки А. Продлить линию до точки B на расстоянии р, и соединитесь, чтобы сформировать линейный сегмент. Вытяните вторую линию длины р, ортогональный AB, из B к C, а также от А к D, чтобы сформировать квадрат ABCD. Продлите линии длины р соответственно от каждого угла, перпендикулярно обоим AB и до н.э (т.е. вверх). Отметить новые точки E,F,грамм,ЧАС сформировать куб ABCDEFGH. И так далее для более высоких измерений.

Эти измерять многогранники или же гиперкубы. Их имена в порядке размерности:

0. Балл

1. Отрезок линии

2. Квадрат (правильный четырехугольник)

3. Куб (правильный шестигранник)

4. Тессеракт (обычный октахорон) или же 4-куб

5. Penteract (обычный декатерон) или же 5-куб

... п-куб имеет 2^п вершины.

Кросс-многогранники (ортоплексы)

Графики от 2-ортоплекса до 4-ортоплекса.

Квадрат	Октаэдр	16 ячеек

Начни с точки О. Продлите линию в противоположных направлениях до точек А и B расстояние р из О и 2р Кроме. Нарисуйте линию COD длины 2р, сосредоточенный на О и ортогонален AB. Соедините концы, чтобы сформировать квадрат ACBD. Нарисуйте линию EOF такой же длины и с центром в 'O', ортогональный к AB и CD (т.е. вверх и вниз). Соедините концы с квадратом, чтобы сформировать правильный октаэдр. И так далее для более высоких измерений.

Эти перекрестные многогранники или же ортоплексы. Их имена в порядке размерности:

0. Балл

1. Отрезок линии

2. Квадрат (правильный четырехугольник)

3. Обычный октаэдр

4. Обычный гексадекахорон (16 ячеек ) или же 4-ортоплекс

5. Штатный триаконтакаидитерон (Пентакросс ) или же 5-ортоплекс

... п-ортоплекс имеет 2n вершины.

История открытия

Выпуклые многоугольники и многогранники

Самая ранняя из сохранившихся математических трактовок правильных многоугольников и многогранников пришла к нам из древнегреческий математики. Пятерка Платоновы тела были им известны. Пифагор знал по крайней мере о трех из них и Theaetetus (ок. 417 г. до н.э. - 369 г. до н.э.) описал все пять. Потом, Евклид написал систематическое исследование математики, опубликовав его под названием Элементы, которые построили логическую теорию геометрии и теория чисел. Его работа завершилась математическим описанием пяти Платоновы тела.

Платоновы тела

Тетраэдр	Куб	Октаэдр	Додекаэдр	Икосаэдр

Звездные многоугольники и многогранники

Наше понимание оставалось неизменным в течение многих столетий после Евклида. Дальнейшая история правильных многогранников может быть охарактеризована постепенным расширением основной концепции, позволяющей рассматривать все больше и больше объектов среди их числа. Томас Брэдвардин (Bradwardinus) был первым, кто провел серьезное исследование звездных многоугольников. В искусстве эпохи Возрождения появляются различные звездные многогранники, но только Иоганн Кеплер изучил малый звездчатый додекаэдр и большой звездчатый додекаэдр в 1619 году он понял, что эти двое были обычными. Луи Пуансо обнаружил большой додекаэдр и большой икосаэдр в 1809 г. и Огюстен Коши доказал, что список полон в 1812 году. Эти многогранники известны под общим названием Многогранники Кеплера-Пуансо.

Многогранники Кеплера-Пуансо

Маленький звездчатый додекаэдр	Большой звездчатый додекаэдр	Большой додекаэдр	Большой икосаэдр

Многомерные многогранники

Трехмерная проекция вращающегося тессеракта. Этот тессеракт изначально ориентирован так, чтобы все ребра были параллельны одной из четырех осей координатного пространства. Вращение происходит в плоскости xw.

Только в 19 веке швейцарский математик, Людвиг Шлефли, рассмотрел и охарактеризовал правильные многогранники в более высоких размерностях. Впервые его работы были полностью опубликованы в Шлефли (1901), шесть лет посмертно, хотя некоторые из них были опубликованы в Шлефли (1855) и Шлефли (1858). Между 1880 и 1900 годами результаты Шлефли были независимо открыты заново по крайней мере девятью другими математиками - см. Кокстер (1948, стр. 143–144). Больше подробностей. Шлефли назвал такую фигуру «полисхема» (по-английски «полисхема» или «полисхема»). Термин «многогранник» был введен Рейнхольд Хоппе, один из заново открывателей Шлефли, в 1882 году и впервые использованный на английском языке Алисия Буль Стотт лет двадцать спустя. Термин «многогранники» также использовался в более ранней литературе (Hilbert, 1952).

Кокстер (1948) вероятно, является наиболее полным печатным описанием результатов Шлефли и аналогичных результатов на сегодняшний день. Шлефли показал, что существует шесть правильные выпуклые многогранники в 4-х измерениях. Пять из них можно рассматривать как аналог Платоновых тел: 4-симплексный (или пентахорон) к тетраэдр, то гиперкуб (или же тессеракт ) к куб, то 4-ортоплекс (или гексадекахорон, или 16 ячеек ) к октаэдр, то 120 ячеек к додекаэдр, а 600 ячеек к икосаэдр. Шестой, 24-элементный, можно рассматривать как переходную форму между гиперкубом и 16-ячейками, аналогично тому, как кубооктаэдр и ромбический додекаэдр являются переходными формами между кубом и октаэдром.

В пяти и более измерениях есть ровно три правильных многогранника, которые соответствуют тетраэдру, кубу и октаэдру: это регулярные симплексы, измерять многогранники и перекрестные многогранники. Их описания можно найти в список правильных многогранников. Также представляют интерес звезды правильные 4-многогранники, частично обнаруженный Шлефли.

К концу XIX века такие математики, как Артур Кэли и Людвиг Шлефли разработал теорию правильных многогранников в четырех и более измерениях, таких как тессеракт и 24-элементный.

Последние трудно (хотя и возможно) визуализировать, но они все же сохраняют эстетически приятную симметрию своих собратьев из более низких измерений. В тессеракт содержит 8 кубических ячеек. Он состоит из двух кубов в параллельных гиперплоскостях с соответствующими вершинами, перекрестно соединенными таким образом, что 8 поперечных ребер равны по длине и ортогональны 12 + 12 ребрам, расположенным на каждом кубе. Соответствующие грани двух кубиков соединяются, образуя оставшиеся 6 кубических граней куба. тессеракт. В 24-элементный может быть получено из тессеракт путем соединения 8 вершин каждой из его кубических граней с дополнительной вершиной, чтобы сформировать четырехмерный аналог пирамиды. Обе фигуры, как и другие 4-х мерные фигуры, могут быть непосредственно визуализированы и изображены с помощью 4-х мерных стереографов.^[1]

Еще труднее представить, что они более современные абстрактные правильные многогранники такой как 57 ячеек или 11-элементный. Однако с математической точки зрения эти объекты обладают теми же эстетическими качествами, что и их более знакомые двух- и трехмерные родственники.

В начале ХХ века определение правильного многогранника было следующим.

Правильный многоугольник - это многоугольник, у которого все стороны равны и все углы равны.
Правильный многогранник - это многогранник, все грани которого являются конгруэнтными правильными многоугольниками, а фигуры вершин все конгруэнтны и правильны.
И так далее, обычный п-полигон п-мерный многогранник, у которого (п - 1) -мерные грани все правильные и конгруэнтные, а фигуры вершин все правильные и конгруэнтные.

Это «рекурсивное» определение. Он определяет правильность фигур более высоких размеров относительно правильных фигур более низкого измерения. Существует эквивалентное (нерекурсивное) определение, в котором говорится, что многогранник является регулярным, если он имеет достаточную степень симметрии.

An п-многогранник является правильным, если любой набор, состоящий из вершины, содержащего ее ребра, двумерной грани, содержащей ребро, и т. д. до п−1 размерность, может быть отображена в любой другой такой набор симметрией многогранника.

Так, например, куб является правильным, потому что если мы выберем вершину куба, одно из трех ребер, на котором он находится, и одну из двух граней, содержащих ребро, тогда эта тройка, или флаг, (вершина, ребро, грань) можно отобразить на любой другой такой флаг с помощью подходящей симметрии куба. Таким образом, мы можем очень кратко определить правильный многогранник:

Правильный многогранник - это многогранник, группа симметрии которого транзитивна по флагам.

В 20-м веке были сделаны некоторые важные события. В симметрия группы классических правильных многогранников были обобщены в то, что теперь называется Группы Кокстера. К группам Кокстера относятся также группы симметрии регулярных мозаика космоса или плоскости. Например, группа симметрии бесконечного шахматная доска будет группой Кокстера [4,4].

Апейотопы - бесконечные многогранники

В первой половине 20 века Кокстер и Петри открыли три бесконечные структуры {4, 6}, {6, 4} и {6, 6}. Они назвали их правильными косыми многогранниками, потому что они, казалось, удовлетворяли определению правильного многогранника - все вершины, ребра и грани одинаковы, все углы одинаковы, и фигура не имеет свободных ребер. В настоящее время их называют бесконечными многогранниками или апейроэдрами. Правильные мозаики плоскости {4, 4}, {3, 6} и {6, 3} также можно рассматривать как бесконечные многогранники.

В 1960-е годы Бранко Грюнбаум обратился к геометрическому сообществу с призывом рассмотреть более абстрактные типы правильных многогранников, которые он назвал полистроматы. Он разработал теорию полистромат, показывая примеры новых объектов, которые он назвал обычные апейротопы, т.е. правильные многогранники с бесконечно много лиц. Простой пример косой апейрогон будет зигзагом. Кажется, он удовлетворяет определению правильного многоугольника - все ребра одинаковой длины, все углы одинаковы, и у фигуры нет свободных концов (потому что они никогда не достижимы). Что еще более важно, возможно, существуют симметрии зигзага, которые могут отображать любую пару вершины и присоединенного ребра к любой другой. С тех пор продолжали открываться другие обычные апейрогоны и высшие апейротопы.

Правильные сложные многогранники

А комплексное число имеет действительную часть, с которой мы все знакомы, и мнимую часть, кратную квадратному корню из минус единицы. Комплекс Гильбертово пространство имеет координаты x, y, z и т. д. в виде комплексных чисел. Это фактически удваивает количество измерений. Многогранник, построенный в таком унитарном пространстве, называется многогранником. сложный многогранник.^[2]

Абстрактные многогранники

В Hemicube получается из куба приравниванием противоположных вершин, ребер и граней. У него 4 вершины, 6 ребер и 3 грани.

Грюнбаум также открыл 11-элементный, четырехмерный самодвойственный объект, грани которого не являются икосаэдрами, а являются «полуикосаэдрами» - то есть они представляют собой форму, которую можно получить, если рассматривать противоположные грани икосаэдров как фактически одно и тоже лицо (Грюнбаум 1976 ). У полуикосаэдра всего 10 треугольных граней и 6 вершин, в отличие от икосаэдра, у которого их 20 и 12.

Читателю будет легче понять эту концепцию, если учесть взаимосвязь куба и полукуба. У обычного куба 8 углов, их можно обозначить буквами от A до H, где A напротив H, B напротив G и т. Д. В гемикубе A и H будут рассматриваться как один и тот же угол. Так было бы с B и G и так далее. Ребро AB станет тем же ребром, что и GH, а грань ABEF станет той же гранью, что и CDGH. У новой формы всего три грани, 6 граней и 4 угла.

11-ячейка не может быть сформирована с помощью регулярной геометрии в плоском (евклидовом) гиперпространстве, а только в положительно искривленном (эллиптическом) гиперпространстве.

Через несколько лет после открытия Грюнбаумом 11-элементный, Х. С. М. Коксетер независимо открыл ту же форму. Ранее он обнаружил подобный многогранник 57 ячеек (Coxeter 1982, 1984).

К 1994 году Грюнбаум абстрактно рассматривал многогранники как комбинаторные множества точек или вершин, и его не волновало, были ли грани плоскими. По мере того как он и другие уточняли эти идеи, такие наборы стали называть абстрактные многогранники. Абстрактный многогранник определяется как частично упорядоченное множество (poset), элементами которого являются грани многогранника (вершины, ребра, грани и т. Д.), Упорядоченные по сдерживание. На множество накладываются определенные ограничения, аналогичные свойствам, которым удовлетворяют классические регулярные многогранники (включая Платоновы тела). Однако ограничения достаточно жесткие, чтобы регулярные мозаики, полукубы и даже такие странные объекты, как 11-элементный или чужой, были примерами правильных многогранников.

Под геометрическим многогранником понимается реализация абстрактного многогранника, так что существует взаимно однозначное отображение абстрактных элементов в геометрические. Таким образом, любой геометрический многогранник может быть описан соответствующим абстрактным множеством, хотя не все абстрактные многогранники имеют правильные геометрические реализации.

С тех пор теория получила дальнейшее развитие, в основном Макмаллен и Шульте (2002), но другие исследователи также внесли свой вклад.

Регулярность абстрактных многогранников

Регулярность имеет родственное, хотя и разное значение для абстрактные многогранники, поскольку углы и длины ребер значения не имеют.

Определение регулярности в терминах транзитивности флагов, данное во введении, применимо к абстрактным многогранникам.

Любой классический регулярный многогранник имеет абстрактный регулярный эквивалент, полученный взятием множества граней. Но нерегулярные классические многогранники могут иметь обычные абстрактные эквиваленты, поскольку абстрактные многогранники, например, не заботятся об углах и длинах ребер. А правильный абстрактный многогранник не может быть реализован как классический многогранник.

Все полигоны являются регулярными, например, в абстрактном мире, тогда как в классическом мире правильными являются только те, которые имеют равные углы и равные длины ребер.

Вершинная фигура абстрактных многогранников

Концепция чего-либо вершина фигура также по-другому определяется для абстрактный многогранник. Фигура вершины данного абстракта п-многогранник в данной вершине V это набор всех абстрактных лиц, которые содержат V, включая V сам. Более формально это абстрактный раздел.

F_п / V = {F | V ≤ F ≤ F_п}

куда F_п - максимальная грань, т.е. условное п-лицо, которое содержит все остальные лица. Обратите внимание, что каждый я-лицо, я ≥ 0 исходного многогранника становится (я - 1) -грань вершинной фигуры.

В отличие от евклидовых многогранников, абстрактный многогранник с правильными гранями и фигурами вершин может или не может быть правильной сама по себе - например, квадратная пирамида, все грани и вершины которой являются правильными абстрактными многоугольниками.

Однако классическая вершинная фигура будет реализацией абстрактной.

Конструкции

Полигоны

Традиционный способ построить правильный многоугольник или любую другую фигуру на плоскости - это компас и линейка. Построить некоторые правильные многоугольники таким способом очень просто (самый простой - это, возможно, равносторонний треугольник), некоторые более сложные, а некоторые невозможны («не построены»). Самые простые правильные многоугольники, которые невозможно построить, - это п-сторонние многоугольники с п равно 7, 9, 11, 13, 14, 18, 19, 21, ...

Конструктивность в этом смысле относится только к идеальным конструкциям с идеальными инструментами. Конечно, достаточно точные приближения можно построить с помощью ряда методов; в то время как теоретически возможные конструкции могут оказаться непрактичными.

Многогранники

Евклида Элементы сколько дал построений линейки и циркуля для пяти Платоновых тел.^[3] Однако чисто практический вопрос о том, как можно провести прямую линию в пространстве даже с помощью линейки, может привести к сомнению, что именно означает «построить» правильный многогранник. (Конечно, можно задать тот же вопрос о многоугольниках.)

Сеть за икосаэдр

Английское слово «construct» означает систематическое построение конструкции. Самый распространенный способ построения правильного многогранника - это складная сетка. Чтобы получить разворачивающуюся сетку многогранника, нужно взять поверхность многогранника и разрезать ее вдоль ровно столько краев, чтобы поверхность могла быть плоской. Это дает план сети развернутого многогранника. Поскольку у Платоновых тел есть только треугольники, квадраты и пятиугольники для лиц, и все они могут быть построены с помощью линейки и циркуля, существуют методы линейки и компаса для рисования этих складывающихся сетей. То же самое относится и к звездным многогранникам, хотя здесь мы должны быть осторожны, чтобы сделать сетку только для видимой внешней поверхности.

Если эта сетка нарисована на картоне или подобном складывающемся материале (например, листовом металле), сетку можно вырезать, сложить вдоль неразрезанных краев, соединить по соответствующим обрезанным краям и таким образом сформировать многогранник, для которого сетка была разработан. Для данного многогранника может быть много раскладывающихся сеток. Например, для куба их 11, а для додекаэдра - более 900000.^[4]

Многочисленные детские игрушки, обычно предназначенные для подростков или подростков, позволяют экспериментировать с правильными многоугольниками и многогранниками. Например, Klikko предлагает наборы пластиковых треугольников, квадратов, пятиугольников и шестиугольников, которые можно соединить по стыку большим количеством различных способов. Ребенок, играющий с такой игрушкой, может заново открыть для себя Платоновы твердые тела (или Архимедовы тела ), особенно если получить небольшой совет со стороны знающего взрослого.

Теоретически для построения правильных многогранников можно использовать практически любой материал.^[5] Их можно вырезать из дерева, вылепить из проволоки, сформировать из цветного стекла. Воображение - это предел.

Высшие измерения

Сеть за тессеракт

Перспективная проекция (Диаграмма Шлегеля ) для тессеракта

Анимированный разрез в разрезе 24-элементный.

В более высоких измерениях становится труднее сказать, что подразумевается под «конструированием» объектов. Очевидно, что в трехмерной Вселенной невозможно построить физическую модель объекта, имеющего 4 или более измерений. Есть несколько подходов, которые обычно используются для решения этой проблемы.

Первый подход, подходящий для четырех измерений, использует четырехмерную стереографию.^[1] Глубина в третьем измерении представлена горизонтальным относительным смещением, глубина в четвертом измерении - вертикальным относительным смещением между левым и правым изображениями стереографа.

Второй подход заключается во встраивании многомерных объектов в трехмерное пространство с использованием методов, аналогичных способам рисования трехмерных объектов на плоскости. Например, раскладывающиеся сети, упомянутые в предыдущем разделе, имеют эквиваленты более высоких измерений.^[6] Можно даже представить себе создание модели этой разворачивающейся сети, как нарисовать разворачивающуюся сетку многогранника на листе бумаги. К сожалению, из-за ограничений физической вселенной мы никогда не смогли выполнить необходимое сворачивание трехмерной структуры для получения четырехмерного многогранника. Другой способ «нарисовать» многомерные формы в 3-х измерениях - использовать какую-то проекцию, например, аналог любого орфографический или же перспектива проекция. Знаменитая книга Кокстера о многогранниках (Кокстер 1948 ) есть несколько примеров таких орфографических проекций.^[7] Обратите внимание, что погружение даже четырехмерной полихоры непосредственно в два измерения довольно запутано. Легче понять трехмерные модели прогнозов. Такие модели иногда можно найти в научных музеях или на математических факультетах университетов (например, Université Libre de Bruxelles ).

Пересечение четырехмерного (или более высокого) правильного многогранника с трехмерной гиперплоскостью будет многогранником (не обязательно правильным). Если гиперплоскость перемещается по фигуре, трехмерные срезы можно объединить, анимированный в своего рода четырехмерный объект, где четвертое измерение принято за время. Таким образом, мы можем увидеть (если не полностью понять) полную четырехмерную структуру четырехмерных регулярных многогранников через такие разрезы. Это аналогично тому, как Томография повторно собирает двухмерные изображения, чтобы сформировать трехмерное представление сканируемых органов. Идеальным был бы анимационный голограмма в некотором роде, однако, даже простая анимация, подобная показанной, уже может дать некоторое ограниченное представление о структуре многогранника.

Другой способ, которым трехмерный наблюдатель может понять структуру четырехмерного многогранника, - это "погружение" в объект, возможно, посредством какой-либо формы виртуальная реальность технологии. Чтобы понять, как это может работать, представьте, что можно было бы увидеть, если бы пространство было заполнено кубиками. Зритель будет внутри одного из кубов и сможет видеть кубики спереди, сзади, сверху, снизу, слева и справа от себя. Если бы можно было путешествовать в этих направлениях, можно было бы исследовать массив кубов и понять его геометрическую структуру. An бесконечный массив кубиков не является многогранником в традиционном смысле. По сути, это мозаика 3-х мерного (Евклидово ) Космос. Однако 4-многогранник можно рассматривать как тесселяцию трехмерного неевклидов пространство, а именно мозаика поверхности четырехмерного сфера (4-мерный сферическая черепица ).

Обычные додекаэдрические соты, {5,3,4}, гиперболического пространства, спроецированного в 3-пространство.

Локально это пространство похоже на то, с которым мы знакомы, и поэтому система виртуальной реальности в принципе может быть запрограммирована так, чтобы позволить исследование этих «мозаик», то есть четырехмерных правильных многогранников. Кафедра математики в г. UIUC есть несколько изображений того, что можно было бы увидеть, если бы они были встроены в мозаика из гиперболическое пространство с додекаэдрами. Такая мозаика образует пример бесконечного абстрактного правильного многогранника.

Обычно для абстрактных правильных многогранников математик считает, что объект «построен», если структура его группа симметрии известен. Это происходит из-за важной теоремы в изучении абстрактных регулярных многогранников, предоставляющей технику, которая позволяет строить абстрактный регулярный многогранник по его группе симметрии стандартным и простым способом.

Правильные многогранники в природе

Примеры полигонов в природе см.

Каждое из Платоновых тел встречается в природе в той или иной форме:

Смотрите также

внешняя ссылка

Ольшевский, Георгий. «Правильный многогранник». Глоссарий по гиперпространству. Архивировано из оригинал 4 февраля 2007 г.
Атлас малых регулярных многогранников - Список абстрактных правильных многогранников.

Фундаментальный выпуклый обычный и однородные многогранники в размерах 2–10
Семья	А_п	B_п	я₂(п) / D_п	E₆ / E₇ / E₈ / F₄ / грамм₂	ЧАС_п
Правильный многоугольник	Треугольник	Квадрат	п-угольник	Шестиугольник	Пентагон
Равномерный многогранник	Тетраэдр	Октаэдр • Куб	Демикуб		Додекаэдр • Икосаэдр
Равномерный 4-многогранник	5-элементный	16 ячеек • Тессеракт	Demitesseract	24-элементный	120 ячеек • 600 ячеек
Равномерный 5-многогранник	5-симплекс	5-ортоплекс • 5-куб	5-полукуб
Равномерный 6-многогранник	6-симплекс	6-ортоплекс • 6-куб	6-полукуб	1₂₂ • 2₂₁
Равномерный 7-многогранник	7-симплекс	7-ортоплекс • 7-куб	7-полукуб	1₃₂ • 2₃₁ • 3₂₁
Равномерный 8-многогранник	8-симплекс	8-ортоплекс • 8-куб	8-полукруглый	1₄₂ • 2₄₁ • 4₂₁
Равномерный 9-многогранник	9-симплекс	9-ортоплекс • 9-куб	9-полукуб
Равномерный 10-многогранник	10-симплекс	10-ортоплекс • 10-куб	10-полукуб
Униформа п-многогранник	п-симплекс	п-ортоплекс • п-куб	п-полукуб	1_k2 • 2_k1 • k₂₁	п-пятиугольный многогранник
Темы: Семейства многогранников • Правильный многогранник • Список правильных многогранников и соединений

[Brisson-1] а ^б Бриссон, Дэвид В. (2019) [1978]. «Визуальное восприятие в n-измерениях». В Бриссоне, Дэвид В. (ред.). Гиперграфика: визуализация сложных отношений в искусстве, науке и технологиях. Избранный симпозиум AAAS. 24. Тейлор и Фрэнсис. С. 109–145. ISBN 978-0-429-70681-3.

[2] Кокстер (1974)

[3] См., Например, Элементы Евклида.

[4] Доступны интересные раскладывающиеся сети куба, октаэдра, додекаэдра и икосаэдра. Вот.

[5] Инструкции по сборке оригами модели могут быть найдены Вот, Например.

[6] Некоторые из них можно посмотреть на [1].

[7] Другие примеры можно найти в Интернете (см., Например, [2] ).

[1]

[2]

[3]

[4]

[5]

[6]

[7]