Равномерный 4-многогранник - Uniform 4-polytope

Диаграмма Шлегеля для усеченный 120-ячеечный с участием четырехгранный видимые ячейки

Ортографическая проекция усеченной 120-ячейки, в H₃ Самолет Кокстера (D₁₀ симметрия). Рисуются только вершины и ребра.

В геометрия, а униформа 4-многогранник (или равномерный полихорон)^[1] является 4-мерным многогранник который вершинно-транзитивный и чьи клетки равномерные многогранники, а лица правильные многоугольники.

Описаны 47 непризматических выпуклых равномерных 4-многогранников, один конечный набор выпуклых призматических форм и два бесконечных набора выпуклых призматических форм. Также неизвестно количество невыпуклых звездных форм.

История открытия

Выпуклый Правильные многогранники:
- 1852: Людвиг Шлефли доказано в его рукописи Theorie der vielfachen Kontinuität что правильных многогранников в 4 Габаритные размеры и только 3 в 5 или более измерениях.
Правильные звездные 4-многогранники (звездный многогранник клетки и / или фигуры вершин )
- 1852: Людвиг Шлефли также нашел 4 из 10 правильных звездных 4-многогранников, исключая 6 с ячейками или вершинами {⁵/₂,5} и {5,⁵/₂}.
- 1883: Эдмунд Гесс завершил список из 10 невыпуклых правильных 4-многогранников в своей книге (на немецком языке) Einleitung in die Lehre von der Kugelteilung mit besonderer Berücksichtigung ihrer Anwendung auf die Theorie der Gleichflächigen und der gleicheckigen Polyeder [2].
Выпуклый полуправильные многогранники: (Различные определения до Кокстера униформа категория)
- 1900: Торольд Госсет перечислил список непризматических полуправильных выпуклых многогранников с правильными ячейками (Платоновы тела ) в своей публикации О регулярных и полурегулярных фигурах в пространстве n измерений.^[2]
- 1910: Алисия Буль Стотт, в своей публикации Геометрическое выведение полуправильных из правильных многогранников и заполнения пространств, расширили определение, также разрешив Архимедово твердое тело и призма клетки. Эта конструкция перечислила 45 полуправильных 4-многогранников.^[3]
- 1911: Питер Хендрик Шуте опубликовано Аналитическая обработка многогранников, регулярно получаемых из правильных многогранников, следуя обозначениям Буля-Стотта, перечисляя выпуклые равномерные многогранники симметрией, основанной на 5-элементный, 8-элементный /16 ячеек, и 24-элементный.
- 1912: Э. Л. Элте независимо расширили список Госсета публикацией Полурегулярные многогранники гиперпространств, многогранники с одним или двумя типами полурегулярных граней.^[4]
Выпуклые равномерные многогранники:
- 1940: Поиск был систематически расширен H.S.M. Coxeter в своей публикации Правильные и полурегулярные многогранники.
- Выпуклые равномерные 4-многогранники:
  - 1965: Полный список выпуклых форм окончательно перечислил Джон Хортон Конвей и Майкл Гай в своей публикации Четырехмерные архимедовы многогранники, установленный с помощью компьютерного анализа, добавив только один невыпуклый 4-многогранник, не являющийся Витофовым, великая антипризма.
  - 1966 Норман Джонсон имеет степень доктора философии. диссертация Теория однородных многогранников и сот под руководством Кокстера завершает основную теорию однородных многогранников для размерностей 4 и выше.
  - 1986 Кокстер опубликовал статью Правильные и полурегулярные многогранники II который включал анализ уникальных курносый 24-элементный структура и симметрия аномальной большой антипризмы.
  - 1998^[5]-2000: 4-многогранники были систематически названы Норманом Джонсоном и даны индексированным онлайн-списком Джорджа Ольшевского (использованным в качестве основы для этого списка). Джонсон назвал 4-многогранники полихорами, как многогранники для 3-многогранников, из Греческий корни поли («многие») и хоро («комната» или «пространство»).^[6] Названия единой полихоры начинались с 6 правильных полихор с приставками, основанными на кольцах в диаграммах Кокстера; усечение t_0,1, песня, т_0,2, runcination t_0,3, с одинарными кольцевыми формами, называемыми ректифицированными, и би, тройными префиксами, добавленными, когда первое кольцо было на втором или третьем узлах.^[7]^[8]
  - 2004: Доказательство полноты множества Конвея-Гая было опубликовано Марко Мёллером в его диссертации, Vierdimensionale Archimedische Polytope. Мёллер воспроизвел систему именования Джонсона в своем списке.^[9]
  - 2008: Симметрии вещей^[10] был опубликован Джон Х. Конвей и содержит первый опубликованный в печати список выпуклых равномерных 4-многогранников и многогранников большей размерности по семейству групп Кокстера с общими вершина фигуры диаграммы для каждого окольцованного Диаграмма Кокстера перестановка - курносый, великая антипризма и дуопризма, - которые он назвал пропризмами для продуктовых призм. Он использовал свой ijk-ambo схема именования для индексированных перестановок кольца помимо усечения и усечения битов, и все имена Джонсона были включены в указатель книги.
Нерегулярные однородные звездные 4-многогранники: (аналогично невыпуклые равномерные многогранники )
- 2000-2005: В ходе совместного поиска до 2005 года Джонатаном Бауэрсом и Джорджем Ольшевским было идентифицировано 1845 однородных 4-многогранников (выпуклых и невыпуклых).^[11], и еще четыре были обнаружены в 2006 году, всего на сегодняшний день известно 1849.^[12]

Правильные 4-многогранники

Правильные 4-многогранники являются подмножеством равномерных 4-многогранников, удовлетворяющих дополнительным требованиям. Правильные 4-многогранники можно выразить с помощью Символ Шлефли {п,q,р} имеют ячейки типа {п,q}, лица типа {п}, фигурные края {р}, и фигуры вершин {q,р}.

Существование правильного 4-многогранника {п,q,р} ограничивается существованием правильных многогранников {п,q} который становится клетками, и {q,р} который становится вершина фигуры.

Существование конечного 4-многогранника зависит от неравенства:^[13]

{ displaystyle sin left ({ frac { pi} {p}} right) sin left ({ frac { pi} {r}} right)> cos left ({ frac { pi} {q}} right).}

16 правильные 4-многогранники, с тем свойством, что все ячейки, грани, ребра и вершины конгруэнтны:

6 правильные выпуклые 4-многогранники: 5-элементный {3,3,3}, 8-элементный {4,3,3}, 16 ячеек {3,3,4}, 24-элементный {3,4,3}, 120 ячеек {5,3,3}, и 600 ячеек {3,3,5}.
10 правильные звездные 4-многогранники: икосаэдрический 120-элементный {3,5,⁵/₂}, маленький звездчатый 120-элементный {⁵/₂,5,3}, отличный 120-элементный {5,⁵/₂,5}, большой 120-элементный {5,3,⁵/₂}, большой звездчатый 120-элементный {⁵/₂,3,5}, большой звездчатый 120-элементный {⁵/₂,5,⁵/₂}, великий гранд 120-элементный {5,⁵/₂,3}, большой икосаэдр, 120 ячеек {3,⁵/₂,5}, большой 600-элементный {3,3,⁵/₂}, и большой звездчатый 120-элементный {⁵/₂,3,3}.

Выпуклые равномерные 4-многогранники

Симметрия однородных 4-многогранников в четырех измерениях

Ортогональные подгруппы
16 зеркал B₄ можно разложить на 2 ортогональные группы, 4А₁ и D₄: = (4 зеркала) = (12 зеркал)
24 зеркала F₄ можно разложить на 2 ортогональных D₄ группы: = (12 зеркал) = (12 зеркал)
10 зеркал B₃×А₁ можно разложить на ортогональные группы, 4А₁ и D₃: = (3 + 1 зеркала) = (6 зеркал)

Есть 5 фундаментальных зеркальных симметрий точечная группа семьи в 4-х измерениях: А₄ = , B₄ = , D₄ = , F₄ = , ЧАС₄ = .^[7] Также есть 3 призматические группы А₃А₁ = , B₃А₁ = , ЧАС₃А₁ = , и дуопризматические группы: I₂(p) × I₂(q) = . Каждая группа определяется Тетраэдр Гурса фундаментальная область ограничен зеркальными плоскостями.

Каждый отражающий однородный 4-многогранник может быть построен в одной или нескольких группах отражающих точек в четырех измерениях с помощью Строительство Wythoff, представленный кольцами вокруг перестановок узлов в Диаграмма Кокстера. Зеркало гиперплоскости могут быть сгруппированы по цветным узлам, разделенным четными ветвями. Группы симметрии вида [a, b, a] обладают расширенной симметрией [[a, b, a]], удваивающей порядок симметрии. Сюда входят [3,3,3], [3,4,3] и [п,2,п]. Равномерные многогранники в этой группе с симметричными кольцами содержат эту расширенную симметрию.

Если в данном однородном многограннике все зеркала данного цвета не закручены (неактивны), он будет иметь конструкцию с более низкой симметрией, удалив все неактивные зеркала. Если все узлы данного цвета обведены (активны), чередование операция может сгенерировать новый 4-многогранник с киральной симметрией, показанный как «пустые» обведенные узлы », но геометрия обычно не регулируется для создания однородных решений.

Weyl группа	Конвей Кватернион	Абстрактные структура	порядок	Coxeter обозначение	Коммутатор подгруппа	Coxeter количество (час)	Зеркала м=2час
Неприводимый
А₄	+1/60 [I × I] .21	S₅	120	[3,3,3]	[3,3,3]⁺	5		10
D₄	± 1/3 [Т × Т] .2	1/2.²S₄	192	[3^1,1,1]	[3^1,1,1]⁺	6		12
B₄	± 1/6 [O × O] .2	²S₄ = S₂≀S₄	384	[4,3,3]	[3^1,1,1]⁺	8	4	12
F₄	± 1/2 [O × O] .2₃	3.²S₄	1152	[3,4,3]	[3⁺,4,3⁺]	12	12	12
ЧАС₄	± [I × I] .2	2. (А₅× А₅).2	14400	[5,3,3]	[5,3,3]⁺	30		60
Призматические группы
А₃А₁	+1/24 [O × O] .2₃	S₄× D₁	48	[3,3,2] = [3,3]×[ ]	[3,3]⁺	-		6	1
B₃А₁	± 1/24 [O × O] .2	S₄× D₁	96	[4,3,2] = [4,3]×[ ]	[3,3]⁺	-	3	6	1
ЧАС₃А₁	± 1/60 [I × I] .2	А₅× D₁	240	[5,3,2] = [5,3]×[ ]	[5,3]⁺	-		15	1
Дуопризматические группы (используйте 2p, 2q для четных целых чисел)
я₂(п)Я₂(q)	± 1/2 [D_2п× D_2q]	D_п× D_q	4pq	[п,2,q] = [п]×[q]	[п⁺,2,q⁺]	-		п	q
я₂(2p)Я₂(q)	± 1/2 [D_4п× D_2q]	D_2п× D_q	8pq	[2п,2,q] = [2п]×[q]		-	п	п	q
я₂(2p)Я₂(2кв.)	± 1/2 [D_4п× D_4q]	D_2p× D_2кв.	16pq	[2п,2,2q] = [2п]×[2q]		-	п	п	q	q

Перечисление

Имеется 64 выпуклых равномерных 4-многогранника, в том числе 6 правильных выпуклых 4-многогранников, исключая бесконечные множества дуопризма и антипризматические призмы.

5 - многогранные призмы на основе Платоновы тела (1 перекрывается с регулярным, так как кубическая гиперпризма тессеракт )
13 - многогранные призмы на основе Архимедовы тела
9 находятся в автодуальной регулярной A₄ [3,3,3] группа (5-элементный ) семья.
9 находятся в автодуальной регулярной F₄ [3,4,3] группа (24-элементный ) семья. (Исключая курносый 24-элементный)
15 находятся в обычном B₄ [3,3,4] группа (тессеракт /16 ячеек ) семья (3 пересечения с 24-элементной семьей)
15 находятся в обычном H₄ [3,3,5] группа (120 ячеек /600 ячеек ) семья.
1 специальная курносая форма в группе [3,4,3] (24-элементный ) семья.
1 специальный не-Wythoffian 4-многогранник, большая антипризма.
ИТОГО: 68 - 4 = 64

Эти 64 равномерных 4-многогранника проиндексированы ниже Георгием Ольшевским. В скобках указаны повторяющиеся формы симметрии.

В дополнение к 64 выше, есть 2 бесконечных призматических набора, которые генерируют все оставшиеся выпуклые формы:

Набор из однородные антипризматические призмы - sr {п, 2} × {} - многогранные призмы двух антипризмы.
Комплект униформы дуопризма - {п}×{q} - А Декартово произведение из двух полигонов.

А₄ семья

5-элементный диплоидный пентахорический [3,3,3] симметрия,^[7] из порядок 120, изоморфный перестановкам пяти элементов, потому что все пары вершин связаны одинаковым образом.

Даны фасеты (ячейки), сгруппированные в их положениях диаграммы Кокстера путем удаления указанных узлов.

[3,3,3] равномерные многогранники
#	имя	Вершина фигура	Диаграмма Кокстера и Schläfli символы	Подсчет клеток по местоположению				Количество элементов
#	имя	Вершина фигура	Диаграмма Кокстера и Schläfli символы	Поз. 3 (5)	Поз. 2 (10)	Поз. 1 (10)	Поз. 0 (5)	Клетки	Лица	Края	Вершины
1	5-элементный пентахорон^[7]		{3,3,3}	(4) (3.3.3)				5	10	10	5
2	выпрямленный 5-элементный		г {3,3,3}	(3) (3.3.3.3)			(2) (3.3.3)	10	30	30	10
3	усеченный 5-элементный		т {3,3,3}	(3) (3.6.6)			(1) (3.3.3)	10	30	40	20
4	скошенный 5-элементный		рр {3,3,3}	(2) (3.4.3.4)		(2) (3.4.4)	(1) (3.3.3.3)	20	80	90	30
7	усеченный 5-элементный		tr {3,3,3}	(2) (4.6.6)		(1) (3.4.4)	(1) (3.6.6)	20	80	120	60
8	усеченный 5-элементный		т_0,1,3{3,3,3}	(1) (3.6.6)	(2) (4.4.6)	(1) (3.4.4)	(1) (3.4.3.4)	30	120	150	60

[[3,3,3]] равномерные многогранники
#	имя	Вершина фигура	Диаграмма Кокстера и Schläfli символы	Подсчет клеток по местоположению			Количество элементов
#	имя	Вершина фигура	Диаграмма Кокстера и Schläfli символы	Поз. 3-0 (10)	Поз. 1-2 (20)	Alt	Клетки	Лица	Края	Вершины
5	*5-клеточный		т_0,3{3,3,3}	(2) (3.3.3)	(6) (3.4.4)		30	70	60	20
6	*усеченный по битам 5-элементный декахорон		2т {3,3,3}	(4) (3.6.6)			10	40	60	30
9	*омниусеченный 5-элементный		т_0,1,2,3{3,3,3}	(2) (4.6.6)	(2) (4.4.6)		30	150	240	120
Неоднородный	омниснуб 5-элементный^[14]		ht_0,1,2,3{3,3,3}	(2) (3.3.3.3.3)	(2) (3.3.3.3)	(4) (3.3.3)	90	300	270	60

Формы трех однородных 4-многогранников, отмеченные знаком звездочка, *, иметь высшее расширенная пентахорическая симметрия, порядка 240, [[3,3,3]], поскольку элемент, соответствующий любому элементу базовой 5-ячейки, может быть заменен одним из элементов, соответствующих элементу его двойственного элемента. Есть одна небольшая индексная подгруппа [3,3,3]⁺, порядок 60 или его удвоение [[3,3,3]]⁺, порядок 120, определяющий омниснуб 5-элементный который указан для полноты, но не является единообразным.

B₄ семья

В этой семье есть диплоидный гексадекахорический симметрия,^[7] [4,3,3], из порядок 24 × 16 = 384: 4! = 24 перестановки четырех осей, 2⁴= 16 для отражения по каждой оси. Есть 3 небольшие индексные подгруппы, первые две порождают однородные 4-многогранники, которые также повторяются в других семействах [1⁺,4,3,3], [4,(3,3)⁺] и [4,3,3]⁺, всего порядка 192.

Усечения Тессеракта

#	имя	Вершина фигура	Диаграмма Кокстера и Schläfli символы	Подсчет клеток по местоположению					Количество элементов
#	имя	Вершина фигура	Диаграмма Кокстера и Schläfli символы	Поз. 3 (8)	Поз. 2 (24)	Поз. 1 (32)	Поз. 0 (16)	Клетки	Лица	Края	Вершины
10	тессеракт или 8-элементный		{4,3,3}	(4) (4.4.4)				8	24	32	16
11	Исправленный тессеракт		г {4,3,3}	(3) (3.4.3.4)			(2) (3.3.3)	24	88	96	32
13	Усеченный тессеракт		т {4,3,3}	(3) (3.8.8)			(1) (3.3.3)	24	88	128	64
14	Кантеллированный тессеракт		рр {4,3,3}	(1) (3.4.4.4)		(2) (3.4.4)	(1) (3.3.3.3)	56	248	288	96
15	Бегущий тессеракт (также беглый 16-клеточный)		т_0,3{4,3,3}	(1) (4.4.4)	(3) (4.4.4)	(3) (3.4.4)	(1) (3.3.3)	80	208	192	64
16	Обрезанный тессеракт (также усеченный битами 16 ячеек)		2т {4,3,3}	(2) (4.6.6)			(2) (3.6.6)	24	120	192	96
18	Усеченный тессеракт		tr {4,3,3}	(2) (4.6.8)		(1) (3.4.4)	(1) (3.6.6)	56	248	384	192
19	Выполнить усеченный тессеракт		т_0,1,3{4,3,3}	(1) (3.8.8)	(2) (4.4.8)	(1) (3.4.4)	(1) (3.4.3.4)	80	368	480	192
21	Омниусеченный тессеракт (также усеченная 16-ячеечная)		т_0,1,2,3{3,3,4}	(1) (4.6.8)	(1) (4.4.8)	(1) (4.4.6)	(1) (4.6.6)	80	464	768	384

Связанная половина тессеракта, [1⁺, 4,3,3] равномерные 4-многогранники
#	имя	Вершина фигура	Диаграмма Кокстера и Schläfli символы	Подсчет клеток по местоположению					Количество элементов
#	имя	Вершина фигура	Диаграмма Кокстера и Schläfli символы	Поз. 3 (8)	Поз. 2 (24)	Поз. 1 (32)	Поз. 0 (16)	Alt	Клетки	Лица	Края	Вершины
12	Половина тессеракта Demitesseract 16 ячеек		= h {4,3,3} = {3,3,4}	(4) (3.3.3)				(4) (3.3.3)	16	32	24	8
[17]	Кантический тессеракт (Или усеченный 16-элементный )		= час₂{4,3,3} = t {4,3,3}	(4) (6.6.3)			(1) (3.3.3.3)		24	96	120	48
[11]	Рунический тессеракт (Или исправленный тессеракт )		= час₃{4,3,3} = r {4,3,3}	(3) (3.4.3.4)			(2) (3.3.3)		24	88	96	32
[16]	Runcicantic tesseract (Или усеченный битами тессеракт )		= час_2,3{4,3,3} = 2t {4,3,3}	(2) (3.4.3.4)			(2) (3.6.6)		24	120	192	96
[11]	(исправленный тессеракт )		= час₁{4,3,3} = r {4,3,3}						24	88	96	32
[16]	(усеченный битами тессеракт )		= час_1,2{4,3,3} = 2t {4,3,3}						24	120	192	96
[23]	(выпрямленный 24-элементный )		= час_1,3{4,3,3} = rr {3,3,4}						48	240	288	96
[24]	(усеченный 24-элементный )		= час_1,2,3{4,3,3} = tr {3,3,4}						48	240	384	192

#	имя	Вершина фигура	Диаграмма Кокстера и Schläfli символы	Подсчет клеток по местоположению					Количество элементов
#	имя	Вершина фигура	Диаграмма Кокстера и Schläfli символы	Поз. 3 (8)	Поз. 2 (24)	Поз. 1 (32)	Поз. 0 (16)	Alt	Клетки	Лица	Края	Вершины
Неоднородный	омниснуб тессеракт^[15] (Или omnisnub 16 ячеек)		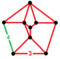ht_0,1,2,3{4,3,3}	(1) (3.3.3.3.4)	(1) (3.3.3.4)	(1) (3.3.3.3)	(1) (3.3.3.3.3)	(4) (3.3.3)	272	944	864	192

16-ячеечные усечения

#	имя	Вершина фигура	Диаграмма Кокстера и Schläfli символы	Подсчет клеток по местоположению					Количество элементов
#	имя	Вершина фигура	Диаграмма Кокстера и Schläfli символы	Поз. 3 (8)	Поз. 2 (24)	Поз. 1 (32)	Поз. 0 (16)	Alt	Клетки	Лица	Края	Вершины
[12]	16 ячеек, гексадекахорон^[7]		{3,3,4}				(8) (3.3.3)		16	32	24	8
[22]	* выпрямленный 16-элементный (Такой же как 24-элементный )		= г {3,3,4}	(2) (3.3.3.3)			(4) (3.3.3.3)		24	96	96	24
17	усеченный 16-элементный		т {3,3,4}	(1) (3.3.3.3)			(4) (3.6.6)		24	96	120	48
[23]	* скошенный 16-элементный (Такой же как выпрямленный 24-элементный )		= рр {3,3,4}	(1) (3.4.3.4)	(2) (4.4.4)		(2) (3.4.3.4)		48	240	288	96
[15]	беглый 16-клеточный (также беглый 8-клеточный)		т_0,3{3,3,4}	(1) (4.4.4)	(3) (4.4.4)	(3) (3.4.4)	(1) (3.3.3)		80	208	192	64
[16]	усеченный битами 16 ячеек (также усеченный битами 8-элементный)		2т {3,3,4}	(2) (4.6.6)			(2) (3.6.6)		24	120	192	96
[24]	* усеченный 16-элементный (Такой же как усеченный 24-элементный )		= tr {3,3,4}	(1) (4.6.6)	(1) (4.4.4)		(2) (4.6.6)		48	240	384	192
20	усеченный 16-элементный		т_0,1,3{3,3,4}	(1) (3.4.4.4)	(1) (4.4.4)	(2) (4.4.6)	(1) (3.6.6)		80	368	480	192
[21]	усеченная 16-ячеечная (также усеченный 8-элементный)		т_0,1,2,3{3,3,4}	(1) (4.6.8)	(1) (4.4.8)	(1) (4.4.6)	(1) (4.6.6)		80	464	768	384
[31]	чередующийся косяк усеченный 16-элементный (То же, что и курносый 24-элементный )		sr {3,3,4}	(1) (3.3.3.3.3)		(1) (3.3.3)	(2) (3.3.3.3.3)	(4) (3.3.3)	144	480	432	96
Неоднородный	Runcic snub rectified 16-элементный		SR₃{3,3,4}	(1) (3.4.4.4)	(2) (3.4.4)	(1) (4.4.4)	(1) (3.3.3.3.3)	(2) (3.4.4)	176	656	672	192

(*) Так же, как исправление тетраэдр производит октаэдр, выпрямляя 16-элементный, получается 24-элементный, обычный член следующего семейства.

В курносый 24-элементный повторяется в этой семье для полноты. Это чередование усеченный 16-элементный или усеченный 24-элементный, с группой полусимметрии [(3,3)⁺, 4]. Усеченные октаэдрические ячейки становятся икосаэдрами. Кубики превращаются в тетраэдры, и 96 новых тетраэдров создаются в промежутках из удаленных вершин.

F₄ семья

В этой семье есть диплоидный икозитетрахорический симметрия,^[7] [3,4,3], из порядок 24 × 48 = 1152: 48 симметрий октаэдра для каждой из 24 ячеек. Есть 3 подгруппы с малым индексом, причем первые две изоморфные пары образуют однородные 4-многогранники, которые также повторяются в других семействах [3⁺,4,3], [3,4,3⁺] и [3,4,3]⁺, всего порядка 576.

[3,4,3] равномерные 4-многогранники
#	имя	Вершина фигура	Диаграмма Кокстера и Schläfli символы	Подсчет клеток по местоположению				Количество элементов
#	имя	Вершина фигура	Диаграмма Кокстера и Schläfli символы	Поз. 3 (24)	Поз. 2 (96)	Поз. 1 (96)	Поз. 0 (24)	Клетки	Лица	Края	Вершины
22	24-элементный, икоситетрахорон^[7] (Такой же как выпрямленный 16-элементный)		{3,4,3}	(6) (3.3.3.3)				24	96	96	24
23	выпрямленный 24-элементный (Такой же как скошенный 16-элементный)		г {3,4,3}	(3) (3.4.3.4)			(2) (4.4.4)	48	240	288	96
24	усеченный 24-элементный (Такой же как усеченный 16-элементный)		т {3,4,3}	(3) (4.6.6)			(1) (4.4.4)	48	240	384	192
25	наклонный 24-элементный		рр {3,4,3}	(2) (3.4.4.4)		(2) (3.4.4)	(1) (3.4.3.4)	144	720	864	288
28	усеченный 24-элементный		tr {3,4,3}	(2) (4.6.8)		(1) (3.4.4)	(1) (3.8.8)	144	720	1152	576
29	усеченный 24-элементный		т_0,1,3{3,4,3}	(1) (4.6.6)	(2) (4.4.6)	(1) (3.4.4)	(1) (3.4.4.4)	240	1104	1440	576

[3⁺, 4,3] равномерные 4-многогранники
#	имя	Вершина фигура	Диаграмма Кокстера и Schläfli символы	Подсчет клеток по местоположению					Количество элементов
#	имя	Вершина фигура	Диаграмма Кокстера и Schläfli символы	Поз. 3 (24)	Поз. 2 (96)	Поз. 1 (96)	Поз. 0 (24)	Alt	Клетки	Лица	Края	Вершины
31	†курносый 24-элементный		с {3,4,3}	(3) (3.3.3.3.3)			(1) (3.3.3)	(4) (3.3.3)	144	480	432	96
Неоднородный	runcic snub 24-элементный		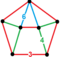s₃{3,4,3}	(1) (3.3.3.3.3)	(2) (3.4.4)		(1) (3.6.6)	(3) Трикап	240	960	1008	288
[25]	кантик курносый 24-элементный (Такой же как наклонный 24-элементный )		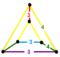s₂{3,4,3}	(2) (3.4.4.4)			(1) (3.4.3.4)	(2) (3.4.4)	144	720	864	288
[29]	рунический курносый 24-элементный (Такой же как усеченный 24-элементный )		s_2,3{3,4,3}	(1) (4.6.6)		(1) (3.4.4)	(1) (3.4.4.4)	(2) (4.4.6)	240	1104	1440	576

(†) Курносый 24-элементный здесь, несмотря на свое общее название, не является аналогом курносый куб; скорее, выводится чередование усеченной 24-клеточной. это число симметрии всего 576, ( ионный уменьшенный икозитетрахорический группа, [3⁺,4,3]).

Как и 5-элементный, 24-элементный самодвойственный, поэтому следующие три формы имеют в два раза больше симметрий, в результате чего их общее количество составляет 2304 (расширенная икозитетрахорическая симметрия [[3,4,3]]).

[[3,4,3]] равномерные 4-многогранники
#	имя	Вершина фигура	Диаграмма Кокстера и Schläfli символы	Подсчет клеток по местоположению			Количество элементов
#	имя	Вершина фигура	Диаграмма Кокстера и Schläfli символы	Поз. 3-0 (48)	Поз. 2-1 (192)	Клетки	Лица	Края	Вершины
26	беглый 24-элементный		т_0,3{3,4,3}	(2) (3.3.3.3)	(6) (3.4.4)	240	672	576	144
27	усеченный битами 24 ячейки тетраконтоктахорон		2т {3,4,3}	(4) (3.8.8)		48	336	576	288
30	комплексно усеченные 24 ячейки		т_0,1,2,3{3,4,3}	(2) (4.6.8)	(2) (4.4.6)	240	1392	2304	1152

[[3,4,3]]⁺ изогональный 4-многогранник
#	имя	Вершина фигура	Диаграмма Кокстера и Schläfli символы	Подсчет клеток по местоположению			Количество элементов
#	имя	Вершина фигура	Диаграмма Кокстера и Schläfli символы	Поз. 3-0 (48)	Поз. 2-1 (192)	Alt	Клетки	Лица	Края	Вершины
Неоднородный	omnisnub 24 ячейки^[16]		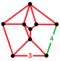ht_0,1,2,3{3,4,3}	(2) (3.3.3.3.4)	(2) (3.3.3.3)	(4) (3.3.3)	816	2832	2592	576

H₄ семья

В этой семье есть диплоидный гексакозихорический симметрия,^[7] [5,3,3], из порядок 120 × 120 = 24 × 600 = 14400: 120 для каждого из 120 додекаэдров или 24 для каждого из 600 тетраэдров. Есть одна небольшая индексная подгруппа [5,3,3]⁺, всего порядка 7200.

Усечения на 120 ячеек

#	имя	Вершина фигура	Диаграмма Кокстера и Schläfli символы	Подсчет клеток по местоположению					Количество элементов
#	имя	Вершина фигура	Диаграмма Кокстера и Schläfli символы	Поз. 3 (120)	Поз. 2 (720)	Поз. 1 (1200)	Поз. 0 (600)	Alt	Клетки	Лица	Края	Вершины
32	120 ячеек (гекатоникосахорон или додекаконтахорон)^[7]		{5,3,3}	(4) (5.5.5)					120	720	1200	600
33	выпрямленный 120-элементный		г {5,3,3}	(3) (3.5.3.5)			(2) (3.3.3)		720	3120	3600	1200
36	усеченный 120-элементный		т {5,3,3}	(3) (3.10.10)			(1) (3.3.3)		720	3120	4800	2400
37	скошенный 120-элементный		рр {5,3,3}	(1) (3.4.5.4)		(2) (3.4.4)	(1) (3.3.3.3)		1920	9120	10800	3600
38	беглый 120-клеточный (также беглый 600-клеточный)		т_0,3{5,3,3}	(1) (5.5.5)	(3) (4.4.5)	(3) (3.4.4)	(1) (3.3.3)		2640	7440	7200	2400
39	усеченный по битам 120-элементный (также усеченный битами, 600 ячеек)		2т {5,3,3}	(2) (5.6.6)			(2) (3.6.6)		720	4320	7200	3600
42	усеченный 120-элементный		tr {5,3,3}	(2) (4.6.10)		(1) (3.4.4)	(1) (3.6.6)		1920	9120	14400	7200
43	усеченный 120-элементный		т_0,1,3{5,3,3}	(1) (3.10.10)	(2) (4.4.10)	(1) (3.4.4)	(1) (3.4.3.4)		2640	13440	18000	7200
46	усеченная 120-ячеечная (также усеченный 600-ячеечный)		т_0,1,2,3{5,3,3}	(1) (4.6.10)	(1) (4.4.10)	(1) (4.4.6)	(1) (4.6.6)		2640	17040	28800	14400
Неоднородный	omnisnub 120 ячеек^[17] (То же, что и омниснуб на 600 ячеек)		ht_0,1,2,3{5,3,3}	(1) (3.3.3.3.5)	(1) (3.3.3.5)	(1) (3.3.3.3)	(1) (3.3.3.3.3)	(4) (3.3.3)	9840	35040	32400	7200

Усечения на 600 ячеек

#	имя	Вершина фигура	Диаграмма Кокстера и Schläfli символы	Симметрия	Подсчет клеток по местоположению				Количество элементов
#	имя	Вершина фигура	Диаграмма Кокстера и Schläfli символы	Симметрия	Поз. 3 (120)	Поз. 2 (720)	Поз. 1 (1200)	Поз. 0 (600)	Клетки	Лица	Края	Вершины
35	600 ячеек, гексакосихорон^[7]		{3,3,5}	[5,3,3] заказ 14400				(20) (3.3.3)	600	1200	720	120
[47]	20-элементный 600-элементный (великая антипризма )		Nonwythoffian строительство	[[10,2⁺,10]] порядка 400 Указатель 36	(2) (3.3.3.5)			(12) (3.3.3)	320	720	500	100
[31]	24 уменьшенных 600-ячеек (курносый 24-элементный )		Nonwythoffian строительство	[3⁺,4,3] заказ 576 индекс 25	(3) (3.3.3.3.3)			(5) (3.3.3)	144	480	432	96
Неоднородный	bi-24-уменьшенный 600-ячеечный		Nonwythoffian строительство	заказ 144 индекс 100	(6) tdi				48	192	216	72
34	выпрямленный 600-элементный		г {3,3,5}	[5,3,3]	(2) (3.3.3.3.3)			(5) (3.3.3.3)	720	3600	3600	720
Неоднородный	120-элементный выпрямленный 600-элементный		Nonwythoffian строительство	заказ 1200 индекс 12	(2) 3.3.3.5	(2) 4.4.5		(5) P4	840	2640	2400	600
41	усеченный 600-ячеечный		т {3,3,5}	[5,3,3]	(1) (3.3.3.3.3)			(5) (3.6.6)	720	3600	4320	1440
40	скошенный 600-ячеечный		рр {3,3,5}	[5,3,3]	(1) (3.5.3.5)	(2) (4.4.5)		(1) (3.4.3.4)	1440	8640	10800	3600
[38]	беглый 600-клеточный (также беглый 120-клеточный)		т_0,3{3,3,5}	[5,3,3]	(1) (5.5.5)	(3) (4.4.5)	(3) (3.4.4)	(1) (3.3.3)	2640	7440	7200	2400
[39]	усеченный битами, 600 ячеек (также усеченный по битам 120-элементный)		2т {3,3,5}	[5,3,3]	(2) (5.6.6)			(2) (3.6.6)	720	4320	7200	3600
45	усеченный 600-ячеечный		tr {3,3,5}	[5,3,3]	(1) (5.6.6)	(1) (4.4.5)		(2) (4.6.6)	1440	8640	14400	7200
44	усеченный 600-ячеечный		т_0,1,3{3,3,5}	[5,3,3]	(1) (3.4.5.4)	(1) (4.4.5)	(2) (4.4.6)	(1) (3.6.6)	2640	13440	18000	7200
[46]	усеченный 600-ячеечный (также усеченная 120-ячеечная)		т_0,1,2,3{3,3,5}	[5,3,3]	(1) (4.6.10)	(1) (4.4.10)	(1) (4.4.6)	(1) (4.6.6)	2640	17040	28800	14400

D₄ семья

Эта семья Демитессеракт, [3^1,1,1], не вводит новых равномерных 4-многогранников, но эти альтернативные конструкции стоит повторить. В этой семье есть порядок 12 × 16 = 192: 4! / 2 = 12 перестановок четырех осей, половина как чередующаяся, 2⁴= 16 для отражения по каждой оси. Есть одна небольшая индексная подгруппа, порождающая равномерные 4-многогранники, [3^1,1,1]⁺, заказ 96.

[3^1,1,1] равномерные 4-многогранники
#	имя	Вершина фигура	Диаграмма Кокстера = =	Подсчет клеток по местоположению					Количество элементов
#	имя	Вершина фигура	Диаграмма Кокстера = =	Поз. 0 (8)	Поз. 2 (24)	Поз. 1 (8)	Поз. 3 (8)	Поз. Alt (96)	3	2	1	0
[12]	demitesseract половина тессеракта (Такой же как 16 ячеек )		= ч {4,3,3}			(4) (3.3.3)	(4) (3.3.3)		16	32	24	8
[17]	кантик тессеракт (Такой же как усеченный 16-элементный )		= час₂{4,3,3}	(1) (3.3.3.3)		(2) (3.6.6)	(2) (3.6.6)		24	96	120	48
[11]	рунический тессеракт (Такой же как исправленный тессеракт )		= час₃{4,3,3}	(1) (3.3.3)		(1) (3.3.3)	(3) (3.4.3.4)		24	88	96	32
[16]	рунический тессеракт (Такой же как усеченный битами тессеракт )		= час_2,3{4,3,3}	(1) (3.6.6)		(1) (3.6.6)	(2) (4.6.6)		24	96	96	24

Когда 3 раздвоенных узла ветвления одинаково окружены кольцами, симметрия может быть увеличена на 6, как [3 [3^1,1,1]] = [3,4,3], поэтому эти многогранники повторяются из 24-элементный семья.

[3[3^1,1,1]] равномерные 4-многогранники
#	имя	Вершина фигура	Диаграмма Кокстера = =	Подсчет клеток по местоположению			Количество элементов
#	имя	Вершина фигура	Диаграмма Кокстера = =	Поз. 0,1,3 (24)	Поз. 2 (24)	Поз. Alt (96)	3	2	1	0
[22]	выпрямленный 16-элементный) (Такой же как 24-элементный )		= = = {3^1,1,1} = г {3,3,4} = {3,4,3}	(6) (3.3.3.3)			48	240	288	96
[23]	скошенный 16-элементный (Такой же как выпрямленный 24-элементный )		= = = г {3^1,1,1} = rr {3,3,4} = r {3,4,3}	(3) (3.4.3.4)	(2) (4.4.4)		24	120	192	96
[24]	усеченный 16-элементный (Такой же как усеченный 24-элементный )		= = = т {3^1,1,1} = tr {3,3,4} = t {3,4,3}	(3) (4.6.6)	(1) (4.4.4)		48	240	384	192
[31]	курносый 24-элементный		= = = с {3^1,1,1} = sr {3,3,4} = s {3,4,3}	(3) (3.3.3.3.3)	(1) (3.3.3)	(4) (3.3.3)	144	480	432	96

Здесь снова курносый 24-элементный, с группой симметрии [3^1,1,1]⁺ на этот раз представляет собой чередующееся усечение усеченных 24-ячеек, создающее 96 новых тетраэдров в позиции удаленных вершин. В отличие от его появления внутри прежних групп как частично курносый 4-многогранник, только внутри этой группы симметрии он имеет полную аналогию с курносыми Кеплера, т.е. курносый куб и курносый додекаэдр.

Великая антипризма

Существует один невыпуклый 4-мерный многогранник, не являющийся Витофовым, известный как великая антипризма, состоящий из 20 пятиугольные антипризмы образуя два перпендикулярных кольца, соединенных 300 тетраэдры. Это примерно аналог трехмерного антипризмы, состоящие из двух параллельных полигоны присоединился к группе треугольники. Однако, в отличие от них, большая антипризма не является членом бесконечного семейства однородных многогранников.

Его симметрия - это ионная уменьшенная группа Кокстера, [[10,2⁺, 10]], заказ 400.

#	имя	Картина	Вершина фигура	Диаграмма Кокстера и Schläfli символы	Ячейки по типу		Количество элементов				Сеть
#	имя	Картина	Вершина фигура	Диаграмма Кокстера и Schläfli символы	Ячейки по типу		Клетки	Лица	Края	Вершины	Сеть
47	великая антипризма			Нет символа	300 (3.3.3 )	20 (3.3.3.5 )	320	20 {5} 700 {3}	500	100

Призматические однородные 4-многогранники

Призматический многогранник - это Декартово произведение двух многогранников меньшей размерности; знакомыми примерами являются трехмерные призмы, которые являются продуктами многоугольник и отрезок. Призматические равномерные 4-многогранники состоят из двух бесконечных семейств:

Многогранные призмы: произведения отрезка прямой и равномерный многогранник. Это семейство бесконечно, потому что оно включает призмы, построенные на трехмерных призмах, и антипризмы.
Дуопризма: произведение двух многоугольников.

Выпуклые многогранные призмы

Наиболее очевидное семейство призматических 4-многогранников - это многогранные призмы, т.е. произведения многогранника с отрезок. Клетки такого 4-многогранника представляют собой два одинаковых однородных многогранника, лежащих параллельно гиперплоскости (в база ячеек) и соединяющий их слой призм ( боковой ячеек). В это семейство входят призмы для 75 непризматических равномерные многогранники (из них 18 выпуклых; одна из них, кубическая призма, указана выше как тессеракт).^{[нужна цитата ]}

Есть 18 выпуклых многогранных призм создано из 5 Платоновы тела и 13 Архимедовы тела а также для бесконечных семейств трехмерных призмы и антипризмы.^{[нужна цитата ]} Число симметрии многогранной призмы вдвое больше, чем у базового многогранника.

Тетраэдрические призмы: A₃ × А₁

Эта призматическая тетраэдрическая симметрия равно [3,3,2], порядок 48. Есть две подгруппы индекса 2, [(3,3)⁺, 2] и [3,3,2]⁺, но второй не порождает равномерный 4-многогранник.

[3,3,2] равномерные 4-многогранники
#	имя	Картина	Вершина фигура	Диаграмма Кокстера и Schläfli символы	Ячейки по типу			Количество элементов				Сеть
#	имя	Картина	Вершина фигура	Диаграмма Кокстера и Schläfli символы	Ячейки по типу			Клетки	Лица	Края	Вершины	Сеть
48	Тетраэдрическая призма			{3,3}×{ } т_0,3{3,3,2}	2 3.3.3	4 3.4.4		6	8 {3} 6 {4}	16	8
49	Усеченная тетраэдрическая призма			т {3,3} × {} т_0,1,3{3,3,2}	2 3.6.6	4 3.4.4	4 4.4.6	10	8 {3} 18 {4} 8 {6}	48	24

[[3,3], 2] равномерные 4-многогранники
#	имя	Картина	Вершина фигура	Диаграмма Кокстера и Schläfli символы	Ячейки по типу			Количество элементов				Сеть
#	имя	Картина	Вершина фигура	Диаграмма Кокстера и Schläfli символы	Ячейки по типу			Клетки	Лица	Края	Вершины	Сеть
[51]	Выпрямленная тетраэдрическая призма (Такой же как восьмигранная призма )			г {3,3} × {} т_1,3{3,3,2}	2 3.3.3.3	4 3.4.4		6	16 {3} 12 {4}	30	12
[50]	Скошенная тетраэдрическая призма (Такой же как кубооктаэдрическая призма )			rr {3,3} × {} т_0,2,3{3,3,2}	2 3.4.3.4	8 3.4.4	6 4.4.4	16	16 {3} 36 {4}	60	24
[54]	Углово-усеченная тетраэдрическая призма (Такой же как усеченная восьмигранная призма )			tr {3,3} × {} т_0,1,2,3{3,3,2}	2 4.6.6	8 6.4.4	6 4.4.4	16	48 {4} 16 {6}	96	48
[59]	Плоская четырехгранная призма (Такой же как икосаэдрическая призма )			sr {3,3} × {}	2 3.3.3.3.3	20 3.4.4		22	40 {3} 30 {4}	72	24
Неоднородный	всенаправленная тетраэдрическая антипризма			${ displaystyle s left {{ begin {array} {l} 3 3 2 end {array}} right }}$	2 3.3.3.3.3	8 3.3.3.3	6+24 3.3.3	40	16+96 {3}	96	24

Октаэдрические призмы: B₃ × А₁

Эта призматическая восьмигранная симметрия семейства это [4,3,2], порядок 96. Есть 6 подгрупп индекса 2 порядка 48, которые ниже выражены в чередующихся 4-многогранниках. Симметрии являются [(4,3)⁺,2], [1⁺,4,3,2], [4,3,2⁺], [4,3⁺,2], [4,(3,2)⁺] и [4,3,2]⁺.

#	имя	Картина	Вершина фигура	Диаграмма Кокстера и Schläfli символы	Ячейки по типу				Количество элементов				Сеть
#	имя	Картина	Вершина фигура	Диаграмма Кокстера и Schläfli символы	Ячейки по типу				Клетки	Лица	Края	Вершины	Сеть
[10]	Кубическая призма (Такой же как тессеракт ) (Такой же как 4-4 дуопризма)			{4,3}×{ } т_0,3{4,3,2}	2 4.4.4	6 4.4.4			8	24 {4}	32	16
50	Кубооктаэдрическая призма (Такой же как наклонная четырехгранная призма)			г {4,3} × {} т_1,3{4,3,2}	2 3.4.3.4	8 3.4.4	6 4.4.4		16	16 {3} 36 {4}	60	24
51	Октаэдрическая призма (Такой же как выпрямленная тетраэдрическая призма) (Такой же как треугольная антипризматическая призма)			{3,4}×{ } т_2,3{4,3,2}	2 3.3.3.3	8 3.4.4			10	16 {3} 12 {4}	30	12
52	Ромбокубооктаэдрическая призма			rr {4,3} × {} т_0,2,3{4,3,2}	2 3.4.4.4	8 3.4.4	18 4.4.4		28	16 {3} 84 {4}	120	48
53	Усеченная кубическая призма			т {4,3} × {} т_0,1,3{4,3,2}	2 3.8.8	8 3.4.4	6 4.4.8		16	16 {3} 36 {4} 12 {8}	96	48
54	Усеченная восьмигранная призма (Такой же как усеченная четырехгранная призма)			т {3,4} × {} т_1,2,3{4,3,2}	2 4.6.6	6 4.4.4	8 4.4.6		16	48 {4} 16 {6}	96	48
55	Усеченная кубооктаэдрическая призма			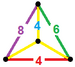tr {4,3} × {} т_0,1,2,3{4,3,2}	2 4.6.8	12 4.4.4	8 4.4.6	6 4.4.8	28	96 {4} 16 {6} 12 {8}	192	96
56	Плоская кубическая призма		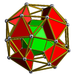	sr {4,3} × {}	2 3.3.3.3.4	32 3.4.4	6 4.4.4		40	64 {3} 72 {4}	144	48
[48]	Тетраэдрическая призма			h {4,3} × {}	2 3.3.3	4 3.4.4			6	8 {3} 6 {4}	16	8
[49]	Усеченная тетраэдрическая призма			час₂{4,3}×{ }	2 3.3.6	4 3.4.4	4 4.4.6		6	8 {3} 6 {4}	16	8
[50]	Кубооктаэдрическая призма			rr {3,3} × {}	2 3.4.3.4	8 3.4.4	6 4.4.4		16	16 {3} 36 {4}	60	24
[52]	Ромбокубооктаэдрическая призма			s₂{3,4}×{ }	2 3.4.4.4	8 3.4.4	18 4.4.4		28	16 {3} 84 {4}	120	48
[54]	Усеченная восьмигранная призма			tr {3,3} × {}	2 4.6.6	6 4.4.4	8 4.4.6		16	48 {4} 16 {6}	96	48
[59]	Икосаэдрическая призма			с {3,4} × {}	2 3.3.3.3.3	20 3.4.4			22	40 {3} 30 {4}	72	24
[12]	16 ячеек		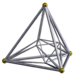	с {2,4,3}	2+6+8 3.3.3.3				16	32 {3}	24	8
Неоднородный	Омниснуб тетраэдрическая антипризма			sr {2,3,4}	2 3.3.3.3.3	8 3.3.3.3	6+24 3.3.3		40	16+96 {3}	96	24
Неоднородный	Омниснуб кубическая антипризма			${ displaystyle s left {{ begin {array} {l} 4 3 2 end {array}} right }}$	2 3.3.3.3.4	12+48 3.3.3	8 3.3.3.3	6 3.3.3.4	76	16+192 {3} 12 {4}	192	48
Неоднородный	Рунический курносый кубический хосохорон			s₃{2,4,3}	2 3.6.6	6 3.3.3	8 треугольный купол		16	52	60	24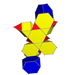

Икосаэдрические призмы: H₃ × А₁

Эта призматическая икосаэдрическая симметрия равно [5,3,2], порядок 240. Есть две подгруппы индекса 2, [(5,3)⁺, 2] и [5,3,2]⁺, но второй не создает однородного полихорона.

#	имя	Картина	Вершина фигура	Диаграмма Кокстера и Schläfli символы	Ячейки по типу				Количество элементов				Сеть
#	имя	Картина	Вершина фигура	Диаграмма Кокстера и Schläfli символы	Ячейки по типу				Клетки	Лица	Края	Вершины	Сеть
57	Додекаэдрическая призма			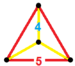{5,3}×{ } т_0,3{5,3,2}	2 5.5.5	12 4.4.5			14	30 {4} 24 {5}	80	40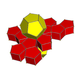
58	Икозододекаэдрическая призма		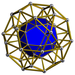	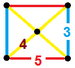г {5,3} × {} т_1,3{5,3,2}	2 3.5.3.5	20 3.4.4	12 4.4.5		34	40 {3} 60 {4} 24 {5}	150	60
59	Икосаэдрическая призма (такой же как плоскостная тетраэдрическая призма)			{3,5}×{ } т_2,3{5,3,2}	2 3.3.3.3.3	20 3.4.4			22	40 {3} 30 {4}	72	24
60	Усеченная додекаэдрическая призма		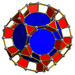	т {5,3} × {} т_0,1,3{5,3,2}	2 3.10.10	20 3.4.4	12 4.4.10		34	40 {3} 90 {4} 24 {10}	240	120
61	Ромбикосододекаэдрическая призма			rr {5,3} × {} т_0,2,3{5,3,2}	2 3.4.5.4	20 3.4.4	30 4.4.4	12 4.4.5	64	40 {3} 180 {4} 24 {5}	300	120
62	Усеченная икосаэдрическая призма			т {3,5} × {} т_1,2,3{5,3,2}	2 5.6.6	12 4.4.5	20 4.4.6		34	90 {4} 24 {5} 40 {6}	240	120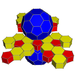
63	Усеченная икосододекаэдрическая призма		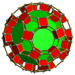	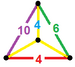tr {5,3} × {} т_0,1,2,3{5,3,2}	2 4.6.10	30 4.4.4	20 4.4.6	12 4.4.10	64	240 {4} 40 {6} 24 {10}	480	240
64	Плоская додекаэдрическая призма			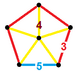sr {5,3} × {}	2 3.3.3.3.5	80 3.4.4	12 4.4.5		94	160 {3} 150 {4} 24 {5}	360	120
Неоднородный	Омниснуб додекаэдрическая антипризма			${ displaystyle s left {{ begin {array} {l} 5 3 2 end {array}} right }}$	2 3.3.3.3.5	30+120 3.3.3	20 3.3.3.3	12 3.3.3.5	184	20+240 {3} 24 {5}	220	120

Дуопризмы: [p] × [q]

Самая простая из дуопризм - 3,3-дуопризма в Диаграмма Шлегеля, один из 6 треугольная призма показаны ячейки.

Второй - бесконечная семья однородные дуопризмы, изделия двух правильные многоугольники. Дуопризма Диаграмма Кокстера-Дынкина является . это вершина фигуры это дисфеноидный тетраэдр, .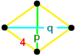

Это семейство частично совпадает с первым: когда один из двух «факторных» многоугольников является квадратом, продукт эквивалентен гиперпризме, основание которой представляет собой трехмерную призму. Число симметрии дуопризмы, факторы которой равны п-угольник и q-гон (а "р, д-duoprism ») равно 4pq если п≠q; если оба фактора п-угольников, число симметрии 8п². Тессеракт также можно считать 4,4-дуопризмой.

Элементы р, д-дуопризма (п ≥ 3, q ≥ 3) являются:

Ячейки: п q-угольные призмы, q п-угольные призмы
Лица: pq квадраты п q-угольники, q п-угольники
Края: 2pq
Вершины: pq

Нет единого аналога в четырех измерениях бесконечному семейству трехмерных антипризмы.

Бесконечный набор p-q дуопризма - - п q-угольные призмы, q п-угольные призмы:

имя	Граф Кокстера	Клетки	Картинки	Сеть
3-3 дуопризма		3 + 3 треугольные призмы
3-4 дуопризма		3 кубика 4 треугольные призмы
4-4 дуопризма (так же, как тессеракт)		4 + 4 кубика
3-5 дуопризма		3 пятиугольные призмы 5 треугольных призм
4-5 дуопризма		4 пятиугольные призмы 5 кубиков
5-5 дуопризма		5 + 5 пятиугольных призм
3-6 дуопризма		3 шестигранные призмы 6 треугольных призм
4-6 дуопризма		4 шестиугольные призмы 6 кубиков
5-6 дуопризма		5 шестиугольных призм 6 пятиугольных призм
6-6 дуопризма		6 + 6 шестиугольных призм

3-3	3-4	3-5	3-6	3-7	3-8
4-3	4-4	4-5	4-6	4-7	4-8
5-3	5-4	5-5	5-6	5-7	5-8
6-3	6-4	6-5	6-6	6-7	6-8
7-3	7-4	7-5	7-6	7-7	7-8
8-3	8-4	8-5	8-6	8-7	8-8

Многоугольные призмы: [p] × [] × []

Бесконечный набор однородных призматических призм перекрывается с 4-p дуопризмами: (p≥3) - - п кубики и 4 п-гональные призмы - (Все такие же, как 4-п дуопризма) Второй многогранник в серии является нижней симметрией правильного тессеракт, {4}×{4}.

Выпуклый п-угольные призматические призмы
имя	{3}×{4}	{4}×{4}	{5}×{4}	{6}×{4}	{7}×{4}	{8}×{4}	{p} × {4}
Coxeter диаграммы
Образ
Клетки	3 {4}×{} 4 {3}×{}	4 {4}×{} 4 {4}×{}	5 {4}×{} 4 {5}×{}	6 {4}×{} 4 {6}×{}	7 {4}×{} 4 {7}×{}	8 {4}×{} 4 {8}×{}	п {4}×{} 4 {p} × {}
Сеть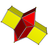

Многоугольные антипризматические призмы: [p] × [] × []

Бесконечные множества однородные антипризматические призмы построены из двух параллельных однородных антипризмы ): (p≥2) - - 2 п-гональные антипризмы, соединенные 2 п-угольные призмы и 2p треугольные призмы.

Выпуклый п-угольные антипризматические призмы
имя	с {2,2} × {}	с {2,3} × {}	с {2,4} × {}	с {2,5} × {}	с {2,6} × {}	с {2,7} × {}	с {2,8} × {}	s {2, p} × {}
Coxeter диаграмма
Образ
Вершина фигура
Клетки	2 с {2,2} (2) {2}×{}={4} 4 {3}×{}	2 с {2,3} 2 {3}×{} 6 {3}×{}	2 с {2,4} 2 {4}×{} 8 {3}×{}	2 с {2,5} 2 {5}×{} 10 {3}×{}	2 с {2,6} 2 {6}×{} 12 {3}×{}	2 с {2,7} 2 {7}×{} 14 {3}×{}	2 с {2,8} 2 {8}×{} 16 {3}×{}	2 с {2, p} 2 {p} × {} 2п {3}×{}
Сеть

А p-угольная антипризматическая призма имеет 4p треугольник, 4p квадрат и 4 р-угольники лица. Она имеет 10p края и 4p вершины.

Неравномерные чередования

Как трехмерный курносый куб,

, чередование удаляет половину вершин в двух киральных наборах вершин из окольцованной формы

, Однако униформа Решение требует, чтобы положения вершин были отрегулированы на одинаковую длину. В четырех измерениях эта корректировка возможна только для 2 чередующихся фигур, в то время как остальные существуют только как неравносторонние чередующиеся фигуры.

Кокстер показал только два равномерных решения для групп Кокстера ранга 4 со всеми кольцами чередовались (показан с пустыми узлами круга). Первый , с {2^1,1,1}, которая представляла подгруппу индекса 24 (симметрия [2,2,2]⁺, порядок 8) форма demitesseract, , h {4,3,3} (симметрия [1⁺,4,3,3] = [3^1,1,1], заказ 192). Второй , с {3^1,1,1}, которая является подгруппой индекса 6 (симметрия [3^1,1,1]⁺, приказ 96) форма курносый 24-элементный, , s {3,4,3}, (симметрия [3⁺, 4,3], заказ 576).

Другие варианты, такие как , как альтернатива полностью усеченный тессеракт , нельзя сделать однородным, так как решение для равных длин кромок в общем случае сверхопределенный (есть шесть уравнений, но только четыре переменные). Такие неравномерные чередующиеся фигуры можно построить как вершинно-транзитивный 4-многогранники путем удаления одного из двух полумножеств вершин полностью окольцованной фигуры, но будут иметь неравные длины ребер. Как и равномерные чередования, они будут иметь половину симметрии однородной фигуры, как [4,3,3]⁺порядка 192 - симметрия альтернативный полностью усеченный тессеракт.^[18]

Конструкции Wythoff с чередованием производят вершинно-транзитивный фигуры, которые можно сделать равносторонними, но не однородными, потому что чередующиеся промежутки (вокруг удаленных вершин) создают ячейки, которые не являются правильными или полурегулярными. Предлагаемое название таких фигурок: чешуйчатые многогранники.^[19] Эта категория допускает подмножество Твердые тела Джонсона как клетки, например треугольный купол.

Каждый конфигурация вершины внутри тела Джонсона должно существовать в пределах вершины фигуры. Например, квадратная детская коляска имеет две конфигурации вершин: 3.3.4 вокруг основания и 3.3.3.3 на вершине.

Сети и фигуры вершин двух выпуклых случаев приведены ниже вместе со списком ячеек вокруг каждой вершины.

Два выпуклых вершинно-транзитивных 4-многогранника с неоднородными ячейками
Coxeter диаграмма	s₃{2,4,3},	s₃{3,4,3},
Связь	24 из 48 вершин ромбокубооктаэдрическая призма	288 из 576 вершин усеченный 24-элементный
Сеть	рунчий курносый кубический хосохорон^[20]^[21]	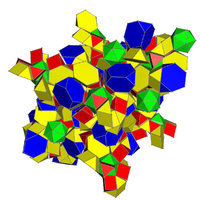runcic snub 24-элементный^[22]^[23]
Клетки
Вершина фигура	(1) 3.4.3.4: треугольный купол (2) 3.4.6: треугольный купол (1) 3.3.3: тетраэдр (1) 3.6.6: усеченный тетраэдр	(1) 3.4.3.4: треугольный купол (2) 3.4.6: треугольный купол (2) 3.4.4: треугольная призма (1) 3.6.6: усеченный тетраэдр (1) 3.3.3.3.3: икосаэдр

Геометрические выводы для 46 непризматических однородных полихор Витоффа

46 4-многогранников Витоффа включают шесть выпуклые правильные 4-многогранники. Остальные сорок могут быть получены из регулярной полихоры с помощью геометрических операций, которые сохраняют большую часть или все их симметрии, и поэтому может быть классифицирован группы симметрии что у них общего.

Сводная диаграмма операций усечения	Пример расположения точки калейдоскопического генератора в фундаментальной области.

Геометрические операции, которые выводят 40 однородных 4-многогранников из правильных 4-многогранников: усечение операции. 4-многогранник может быть усечен по вершинам, ребрам или граням, что приведет к добавлению ячеек, соответствующих этим элементам, как показано в столбцах таблиц ниже.

В Диаграмма Кокстера-Дынкина показывает четыре зеркала калейдоскопа Витоффа как узлы, а края между узлами помечены целым числом, показывающим угол между зеркалами (π /п радианы или 180 /п градусов). Узлы в кружках показывают, какие зеркала активны для каждой формы; зеркало активно по отношению к вершине, которая на нем не лежит.

Операция	Символ Шлефли	Симметрия	Описание
Родитель	т₀{p, q, r}	[p, q, r]	Исходная правильная форма {p, q, r}
Исправление	т₁{p, q, r}		Операция усечения применяется до тех пор, пока исходные ребра не превратятся в точки.
Биректификация (Выпрямленный двойной)	т₂{p, q, r}		Лица полностью усечены до точек. То же, что и выпрямленный двойной.
Триректификация (двойной )	т₃{p, q, r}		Ячейки обрезаются до точек. Правильный двойственный {r, q, p}
Усечение	т_0,1{p, q, r}		Каждая вершина обрезается так, чтобы осталась середина каждого исходного ребра. На месте вершины появляется новая ячейка, родительская вершина фигуры. Каждая исходная ячейка также усекается.
Bitruncation	т_1,2{p, q, r}		Усечение между исправленной формой и двойной исправленной формой.
Усечение	т_2,3{p, q, r}		Усеченный двойственный {r, q, p}.
Cantellation	т_0,2{p, q, r}		Усечение, применяемое к ребрам и вершинам, определяет переход между регулярной и двойственно исправленной формой.
Бикантелляция	т_1,3{p, q, r}		Сквозной двойственный {r, q, p}.
Runcination (или расширение )	т_0,3{p, q, r}		Усечение, примененное к ячейкам, граням и краям; определяет прогрессию между обычной формой и дуальной.
Cantitruncation	т_0,1,2{p, q, r}		Оба песня и усечение операции применяются вместе.
Двухслойное усечение	т_1,2,3{p, q, r}		Урезанный двойственный {r, q, p}.
Runcitruncation	т_0,1,3{p, q, r}		Оба бегство и усечение операции применяются вместе.
Runcicantellation	т_0,1,3{p, q, r}		Выполните усеченный двойственный {r, q, p}.
Омнитуркация (runcicantitruncation)	т_0,1,2,3{p, q, r}		Применение всех трех операторов.
Половина	h {2p, 3, q}	[1⁺, 2p, 3, q] = [(3, p, 3), q]	Чередование из , такой же как
Кантик	час₂{2p, 3, q}		Такой же как
Runcic	час₃{2p, 3, q}		Такой же как
Runcicantic	час_2,3{2p, 3, q}		Такой же как
Квартал	q {2p, 3,2q}	[1⁺, 2п, 3,2кв, 1⁺]	Такой же как
Курносый	s {p, 2q, r}	[п⁺, 2q, r]	Альтернативное усечение
Кантичное пренебрежение	s₂{p, 2q, r}		Кантеллированное попеременное усечение
Рунчик пренебрежительно	s₃{p, 2q, r}		Бугристое попеременное усечение
Runcicantic пренебрежение	s_2,3{p, 2q, r}		Рунцикантеллированное попеременное усечение
Курносый исправленный	sr {p, q, 2r}	[(p, q)⁺, 2р]	Переменное усеченное выпрямление
	ht_0,3{2p, q, 2r}	[(2п, q, 2р, 2⁺)]	Чередование бега
Биснуб	2s {2p, q, 2r}	[2p, q⁺, 2р]	Альтернативное усечение битов
Омниснуб	ht_0,1,2,3{p, q, r}	[p, q, r]⁺	Альтернативное омнитусечение

Смотрите также выпуклые однородные соты, некоторые из которых иллюстрируют эти операции применительно к обычным кубические соты.

Если два многогранника двойники друг друга (например, тессеракт и 16 ячеек или 120 ячеек и 600 ячеек), то усечение битов, бегающий или усекающий либо одна и та же операция производит ту же цифру, что и другая. Таким образом, если в таблице фигурирует только причастие, его следует понимать применительно к любому из родителей.

Сводка построений по расширенной симметрии

46 однородных полихор, построенных из A₄, B₄, F₄, H₄ симметрии представлены в этой таблице их полной расширенной симметрией и диаграммами Кокстера. Чередования сгруппированы по их киральной симметрии. Приведены все варианты, хотя курносый 24-элементный, с его 3 семейством конструкций - единственное, что является однородным. Счетчики в скобках либо повторяются, либо неоднородны. Диаграммы Кокстера даны с индексами от 1 до 46. Включено семейство дуопризматических 3-3 и 4-4, второе из-за его связи с B₄ семья.

Группа Кокстера	Расширенный симметрия	Полихора		Хиральный расширенный симметрия	Чередование сот
[3,3,3]	[3,3,3] (заказ 120)	6	₍₁₎ \| ₍₂₎ \| ₍₃₎ ₍₄₎ \| ₍₇₎ \| ₍₈₎
[3,3,3]	[2⁺[3,3,3]] (заказ 240)	3	₍₅₎\| ₍₆₎ \| ₍₉₎	[2⁺[3,3,3]]⁺ (заказ 120)	(1)	₍₋₎
[3,3^1,1]	[3,3^1,1] (заказ 192)	0	(никто)
	[1[3,3^1,1]]=[4,3,3] = (заказ 384)	(4)	₍₁₂₎ \| ₍₁₇₎ \| ₍₁₁₎ \| ₍₁₆₎
	[3[3^1,1,1]]=[3,4,3] = (заказ 1152)	(3)	₍₂₂₎ \| ₍₂₃₎ \| ₍₂₄₎	[3[3,3^1,1]]⁺ =[3,4,3]⁺ (заказ 576)	(1)	₍₃₁₎ (= ) ₍₋₎
[4,3,3]	[3[1⁺,4,3,3]]=[3,4,3] = (заказ 1152)	(3)	₍₂₂₎ \| ₍₂₃₎ \| ₍₂₄₎
	[4,3,3] (заказ 384)	12	₍₁₀₎ \| ₍₁₁₎ \| ₍₁₂₎ \| ₍₁₃₎ \| ₍₁₄₎ ₍₁₅₎ \| ₍₁₆₎ \| ₍₁₇₎ \| ₍₁₈₎ \| ₍₁₉₎ ₍₂₀₎ \| ₍₂₁₎	[1⁺,4,3,3]⁺ (заказ 96)	(2)	₍₁₂₎ (= ) ₍₃₁₎ ₍₋₎
	[4,3,3] (заказ 384)	12		[4,3,3]⁺ (заказ 192)	(1)	₍₋₎
[3,4,3]	[3,4,3] (заказ 1152)	6	₍₂₂₎ \| ₍₂₃₎ \| ₍₂₄₎ ₍₂₅₎ \| ₍₂₈₎ \| ₍₂₉₎	[2⁺[3⁺,4,3⁺]] (заказ 576)	1	₍₃₁₎
[3,4,3]	[2⁺[3,4,3]] (заказ 2304)	3	₍₂₆₎ \| ₍₂₇₎ \| ₍₃₀₎	[2⁺[3,4,3]]⁺ (заказ 1152)	(1)	₍₋₎
[5,3,3]	[5,3,3] (заказ 14400)	15	₍₃₂₎ \| ₍₃₃₎ \| ₍₃₄₎ \| ₍₃₅₎ \| ₍₃₆₎ ₍₃₇₎ \| ₍₃₈₎ \| ₍₃₉₎ \| ₍₄₀₎ \| ₍₄₁₎ ₍₄₂₎ \| ₍₄₃₎ \| ₍₄₄₎ \| ₍₄₅₎ \| ₍₄₆₎	[5,3,3]⁺ (заказ 7200)	(1)	₍₋₎
[3,2,3]	[3,2,3] (заказ 36)	0	(никто)	[3,2,3]⁺ (заказ 18)	0	(никто)
	[2⁺[3,2,3]] (заказ 72)	0		[2⁺[3,2,3]]⁺ (заказ 36)	0	(никто)
	[[3],2,3]=[6,2,3] = (заказ 72)	1		[1[3,2,3]]=[[3],2,3]⁺=[6,2,3]⁺ (заказ 36)	(1)
	[(2⁺,4)[3,2,3]]=[2⁺[6,2,6]] = (заказ 288)	1		[(2⁺,4)[3,2,3]]⁺=[2⁺[6,2,6]]⁺ (заказ 144)	(1)
[4,2,4]	[4,2,4] (заказ 64)	0	(никто)	[4,2,4]⁺ (заказ 32)	0	(никто)
	[2⁺[4,2,4]] (заказ 128)	0	(никто)	[2⁺[(4,2⁺,4,2⁺)]] (заказ 64)	0	(никто)
	[(3,3)[4,2*,4]]=[4,3,3] = (заказ 384)	(1)	₍₁₀₎	[(3,3)[4,2*,4]]⁺=[4,3,3]⁺ (заказ 192)	(1)	₍₁₂₎
	[[4],2,4]=[8,2,4] = (заказ 128)	(1)		[1[4,2,4]]=[[4],2,4]⁺=[8,2,4]⁺ (заказ 64)	(1)
	[(2⁺,4)[4,2,4]]=[2⁺[8,2,8]] = (заказ 512)	(1)		[(2⁺,4)[4,2,4]]⁺=[2⁺[8,2,8]]⁺ (заказ 256)	(1)

Смотрите также

Конечные правильные косые многогранники четырехмерного пространства
Выпуклые однородные соты - связанные бесконечные 4-многогранники в трехмерном евклидовом пространстве.
Выпуклые однородные соты в гиперболическом пространстве - связанные бесконечные 4-многогранники в трехмерном гиперболическом пространстве.
Паракомпактные однородные соты

использованная литература

^ N.W. Джонсон: Геометрии и преобразования, (2018) ISBN 978-1-107-10340-5 Глава 11: Конечные группы симметрии, 11.1 Многогранники и соты, стр.224
^ Т. Госсет: О регулярных и полурегулярных фигурах в пространстве n измерений, Вестник математики, Macmillan, 1900 г.
^ «Архивная копия» (PDF). Архивировано из оригинал (PDF) на 2009-12-29. Получено 2010-08-13.CS1 maint: заархивированная копия как заголовок (ссылка на сайт)
^ Элте (1912)
^ https://web.archive.org/web/19981206035238/http://members.aol.com/Polycell/uniform.html 6 декабря 1998 г. старейший архив
^ Универсальная книга математики: от абракадабры до парадоксов Зенона Дэвид Дарлинг, (2004) ASIN: B00SB4TU58
^ ^а ^б ^c ^d ^е ^ж ^г ^час ^я ^j ^k Джонсон (2015), глава 11, раздел 11.5 Сферические группы Кокстера, 11.5.5 полные полихорические группы
^ Равномерные многогранники в четырех измерениях, Георгий Ольшевский.
^ Мёллер, Марко (2004). Vierdimensionale Archimedische Polytope (PDF) (Докторская диссертация) (на немецком языке). Гамбургский университет.
^ Конвей (2008)
^ [1] Выпуклые и абстрактные многогранники мастер-класс (2005), Н. Джонсон - Аннотация "Равномерная полихора"
^ «Равномерная полихора». www.polytope.net. Получено 20 февраля, 2020.
^ Кокстер, Правильные многогранники, 7.7 Критерий Шлефли уравнение 7.78, стр.135
^ http://www.bendwavy.org/klitzing/incmats/s3s3s3s.htm
^ http://www.bendwavy.org/klitzing/incmats/s3s3s4s.htm
^ http://www.bendwavy.org/klitzing/incmats/s3s4s3s.htm
^ http://www.bendwavy.org/klitzing/incmats/s3s3s5s.htm
^ H.S.M. Кокстер, Правильные и полурегулярные многогранники II, [Math. Zeit. 188 (1985) с. 582-588 2,7 Четырехмерные аналоги курносого куба
^ http://bendwavy.org/klitzing/explain/polytope-tree.htm#scaliform
^ http://bendwavy.org/klitzing/incmats/tut=invtut.htm
^ Категория S1: простые скалиформы Туткап
^ http://bendwavy.org/klitzing/incmats/prissi.htm
^ Категория S3: специальные скалиформы Присси

А. Буль Стотт: Геометрическое выведение полуправильных из правильных многогранников и заполнения пространств, Верханделинген академии Конинклийке van Wetenschappen, ширина блока Амстердам, Eerste Sectie 11,1, Амстердам, 1910 г.

Б. Грюнбаум Выпуклые многогранники, Нью-Йорк ; Лондон: Springer, c2003. ISBN 0-387-00424-6.
Второе издание подготовил Фолькер Кайбель, Виктор Клее, и Гюнтер М. Циглер.
Элте, Э. Л. (1912), Полурегулярные многогранники гиперпространств, Гронинген: Университет Гронингена, ISBN 1-4181-7968-X [3] [4]
H.S.M. Coxeter:
- H.S.M. Кокстер, М. Longuet-Higgins und J.C.P. Миллер: Однородные многогранники, Философские труды Лондонского королевского общества, Лондон, 1954 г.
- H.S.M. Кокстер, Правильные многогранники, 3-е издание, Довер, Нью-Йорк, 1973
Калейдоскопы: Избранные произведения Х.С.М. Coxeter, отредактированный Ф. Артуром Шерком, Питером Макмалленом, Энтони С. Томпсоном, Азией Ивичем Вайс, публикацией Wiley-Interscience, 1995, ISBN 978-0-471-01003-6
- (Документ 22) Х.С.М. Кокстер, Регулярные и полурегулярные многогранники I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
- (Документ 23) Х.С.М. Кокстер, Правильные и полурегулярные многогранники II, [Math. Zeit. 188 (1985) 559-591]
- (Документ 24) Х.С.М. Кокстер, Правильные и полурегулярные многогранники III, [Math. Zeit. 200 (1988) 3-45]
H.S.M. Кокстер и У. О. Дж. Мозер. Генераторы и соотношения для дискретных групп 4-е изд., Springer-Verlag. Нью-Йорк. 1980 г. 92, стр. 122.
Джон Х. Конвей, Хайди Берджель, Хаим Гудман-Штраус, Симметрии вещей 2008, ISBN 978-1-56881-220-5 (Глава 26)
Джон Х. Конвей и M.J.T. Парень: Четырехмерные архимедовы многогранники, Труды коллоквиума по выпуклости в Копенгагене, стр. 38 и 39, 1965 г.
N.W. Джонсон: Теория однородных многогранников и сот, Кандидат наук. Диссертация, Университет Торонто, 1966 г.
N.W. Джонсон: Геометрии и преобразования, (2015) Глава 11: Конечные группы симметрии
Ричард Клитцинг, Снабжения, чередующиеся фасетки и диаграммы Стотта-Кокстера-Дынкина, Симметрия: культура и наука, Vol. 21, № 4, 329-344, (2010) [5]
Схоут, Питер Хендрик (1911), «Аналитическое рассмотрение многогранников, регулярно получаемых из правильных многогранников», Verhandelingen der Koninklijke Akademie van Wetenschappen Te Amsterdam, 11 (3): 87 п. Googlebook, 370-381

внешние ссылки

Выпуклые равномерные 4-многогранники
- Равномерные выпуклые многогранники в четырех измерениях, Марко Мёллер (на немецком)
- Равномерные многогранники в четырех измерениях, Георгий Ольшевский.
  1. Выпуклая однородная полихора на основе пентахороны, Георгий Ольшевский.
  2. Выпуклая однородная полихора на основе тессеракта / 16 ячеек, Георгий Ольшевский.
  3. Выпуклая однородная полихора на основе 24-х элементной, Георгий Ольшевский.
  4. Выпуклая однородная полихора на основе 120/600 клеток, Георгий Ольшевский.
  5. Аномально выпуклый однородный полихорон: (большая антипризма), Георгий Ольшевский.
  6. Выпуклая однородная призматическая полихора, Георгий Ольшевский.
  7. Равномерная полихора, полученная из гломерного тетраэдра B4, Георгий Ольшевский.
- Регулярные и полурегулярные выпуклые многогранники краткий исторический обзор
- Апплеты Java3D с исходниками
Невыпуклые равномерные 4-многогранники
- Равномерная полихора Джонатан Бауэрс
- Stella4D Стелла (программное обеспечение) создает интерактивные виды известных однородных полихор, включая 64 выпуклые формы и бесконечные призматические семейства.
Клитцинг, Ричард. "4D однородные многогранники".
4D-многогранники и их двойственные многогранники группы Кокстера W (A4), представленные кватернионами Международный журнал геометрических методов в современной физике, Vol. 9, No. 4 (2012) Мехмет Коджа, Назифе Оздес Коджа, Мудхахир Аль-Аджми (2012) [6]

Фундаментальный выпуклый регулярный и однородные многогранники в размерах 2–10
Семья	А_п	B_п	я₂(п) / D_п	E₆ / E₇ / E₈ / F₄ / г₂	ЧАС_п
Правильный многоугольник	Треугольник	Квадрат	п-угольник	Шестиугольник	Пентагон
Равномерный многогранник	Тетраэдр	Октаэдр • Куб	Демикуб		Додекаэдр • Икосаэдр
Равномерный 4-многогранник	5-элементный	16 ячеек • Тессеракт	Demitesseract	24-элементный	120 ячеек • 600 ячеек
Равномерный 5-многогранник	5-симплекс	5-ортоплекс • 5-куб	5-полукруглый
Равномерный 6-многогранник	6-симплекс	6-ортоплекс • 6-куб	6-полукуб	1₂₂ • 2₂₁
Равномерный 7-многогранник	7-симплекс	7-ортоплекс • 7-куб	7-полукруглый	1₃₂ • 2₃₁ • 3₂₁
Равномерный 8-многогранник	8-симплекс	8-ортоплекс • 8-куб	8-полукруглый	1₄₂ • 2₄₁ • 4₂₁
Равномерный 9-многогранник	9-симплекс	9-ортоплекс • 9-куб	9-полукруглый
Равномерный 10-многогранник	10-симплекс	10-ортоплекс • 10-куб	10-полукуб
Униформа п-многогранник	п-симплекс	п-ортоплекс • п-куб	п-полукуб	1_k2 • 2_k1 • k₂₁	п-пятиугольный многогранник
Темы: Семейства многогранников • Правильный многогранник • Список правильных многогранников и соединений

[1] N.W. Джонсон: Геометрии и преобразования, (2018) ISBN 978-1-107-10340-5 Глава 11: Конечные группы симметрии, 11.1 Многогранники и соты, стр.224

[2] Т. Госсет: О регулярных и полурегулярных фигурах в пространстве n измерений, Вестник математики, Macmillan, 1900 г.

[3] «Архивная копия» (PDF). Архивировано из оригинал (PDF) на 2009-12-29. Получено 2010-08-13.CS1 maint: заархивированная копия как заголовок (ссылка на сайт)

[4] Элте (1912)

[5] ttps://web.archive.org/web/19981206035238/http://members.aol.com/Polycell/uniform.html 6 декабря 1998 г. старейший архив

[6] Универсальная книга математики: от абракадабры до парадоксов Зенона Дэвид Дарлинг, (2004) ASIN: B00SB4TU58

[polychoric_groups-7] а ^б ^c ^d ^е ^ж ^г ^час ^я ^j ^k Джонсон (2015), глава 11, раздел 11.5 Сферические группы Кокстера, 11.5.5 полные полихорические группы

[8] Равномерные многогранники в четырех измерениях, Георгий Ольшевский.

[9] Мёллер, Марко (2004). Vierdimensionale Archimedische Polytope (PDF) (Докторская диссертация) (на немецком языке). Гамбургский университет.

[10] Конвей (2008)

[11] [1] Выпуклые и абстрактные многогранники мастер-класс (2005), Н. Джонсон - Аннотация "Равномерная полихора"

[:0-12] «Равномерная полихора». www.polytope.net. Получено 20 февраля, 2020.

[13] Кокстер, Правильные многогранники, 7.7 Критерий Шлефли уравнение 7.78, стр.135

[14] ttp://www.bendwavy.org/klitzing/incmats/s3s3s3s.htm

[15] ttp://www.bendwavy.org/klitzing/incmats/s3s3s4s.htm

[16] ttp://www.bendwavy.org/klitzing/incmats/s3s4s3s.htm

[17] ttp://www.bendwavy.org/klitzing/incmats/s3s3s5s.htm

[18] H.S.M. Кокстер, Правильные и полурегулярные многогранники II, [Math. Zeit. 188 (1985) с. 582-588 2,7 Четырехмерные аналоги курносого куба

[19] ttp://bendwavy.org/klitzing/explain/polytope-tree.htm#scaliform

[20] ttp://bendwavy.org/klitzing/incmats/tut=invtut.htm

[21] Категория S1: простые скалиформы Туткап

[22] ttp://bendwavy.org/klitzing/incmats/prissi.htm

[23] Категория S3: специальные скалиформы Присси

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

3-3	3-4	3-5	3-6	3-7	3-8
4-3	4-4	4-5	4-6	4-7	4-8
5-3	5-4	5-5	5-6	5-7	5-8
6-3	6-4	6-5	6-6	6-7	6-8
7-3	7-4	7-5	7-6	7-7	7-8
8-3	8-4	8-5	8-6	8-7	8-8

3-3	3-4	3-5	3-6	3-7	3-8
4-3	4-4	4-5	4-6	4-7	4-8
5-3	5-4	5-5	5-6	5-7	5-8
6-3	6-4	6-5	6-6	6-7	6-8
7-3	7-4	7-5	7-6	7-7	7-8
8-3	8-4	8-5	8-6	8-7	8-8