Конфигурация вершины - Vertex configuration
 Икосододекаэдр |  Фигура вершины представлен как 3.5.3.5 или (3.5)2 |
В геометрия, а конфигурация вершины[1][2][3][4] сокращенное обозначение для представления вершина фигуры многогранника или мозаики как последовательность граней вокруг вершины. За равномерные многогранники существует только один тип вершины, поэтому конфигурация вершин полностью определяет многогранник. (Хиральный многогранники существуют в парах зеркального отображения с одинаковой конфигурацией вершин.)
Конфигурация вершины задается как последовательность чисел, представляющих количество сторон граней, идущих вокруг вершины. Обозначение "a.b.c"описывает вершину, вокруг которой есть 3 грани, грани с а, б, и c стороны.
Например, «3.5.3.5» указывает вершину, принадлежащую 4 граням, чередующимся треугольники и пятиугольники. Эта конфигурация вершин определяет вершинно-транзитивный икосододекаэдр. Обозначения циклические и, следовательно, эквивалентны с разными начальными точками, поэтому 3.5.3.5 совпадает с 5.3.5.3. Порядок важен, поэтому 3.3.5.5 отличается от 3.5.3.5. (Первый состоит из двух треугольников, за которыми следуют два пятиугольника.) Повторяющиеся элементы могут быть собраны как экспоненты, поэтому этот пример также представлен как (3.5)2.
Его по-разному называли описание вершины,[5][6][7] тип вершины,[8][9] символ вершины,[10][11] расположение вершин,[12] шаблон вершин,[13] лицо-вектор.[14] Его также называют Канди и символ Роллетта за его использование для Архимедовы тела в своей книге 1952 года Математические модели.[15][16][17]
Фигуры вершин
А конфигурация вершины также можно представить как многоугольный вершина фигуры показывая лица вокруг вершины. Этот вершина фигуры имеет трехмерную структуру, поскольку грани не лежат в одной плоскости для многогранников, а для однородные по вершинам многогранники все соседние вершины находятся в одной плоскости, поэтому проекция на самолет может использоваться для визуального представления конфигурации вершины.
Вариации и использование
{3,3} = 33 Дефект 180 ° |  {3,4} = 34 Дефект 120 ° |  {3,5} = 35 Дефект 60 ° |  {3,6} = 36 |
 {4,3} Дефект 90 ° |  {4,4} = 44 |  {5,3} = 53 Дефект 36 ° |  {6,3} = 63 |
| Вершина требует не менее 3 граней и угловой дефект. Угловой дефект 0 ° заполнит евклидову плоскость правильной мозаикой. К Теорема Декарта, количество вершин 720 ° /дефект (4π радиан /дефект). | |||
Используются разные обозначения, иногда с разделителями запятой (,), а иногда и точкой (.). Оператор периода полезен, потому что он выглядит как произведение, и можно использовать нотацию экспоненты. Например, 3.5.3.5 иногда записывается как (3.5)2.
Обозначения также можно рассматривать как расширенную форму простого Символ Шлефли за правильные многогранники. Обозначение Шлефли {п,q} средства q п-угольники вокруг каждой вершины. Так {п,q} можно записать как п.п.п. ... (q раз) или пq. Например, икосаэдр равен {3,5} = 3.3.3.3.3 или 35.
Это обозначение применимо как к многоугольным мозаикам, так и к многогранникам. Плоская конфигурация вершин обозначает равномерное замощение, так же как неплоская конфигурация вершин обозначает однородный многогранник.
Обозначения неоднозначны для хиральный формы. Например, курносый куб имеет форму по часовой стрелке и против часовой стрелки, которые идентичны на всех зеркальных изображениях. Оба имеют конфигурацию вершин 3.3.3.3.4.
Звездные многоугольники
Обозначения также применимы для невыпуклых правильных граней, звездные многоугольники. Например, пентаграмма имеет символ {5/2}, что означает, что он имеет 5 сторон, дважды обходящих центр.
Например, есть 4 правильных звездных многогранника с правильными многоугольниками или фигурами вершин звездного многоугольника. В малый звездчатый додекаэдр имеет Символ Шлефли из {5 / 2,5}, который расширяется до явной конфигурации вершин 5 / 2,5 / 2,5 / 2,5 / 2,5 / 2 или объединяется как (5/2)5. В большой звездчатый додекаэдр, {5 / 2,3} имеет треугольную вершину и конфигурацию (5 / 2,5 / 2,5 / 2) или (5/2)3. В большой додекаэдр, {5,5 / 2} имеет фигуру пентаграммы вершины, с конфигурация вершины равно (5.5.5.5.5) / 2 или (55) / 2. А большой икосаэдр, {3,5 / 2} также имеет пентаграммическую вершинную фигуру с конфигурацией вершин (3.3.3.3.3) / 2 или (35)/2.
 |  | 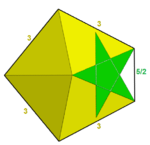 |  |  |
| {5/2,5} = (5/2)5 | {5/2,3} = (5/2)3 | 34.5/2 | 34.5/3 | (34.5/2)/2 |
|---|---|---|---|---|
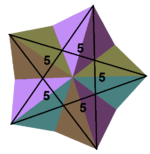 |  |  |  |  |
| {5,5/2} = (55)/2 | {3,5/2} = (35)/2 | V.34.5/2 | V34.5/3 | V (34.5/2)/2 |
Инвертированные полигоны
Считается, что грани вершинной фигуры движутся в одном направлении. Некоторые равномерные многогранники имеют фигуры вершин с инверсиями, где грани прогрессируют ретроградно. Фигура вершины представляет это в звездный многоугольник обозначение сторон п / д такой, что п<2q, куда п это количество сторон и q количество витков по кругу. Например, «3/2» означает треугольник, вершины которого повторяются дважды, что совпадает с одним поворотом назад. Точно так же «5/3» - обратная пентаграмма 5/2.
Все равномерные конфигурации вершин правильных выпуклых многоугольников
Полуправильные многогранники имеют конфигурации вершин с положительным угловой дефект.
ПРИМЕЧАНИЕ. Фигура вершины может представлять собой регулярную или полурегулярную мозаику на плоскости, если ее дефект равен нулю. Он может представлять собой замощение гиперболической плоскости, если его дефект отрицательный.
Для однородных многогранников дефект угла может использоваться для вычисления количества вершин. Теорема Декарта утверждает, что сумма всех угловых дефектов в топологической сфере должна составлять 4π радианы или 720 градусов.
Поскольку все однородные многогранники имеют одинаковые вершины, это соотношение позволяет нам вычислить количество вершин, которое составляет 4π/дефект или720 /дефект.
Пример: A усеченный куб 3.8.8 имеет угловой дефект 30 градусов. Следовательно, он имеет720/30 = 24 вершины.
В частности, следует, что {а,б} имеет 4 / (2 - б(1 - 2/а)) вершины.
Каждая нумерованная конфигурация вершин потенциально однозначно определяет полуправильный многогранник. Однако возможны не все конфигурации.
Топологические требования ограничивают существование. Конкретно p.q.r означает, что п-гон окружен чередующимися q-угольники и р-угольники, так что либо п даже или q равно р. по аналогии q даже или п равно р, и р даже или п равно q. Следовательно, потенциально возможными тройками являются 3.3.3, 3.4.4, 3.6.6, 3.8.8, 3.10.10, 3.12.12, 4.4.п (для любого п> 2), 4.6.6, 4.6.8, 4.6.10, 4.6.12, 4.8.8, 5.5.5, 5.6.6, 6.6.6. Фактически, все эти конфигурации с тремя гранями, встречающимися в каждой вершине, оказываются существующими.
Число в скобках - это количество вершин, определяемое угловым дефектом.
- Тройки
- Платоновы тела 3.3.3 (4), 4.4.4 (8), 5.5.5 (20)
- призмы 3.4.4 (6), 4.4.4 (8; также указано выше), 4.4.п (2п)
- Архимедовы тела 3.6.6 (12), 3.8.8 (24), 3.10.10 (60), 4.6.6 (24), 4.6.8 (48), 4.6.10 (120), 5.6.6 (60).
- обычная черепица 6.6.6
- полуправильные мозаики 3.12.12, 4.6.12, 4.8.8
- Четверки
- Платоново твердое тело 3.3.3.3 (6)
- антипризмы 3.3.3.3 (6; также указано выше), 3.3.3.п (2п)
- Архимедовы тела 3.4.3.4 (12), 3.5.3.5 (30), 3.4.4.4 (24), 3.4.5.4 (60)
- обычная черепица 4.4.4.4
- полуправильные мозаики 3.6.3.6, 3.4.6.4
- Пятерки
- Платоново твердое тело 3.3.3.3.3 (12)
- Архимедовы тела 3.3.3.3.4 (24), 3.3.3.3.5 (60) (оба хиральный )
- полуправильные мозаики 3.3.3.3.6 (хиральный), 3.3.3.4.4, 3.3.4.3.4 (обратите внимание, что два разных порядка одних и тех же чисел дают два разных образца)
- Шестерки
- обычная черепица 3.3.3.3.3.3
Конфигурация лица
Равномерное двойное или Каталонские твердые вещества, в том числе бипирамиды и трапецоэдры, находятся вертикально-правильный (лицо переходный ), и поэтому их можно идентифицировать с помощью аналогичных обозначений, которые иногда называют конфигурация лица.[3] Канди и Роллетт добавили к этим двойным символам префикс V. В отличие, Плитки и узоры использует квадратные скобки вокруг символа для равногранных мозаик.
Это обозначение представляет собой последовательный подсчет количества лиц, существующих на каждом вершина вокруг лицо.[18] Например, V3.4.3.4 или V (3.4)2 представляет ромбический додекаэдр который является лицом транзитивным: каждое лицо является ромб, а чередующиеся вершины ромба содержат по 3 или 4 грани.
Примечания
- ^ Равномерное решение для равномерных многогранников. В архиве 2015-11-27 на Wayback Machine (1993)
- ^ Равномерные многогранники Роман Э. Мейдер (1995)
- ^ а б Кристаллография квазикристаллов: концепции, методы и структуры. Вальтер Штюрер, София Делуди, (2009), стр. 18–20 и 51–53
- ^ Физическое металловедение: набор из 3 томов, том 1 под редакцией Дэвида Э. Лафлина, (2014), стр. 16–20
- ^ Архимедовы многогранники Стивен Датч
- ^ Однородные многогранники Джим Макнил
- ^ Однородные многогранники и двойственные к ним Роберт Уэбб
- ^ Графы типа симметрии платоновых и архимедовых тел, Юрий Кович, (2011)
- ^ 3. Общие теоремы: регулярные и полурегулярные мозаики. Кевин Митчелл, 1995
- ^ Ресурсы для преподавания дискретной математики: школьные проекты, история, модули и статьи под редакцией Брайана Хопкинса
- ^ Символ вершины Роберт Уиттакер
- ^ Структура и форма в дизайне: ключевые идеи для творческой практики Майкл Ханн
- ^ Графы типа симметрии платоновых и архимедовых тел Юрий Кович
- ^ Деза, Мишель; Штогрин, Михаил (1999). «Равномерные разбиения трехмерного пространства, их родственники и вложения». arXiv:математика / 9906034. Bibcode:1999математика ...... 6034D. Цитировать журнал требует
| журнал =(помощь) - ^ Вайсштейн, Эрик В. «Архимедово твердое тело». MathWorld.
- ^ Разделенные сферы: геодезические и упорядоченное деление сферы 6.4.1 Символ Канди-Роллетта, стр. 164
- ^ Лафлин (2014), стр. 16
- ^ Канди и Роллетт (1952)
Рекомендации
- Канди, Х. и Роллетт, А., Математические модели (1952), (3-е издание, 1989, Стрэдброк, Англия: Tarquin Pub.), 3,7 Архимедовы многогранники. Стр. 101–115, стр. 118–119 Таблица I, Сети архимедовых двойников, V.а.б.c... в качестве вертикально-правильный символы.
- Питер Кромвель, Многогранники, Cambridge University Press (1977) Архимедовы твердые тела. Стр. 156–167.
- Уильямс, Роберт (1979). Геометрическая основа естественной структуры: первоисточник дизайна. Dover Publications, Inc. ISBN 0-486-23729-X. Использует символ Канди-Роллетта.
- Грюнбаум, Бранко; Шепард, Г.С. (1987). Плитки и узоры. В. Х. Фриман и компания. ISBN 0-7167-1193-1. Стр. 58–64, Замощения правильных многоугольников a.b.c .... (Замощения правильными многоугольниками и звездчатыми многоугольниками) стр. 95–97, 176, 283, 614–620, Символ моноэдрального разбиения [v1.v2. ... .vр]. С. 632–642 полые мозаики.
- Симметрии вещей 2008, Джон Х. Конвей, Хайди Берджел, Хаим Гудман-Штрасс, ISBN 978-1-56881-220-5 (стр. 289 Фигуры вершин, используется разделитель запятой, для архимедовых тел и мозаик).

