Шестиугольная черепица - Википедия - Hexagonal tiling

Шестиугольная черепица

Тип	Обычная черепица
Конфигурация вершины	6.6.6 (или 6³)
Конфигурация лица	V3.3.3.3.3.3 (или V3⁶)
Символ (ы) Шлефли	{6,3} т {3,6}
Символ (ы) Wythoff	3 \| 6 2 2 6 \| 3 3 3 3 \|
Диаграмма (ы) Кокстера
Симметрия	p6m, [6,3], (*632)
Симметрия вращения	p6, [6,3]⁺, (632)
Двойной	Треугольная черепица
Характеристики	Вершинно-транзитивный, ребро-транзитивный, лицо переходный

В геометрия, то шестиугольная черепица или же гексагональная мозаика это обычная черепица из Евклидова плоскость, в котором три^{[требуется разъяснение ]} шестиугольники встречаются в каждой вершине. Она имеет Символ Шлефли из {6,3} или т{3,6} (в виде усеченной треугольной плитки).

Английский математик Джон Конвей назвал это гексилль.

Внутренний угол шестиугольника составляет 120 градусов, поэтому три шестиугольника в одной точке составляют полные 360 градусов. Это один из три правильных мозаики плоскости. Два других - это треугольная черепица и квадратная черепица.

Приложения

Шестиугольная мозаика - самый плотный способ устроить круги в двух измерениях. В Гипотеза о сотах утверждает, что шестиугольная мозаика - лучший способ разделить поверхность на области равной площади с наименьшим общим периметром. Оптимальная трехмерная структура для создания сот (а точнее, мыльных пузырей) была исследована Лорд Кельвин, которые считали, что Структура Кельвина (или же объемно-центрированный кубический решетка) оптимальна. Однако менее регулярные Структура Вира – Фелана немного лучше.

Эта структура существует естественным образом в виде графит, где каждый лист графен напоминает проволочную сетку с прочными ковалентными углеродными связями. Синтезированы трубчатые листы графена; они известны как углеродные нанотрубки. У них есть много потенциальных применений из-за их высокого предел прочности и электрические свойства. Силицен похож.

Куриная проволока состоит из гексагональной решетки (часто не правильной) из проволок.

Самый плотный упаковка круга расположен как шестиугольники в этой плитке
Куриная проволока ограждение
Графен
А углеродная нанотрубка можно рассматривать как мозаику шестиугольника на цилиндрический поверхность

Гексагональная мозаика появляется во многих кристаллах. В трех измерениях гранецентрированная кубическая и гексагональная плотная упаковка являются обычными кристаллическими структурами. Это самые плотные из известных сфер в трех измерениях, которые считаются оптимальными. Конструктивно они представляют собой параллельные слои гексагональных плиток, аналогичные структуре графита. Они различаются тем, как слои расположены в шахматном порядке, причем гранецентрированный кубик является более правильным из двух. Чистый медь среди других материалов образует гранецентрированную кубическую решетку.

Равномерная окраска

Есть три различных равномерные раскраски шестиугольной мозаики, все порожденные отражательной симметрией Конструкции Wythoff. (час,k) представляют собой периодическое повторение одной цветной плитки, считая гексагональные расстояния как час во-первых, и k второй. Такой же подсчет используется в Многогранники Гольдберга, с обозначением {п+,3}_час,k, и может применяться к гиперболическим мозаикам для п>6.

k-униформа	1-униформа			2-униформа		3-униформа
Симметрия	p6m, (* 632)		p3m1, (* 333)	p6m, (* 632)		п6, (632)
Рисунок
Цвета	1	2	3	2	4	2	7
(ч, к)	(1,0)	(1,1)		(2,0)		(2,1)
Schläfli	{6,3}	т {3,6}	т {3^[3]}
Wythoff	3 \| 6 2	2 6 \| 3	3 3 3 \|
Coxeter
Конвей	ЧАС	tΔ		cH = t6daH		wH = t6dsH

Трехцветная мозаика - это мозаика, созданная по порядку-3. пермутоэдры.

Шестиугольная черепица с фаской

А скошенный шестиугольная плитка заменяет края новыми шестиугольниками и превращается в другую шестиугольную плитку. В пределе исходные грани исчезают, а новые шестиугольники вырождаются в ромбы, и он становится ромбическая черепица.

Шестиугольники (H)	Шестиугольники с фаской (cH)			Ромби (daH)

Связанные мозаики

Шестиугольники можно разрезать на 6 треугольников. Этот процесс приводит к двум 2-однородные мозаики, а треугольная черепица:

Обычная черепица	Рассечение	2-однородные мозаики		Обычная черепица
Оригинал		1/3 рассечена	2/3 рассечено	полностью рассечен
Обычная черепица	Вставка	2-униформа Dual		Обычная черепица
Оригинал		1/3 вставка	2/3 вставка	полностью вставлен

Шестиугольную мозаику можно рассматривать как удлиненная ромбическая черепица, где каждая вершина ромбической мозаики растягивается на новое ребро. Это похоже на соотношение ромбический додекаэдр и ромбо-шестиугольный додекаэдр мозаика в 3-х измерениях.

Ромбическая черепица	Шестиугольная черепица	Фехтование использует это отношение

Также возможно разделить прототипы некоторых шестиугольных мозаик на два, три, четыре или девять равных пятиугольников:

Пятиугольная черепица тип 1 с накладками правильных шестиугольников (по 2 пятиугольника в каждом).	пятиугольная мозаика типа 3 с наложением правильных шестиугольников (по 3 пятиугольника в каждом).	Пятиугольная мозаика типа 4 с перекрытиями полуправильных шестиугольников (по 4 пятиугольника в каждом).	Пятиугольная черепица типа 3 с накладками двух размеров правильных шестиугольников (состоящих из 3 и 9 пятиугольников соответственно).

Мутации симметрии

Этот тайлинг топологически связан как часть последовательности регулярных мозаик с шестиугольник грани, начиная с шестиугольной мозаики, с Символ Шлефли {6, n} и Диаграмма Кокстера , прогрессирующая до бесконечности.

*п62 изменения симметрии правильных мозаик: {6,п} v т е
Сферический	Евклидово	Гиперболические мозаики
{6,2}	{6,3}	{6,4}	{6,5}	{6,6}	{6,7}	{6,8}	...	{6,∞}

Это разбиение топологически связано с правильными многогранниками с вершина фигуры п³, как часть последовательности, которая продолжается в гиперболическая плоскость.

*п32 изменения симметрии правильных мозаик: {п,3} v т е
Сферический				Евклидово	Компактная гиперболия.		Paraco.	Некомпактный гиперболический

{2,3}	{3,3}	{4,3}	{5,3}	{6,3}	{7,3}	{8,3}	{∞,3}	{12i, 3}	{9i, 3}	{6i, 3}	{3i, 3}

Аналогично это связано с униформой усеченный многогранники с вершиной п.6.6.

*п32 мутации симметрии усеченных мозаик: п.6.6 v т е
Сим. *п42 [n, 3]	Сферический				Евклид.	Компактный		Parac.	Некомпактный гиперболический
Сим. *п42 [n, 3]	*232 [2,3]	*332 [3,3]	*432 [4,3]	*532 [5,3]	*632 [6,3]	*732 [7,3]	*832 [8,3]...	*∞32 [∞,3]	[12i, 3]	[9i, 3]	[6i, 3]
Усеченный цифры
Конфиг.	2.6.6	3.6.6	4.6.6	5.6.6	6.6.6	7.6.6	8.6.6	∞.6.6	12i.6.6	9i.6.6	6i.6.6
н-кис цифры
Конфиг.	V2.6.6	V3.6.6	V4.6.6	V5.6.6	V6.6.6	V7.6.6	V8.6.6	V∞.6.6	V12i.6.6	V9i.6.6	V6i.6.6

Эта мозаика также является частью последовательности усеченных ромбических многогранников и мозаик с [n, 3] Группа Коксетера симметрия. Куб можно рассматривать как ромбический шестигранник, в котором ромбы представляют собой квадраты. У усеченных форм есть правильные n-угольники в усеченных вершинах и нерегулярные шестиугольные грани.

Мутации симметрии двойственных квазирегулярных мозаик: V (3.n)²
* n32	Сферический			Евклидово	Гиперболический
* n32	*332	*432	*532	*632	*732	*832...	*∞32
Плитка
Конф.	В (3,3)²	V (3,4)²	В (3,5)²	В (3,6)²	В (3,7)²	V (3.8)²	V (3.∞)²

Конструкции Wythoff из шестиугольных и треугольных мозаик

Словно равномерные многогранники есть восемь однородные мозаики который может быть основан на правильном шестиугольном тайлинге (или двойственном треугольная черепица ).

Нарисовывая плитки красного цвета на исходных гранях, желтого цвета в исходных вершинах и синего цвета вдоль исходных краев, можно получить 8 форм, 7 из которых топологически различны. (The усеченная треугольная мозаика топологически идентична шестиугольной мозаике.)

Однородные шестиугольные / треугольные мозаики
Фундаментальный домены	Симметрия: [6,3], (*632)							[6,3]⁺, (632)
	{6,3}	т {6,3}	г {6,3}	т {3,6}	{3,6}	рр {6,3}	tr {6,3}	sr {6,3}


Конфиг.	6³	3.12.12	(6.3)²	6.6.6	3⁶	3.4.6.4	4.6.12	3.3.3.3.6

Моноэдральные выпуклые шестиугольные мозаики

Существует 3 типа моноэдральных выпуклых шестиугольных мозаик.^[1] Они все равногранный. У каждого есть параметрические вариации в пределах фиксированной симметрии. Тип 2 содержит скользящие отражения, и является 2-изоэдральным, сохраняя киральные пары различными.

3 типа моноэдральных выпуклых шестиугольных мозаик
1	2		3
п2, 2222	пгг, 22 ×	п2, 2222	п3, 333

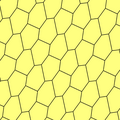б = е B + C + D = 360 °	б = д, д = е B + C + E = 360 °		а = е, б = с, г = е B = D = F = 120 °
2-х плитная решетка	Решетка из 4 плиток		Решетка из 3 плиток

Топологически эквивалентные мозаики

Гексагональные мозаики могут быть построены с той же топологией {6,3}, что и обычные мозаики (3 шестиугольника вокруг каждой вершины). Существует 13 вариантов с изоэдральными гранями. Приведенная симметрия предполагает, что все грани одного цвета. Цвета здесь обозначают позиции решетки.^[2] Одноцветные (1-плитки) решетки бывают параллелогон шестиугольники.

13 изоэдрально-черепичных шестиугольников
пг (× ×)	п3 (333)	pmg (22 *)

пгг (22 ×)	p31m (3 * 3)	p2 (2222)	см (2 * 22)	p6m (* 632)

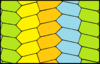Другие изоэдрально-мозаичные топологические шестиугольные мозаики рассматриваются как четырехугольники и пятиугольники, которые не стыкуются между собой, а интерпретируются как коллинеарные смежные ребра:

Четырехугольники, выложенные изогранной плиткой
pmg (22 *)		пгг (22 ×)			см (2 * 22)	p2 (2222)
Параллелограмм	Трапеция	Параллелограмм	Прямоугольник	Параллелограмм	Прямоугольник	Прямоугольник

Изогранные пятиугольники
p2 (2222)	пгг (22 ×)	п3 (333)

2-однородные и 3-однородные мозаики имеют вращательную степень свободы, которая искажает 2/3 шестиугольников, включая коллинеарный случай, который также можно рассматривать как мозаику шестиугольников и более крупных треугольников без стыков.^[3]

Это также может быть искажено в хиральный 4-х цветный трехсторонний узор, искажающий некоторые шестиугольники в параллелограммы. Плетеный узор с 2 цветными гранями имеет ротационные 632 (p6) симметрия. А шеврон узор имеет симметрию pmg (22 *), которая понижается до p1 (°) с 3 или 4 цветными плитками.

Обычный	Гиратированный	Обычный	Сотканный	Шеврон
p6m, (* 632)	п6, (632)	p6m (* 632)	p6 (632)	p1 (°)

p3m1, (* 333)	п3, (333)	p6m (* 632)	p2 (2222)	p1 (°)

Упаковка круга

Шестиугольную плитку можно использовать как упаковка круга, помещая круги равного диаметра в центре каждой точки. Каждый круг находится в контакте с 3 другими кругами в упаковке (номер поцелуя ).^[4] Зазор внутри каждого шестиугольника позволяет разместить один круг, создавая наиболее плотную упаковку из треугольная черепица, с каждым кругом контактируйте максимум 6 кругов.

Связанные регулярные сложные апейрогоны

Есть 2 регулярные сложные апейрогоны, разделяющие вершины шестиугольной мозаики. Регулярные сложные апейрогоны имеют вершины и ребра, причем ребра могут содержать 2 и более вершины. Обычные апейрогоны п{q}р ограничены: 1 /п + 2/q + 1/р = 1. Ребра имеют п вершины, а фигуры вершин - р-гональный.^[5]

Первый состоит из 2-х ребер, по три вокруг каждой вершины, второй - из шестиугольных ребер, по три вокруг каждой вершины. Третий комплексный апейрогон, имеющий одни и те же вершины, является квазирегулярным, в котором чередуются 2-ребра и 6-ребра.

2 {12} 3 или	6 {4} 3 или

Смотрите также

внешняя ссылка

ДНК | urlname = HexagonalGrid | title = Шестиугольная сетка}}
- Вайсштейн, Эрик В. «Обычная тесселяция». MathWorld.
- Вайсштейн, Эрик В. «Равномерная тесселяция». MathWorld.
Клитцинг, Ричард. "2D евклидовы мозаики o3o6x - гексат - O3".

v т е Фундаментальный выпуклый обычный и однородные соты в размерах 2-9
Космос	Семья	${ displaystyle { tilde {A}} _ {n-1}}$	${ displaystyle { tilde {C}} _ {n-1}}$	${ displaystyle { tilde {B}} _ {n-1}}$	${ displaystyle { tilde {D}} _ {n-1}}$	${ displaystyle { tilde {G}} _ {2}}$ / ${ displaystyle { tilde {F}} _ {4}}$ / ${ displaystyle { tilde {E}} _ {n-1}}$
E²	Равномерная черепица	{3^[3]}	δ₃	hδ₃	qδ₃	Шестиугольный
E³	Равномерно выпуклые соты	{3^[4]}	δ₄	hδ₄	qδ₄
E⁴	Равномерные 4-соты	{3^[5]}	δ₅	hδ₅	qδ₅	24-ячеечные соты
E⁵	Равномерные 5-соты	{3^[6]}	δ₆	hδ₆	qδ₆
E⁶	Равномерные 6-соты	{3^[7]}	δ₇	hδ₇	qδ₇	2₂₂
E⁷	Равномерные 7-соты	{3^[8]}	δ₈	hδ₈	qδ₈	1₃₃ • 3₃₁
E⁸	Равномерные 8-соты	{3^[9]}	δ₉	hδ₉	qδ₉	1₅₂ • 2₅₁ • 5₂₁
E⁹	Равномерные 9-соты	{3^[10]}	δ₁₀	hδ₁₀	qδ₁₀
E^п-1	Униформа (п-1)-соты	{3^[n]}	δ_п	hδ_п	qδ_п	1_k2 • 2_k1 • k₂₁

[1] Плитки и узоры, разд. 9.3 Другие моноэдральные мозаики выпуклыми многоугольниками

[2] Мозаики и узоры, из списка 107 равногранных мозаик, стр. 473–481.

[3] Плитки и узоры, равномерные мозаики без стыка

[Critchlow-4] Порядок в космосе: справочник по дизайну, Кейт Кричлоу, стр. 74–75, образец 2.

[5] Кокстер, Регулярные комплексные многогранники, с. 111-112, с. 136.

[1]

[2]

[3]

[4]

[5]