Усеченная тетрагексагональная мозаика - Truncated tetrahexagonal tiling

Усеченная тетрагексагональная мозаика
Модель диска Пуанкаре из гиперболическая плоскость
Тип	Гиперболическая равномерная мозаика
Конфигурация вершины	4.8.12
Символ Шлефли	tr {6,4} или ${ displaystyle t { begin {Bmatrix} 6 4 end {Bmatrix}}}$
Символ Wythoff	2 6 4 \|
Диаграмма Кокстера	или же
Группа симметрии	[6,4], (*642)
Двойной	Заказ-4-6 облицовка кисромбиллом
Характеристики	Вершинно-транзитивный

В геометрия, то усеченная тетрагексагональная мозаика является полуправильным замощением гиперболической плоскости. Есть один квадрат, один восьмиугольник, и один двенадцатигранник на каждой вершина. Она имеет Символ Шлефли тр {6,4}.

Двойная черепица


Двойственный тайлинг называется Заказ-4-6 мозаика кисромбилля, выполненный как полное деление пополам гексагональная черепица порядка 4, здесь треугольники показаны чередующимися цветами. Этот тайлинг представляет собой фундаментальные треугольные области симметрии [6,4] (* 642).

Связанные многогранники и мозаики

п42 мутации симметрии неусеченных мозаик: 4.8.2n* v т е
Симметрия *п42 [n, 4]	Сферический		Евклидово	Компактный гиперболический				Paracomp.
Симметрия *п42 [n, 4]	*242 [2,4]	*342 [3,4]	*442 [4,4]	*542 [5,4]	*642 [6,4]	*742 [7,4]	*842 [8,4]...	*∞42 [∞,4]
Усеченный фигура	4.8.4	4.8.6	4.8.8	4.8.10	4.8.12	4.8.14	4.8.16	4.8.∞
Усеченный двойники	V4.8.4	V4.8.6	V4.8.8	V4.8.10	V4.8.12	V4.8.14	V4.8.16	V4.8.∞

*nn2 мутации симметрии полностью усеченных мозаик: 4.2п.2п v т е
Симметрия *nn2 [п, п]	Сферический		Евклидово	Компактный гиперболический				Paracomp.
Симметрия *nn2 [п, п]	*222 [2,2]	*332 [3,3]	*442 [4,4]	*552 [5,5]	*662 [6,6]	*772 [7,7]	*882 [8,8]...	*∞∞2 [∞,∞]
Фигура
Конфиг.	4.4.4	4.6.6	4.8.8	4.10.10	4.12.12	4.14.14	4.16.16	4.∞.∞
Двойной
Конфиг.	V4.4.4	V4.6.6	V4.8.8	V4.10.10	V4.12.12	V4.14.14	V4.16.16	V4.∞.∞

Из Строительство Wythoff четырнадцать гиперболических однородные мозаики это может быть основано на регулярном гексагональном замощении четвертого порядка.

Рисуя плитки красного цвета на исходных гранях, желтого цвета в исходных вершинах и синего цвета вдоль исходных краев, мы получаем 7 форм с полной [6,4] симметрией и 7 с подсимметрией.

Равномерные тетрагексагональные мозаики v т е
*Симметрия: [6,4], (642 )** (с подсимметрией [6,6] (* 662), [(4,3,3)] (* 443), [∞, 3, ∞] (* 3222) индекса 2) (И [(∞, 3, ∞, 3)] (* 3232) подсимметрия индекса 4)
= = =	=	= = =	=	= = =	=

{6,4}	т {6,4}	г {6,4}	т {4,6}	{4,6}	rr {6,4}	tr {6,4}
Униформа двойников


V6⁴	V4.12.12	V (4,6)²	V6.8.8	V4⁶	V4.4.4.6	V4.8.12
Чередования
[1⁺,6,4] (*443)	[6⁺,4] (6*2)	[6,1⁺,4] (*3222)	[6,4⁺] (4*3)	[6,4,1⁺] (*662)	[(6,4,2⁺)] (2*32)	[6,4]⁺ (642)
=	=	=	=	=	=

ч {6,4}	с {6,4}	ч. {6,4}	с {4,6}	ч {4,6}	чрр {6,4}	sr {6,4}

Симметрия

Усеченная четырехгранная черепица с зеркальными линиями зеленого, красного и синего цветов:

Диаграммы симметрии для подгрупп малого индекса из [6,4], показанные в гексагональной трансляционной ячейке внутри {6,6} черепица, с основным доменом желтого цвета.

Двойник мозаики представляет фундаментальные области (* 642) орбифолд симметрия. Из симметрии [6,4] получается 15 подгрупп с малым индексом путем удаления зеркала и чередование операторы. Зеркала могут быть удалены, если все заказы его филиалов равны, что сокращает заказы соседних филиалов вдвое. Удаление двух зеркал оставляет точку вращения половинного порядка, где встречаются снятые зеркала. На этих изображениях уникальные зеркала окрашены в красный, зеленый и синий цвета, а треугольники, окрашенные попеременно, показывают расположение точек вращения. [6⁺,4⁺], (32 ×) имеет узкие линии, обозначающие отражения скольжения. В индекс подгруппы -8 группа, [1⁺,6,1⁺,4,1⁺] (3232) - это коммутаторная подгруппа из [6,4].

Большая подгруппа, построенная как [6,4 *], удаляющая точки вращения из [6,4⁺], (3 * 22), индекс 6 становится (*3333 ) и [6 *, 4], удалив точки инерции [6⁺, 4], (2 * 33), индекс 12 как (*222222 ). Наконец, их прямые подгруппы [6,4 *]⁺, [6*,4]⁺, индексы подгрупп 12 и 24 соответственно, могут быть даны в орбифолдной нотации как (3333) и (222222).

Подгруппы малых индексов в [6,4]
Индекс	1	2			4
Диаграмма
Coxeter	[6,4] =	[1⁺,6,4] =	[6,4,1⁺] =	[6,1⁺,4] =	[1⁺,6,4,1⁺] =	[6⁺,4⁺]
Орбифолд	*642	*443	*662	*3222	*3232	32×
Полупрямые подгруппы
Диаграмма
Coxeter		[6,4⁺]	[6⁺,4]	[(6,4,2⁺)]	[6,1⁺,4,1⁺] = = = =	[1⁺,6,1⁺,4] = = = =
Орбифолд		4*3	6*2	2*32	2*33	3*22
Прямые подгруппы
Индекс	2	4			8
Диаграмма
Coxeter	[6,4]⁺ =	[6,4⁺]⁺ =	[6⁺,4]⁺ =	[(6,4,2⁺)]⁺ =	[6⁺,4⁺]⁺ = [1⁺,6,1⁺,4,1⁺] = = =
Орбифолд	642	443	662	3222	3232
Радикальные подгруппы
Индекс		8	12	16	24
Диаграмма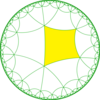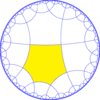
Coxeter		[6,4*] =	[6*,4]	[6,4*]⁺ =	[6*,4]⁺
Орбифолд		*3333	*222222	3333	222222