Диаграмма Кокстера – Дынкина - Coxeter–Dynkin diagram

Диаграммы Кокстера – Дынкина для фундаментальных конечных групп Кокстера

Диаграммы Кокстера – Дынкина для фундаментальных аффинных групп Кокстера

В геометрия, а Диаграмма Кокстера – Дынкина (или же Диаграмма Кокстера, Граф Кокстера) это график с цифровыми обозначениями ребер (называемых ветви), представляющие пространственные отношения между набором зеркала (или отражающий гиперплоскости ). Он описывает калейдоскопический конструкция: каждый «узел» графа представляет собой зеркало (домен грань ), а метка, прикрепленная к ветви, кодирует двугранный угол порядок между двумя зеркалами (на домене гребень ), то есть величина, на которую можно умножить угол между отражающими плоскостями, чтобы получить 180 градусов. Непомеченная ветвь неявно представляет третий порядок (60 градусов).

Каждая диаграмма представляет собой Группа Кокстера, и группы Кокстера классифицируются по связанным с ними диаграммам.

Диаграммы Дынкина являются тесно связанными объектами, которые отличаются от диаграмм Кокстера в двух отношениях: во-первых, ветви с меткой "4" и выше являются направленный, а диаграммы Кокстера имеют вид ненаправленный; во-вторых, диаграммы Дынкина должны удовлетворять дополнительному (кристаллографический ) ограничение, а именно, что разрешены только метки ветвей 2, 3, 4 и 6. Диаграммы Дынкина соответствуют и используются для классификации корневые системы и поэтому полупростые алгебры Ли.^[1]

Описание

Ветви диаграммы Кокстера – Дынкина помечены значком Рациональное число п, представляющий собой двугранный угол 180 ° /п. Когда $п = 2$ угол равен 90 °, и зеркала не взаимодействуют друг с другом, поэтому ответвление на схеме можно не указывать. Если ветка не помечена, предполагается, что она имеет $п = 3$ , представляющий угол 60 °. Два параллельных зеркала имеют ответвление, отмеченное знаком «∞». В принципе, п зеркала могут быть представлены полный график в котором все п( $п - 1) / 2$ ветви нарисованы. На практике почти все интересные конфигурации зеркал включают ряд прямых углов, поэтому соответствующие ветви опускаются.

Диаграммы могут быть помечены их графической структурой. Первые формы, изученные Людвиг Шлефли являются орто-схемы которые имеют линейные графики, которые генерируют правильные многогранники и обычные соты. Плагиосхемы находятся симплексы представлен графами ветвления, и циклосхемы симплексы, представленные циклическими графами.

Матрица Шлефли

Каждой диаграмме Кокстера соответствует Матрица Шлефли (назван так в честь Людвиг Шлефли ), с матричными элементами $а я, j = а j, я = -2cos (π / п)$ куда п - порядок ветвления между парами зеркал. Как матрица косинусов, его также называют Матрица грамиана после Йорген Педерсен Грам. Все Группа Кокстера Матрицы Шлефли симметричны, потому что их корневые векторы нормализованы. Это тесно связано с Матрица Картана, используемый в аналогичном, но ориентированном графе Диаграммы Дынкина в ограниченных случаях p = 2, 3, 4 и 6, которые в общем случае НЕ симметричны.

Определитель матрицы Шлефли, называемый Schläflian, а его знак определяет, является ли группа конечной (положительной), аффинной (нулевой), неопределенной (отрицательной). Это правило называется Критерий Шлефли.^[2]

В собственные значения матрицы Шлефли определяет, имеет ли группа Кокстера конечный тип (все положительно), аффинный тип (все неотрицательные, по крайней мере, один равен нулю), или неопределенный тип (иначе). Неопределенный тип иногда дополнительно подразделяется, например на гиперболические и другие группы Кокстера. Однако существует несколько неэквивалентных определений гиперболических групп Кокстера. Мы используем следующее определение: группа Кокстера со связной диаграммой - это гиперболический если она не имеет ни конечного, ни аффинного типа, но каждая собственная связная поддиаграмма имеет конечный или аффинный тип. Гиперболическая группа Кокстера - это компактный если все подгруппы конечны (т.е. имеют положительные детерминанты), и паракомпакт если все его подгруппы конечны или аффинны (т.е. имеют неотрицательные детерминанты).

Конечные и аффинные группы также называются эллиптический и параболический соответственно. Гиперболические группы также называются Ланнером в честь Ф. Ланнера, который перечислил компактные гиперболические группы в 1950 г.^[3] и Кошуля (или квази-Ланнара) для паракомпактных групп.

Группы Кокстера 2-го ранга

Для ранга 2 тип группы Кокстера полностью определяется определителем матрицы Шлефли, поскольку это просто произведение собственных значений: конечный тип (положительный определитель), аффинный тип (нулевой определитель) или гиперболический (отрицательный определитель) . Коксетер использует эквивалент скобка в котором перечислены последовательности порядков ветвления вместо графических диаграмм узел-ветвь. Рациональные решения [p / q], , также существуют, с gcd (p, q) = 1, которые определяют перекрывающиеся фундаментальные области. Например, 3/2, 4/3, 5/2, 5/3, 5/4. и 6/5.

Тип	Конечный					Аффинный	Гиперболический
Геометрия					...
Coxeter	[ ]	[2]	[3]	[4]	[п]	[∞]	[∞]	[iπ / λ]
Заказ	2	4	6	8	2п	∞
Зеркальные линии раскрашены в соответствии с узлами диаграммы Кокстера. Фундаментальные области окрашены попеременно.

Диаграммы групп Кокстера ранга 2
Заказ п	Группа	Диаграмма Кокстера		Матрица Шлефли
Заказ п	Группа	Диаграмма Кокстера		${displaystyle left [{egin {matrix} 2 & a_ {12} a_ {21} & 2end {matrix}} ight]}$	Детерминант (4-а₂₁* а₁₂)
Конечный (Определитель> 0)
2	я₂(2) = А₁xA₁		[2]	${displaystyle left [{egin {smallmatrix} 2 & 0 0 & 2end {smallmatrix}} ight]}$	4
3	я₂(3) = А₂		[3]	${displaystyle left [{egin {smallmatrix} 2 & -1 -1 & 2end {smallmatrix}} ight]}$	3
3/2			[3/2]	${displaystyle left [{egin {smallmatrix} 2 & 1 1 & 2end {smallmatrix}} ight]}$	3
4	я₂(4) = B₂		[4]	${displaystyle left [{egin {smallmatrix} 2 & - {sqrt {2}} - {sqrt {2}} & 2end {smallmatrix}} ight]}$	2
4/3			[4/3]	${displaystyle left [{egin {smallmatrix} 2 & {sqrt {2}} {sqrt {2}} & 2end {smallmatrix}} ight]}$	2
5	я₂(5) = H₂		[5]	${displaystyle left [{egin {smallmatrix} 2 & -phi -phi & 2end {smallmatrix}} ight]}$	${displaystyle (5- {sqrt {5}}) / 2}$ ~1.38196601125
5/4			[5/4]	${displaystyle left [{egin {smallmatrix} 2 & phi phi & 2end {smallmatrix}} ight]}$	${displaystyle (5- {sqrt {5}}) / 2}$ ~1.38196601125
5/2			[5/2]	${displaystyle left [{egin {smallmatrix} 2 & 1-phi 1-phi & 2end {smallmatrix}} ight]}$	${displaystyle (5+ {sqrt {5}}) / 2}$ ~3.61803398875
5/3			[5/3]	${displaystyle left [{egin {smallmatrix} 2 & phi -1 phi -1 & 2end {smallmatrix}} ight]}$	${displaystyle (5+ {sqrt {5}}) / 2}$ ~3.61803398875
6	я₂(6) = G₂		[6]	${displaystyle left [{egin {smallmatrix} 2 & - {sqrt {3}} - {sqrt {3}} & 2end {smallmatrix}} ight]}$	1
6/5			[6/5]	${displaystyle left [{egin {smallmatrix} 2 & {sqrt {3}} {sqrt {3}} & 2end {smallmatrix}} ight]}$	1
8	я₂(8)		[8]	${displaystyle left [{egin {smallmatrix} 2 & - {sqrt {2+ {sqrt {2}}}}} - {sqrt {2+ {sqrt {2}}}} & 2end {smallmatrix}} ight]}$	${displaystyle 2- {sqrt {2}}}$ ~0.58578643763
10	я₂(10)		[10]	${displaystyle left [{egin {smallmatrix} 2 & - {sqrt {(5+ {sqrt {5}}) / 2}} - {sqrt {(5+ {sqrt {5}}) / 2}} & 2end {smallmatrix }} ight]}$	${displaystyle (3- {sqrt {5}}) / 2}$ ~0.38196601125
12	я₂(12)		[12]	${displaystyle left [{egin {smallmatrix} 2 & - {sqrt {2+ {sqrt {3}}}}} - {sqrt {2+ {sqrt {3}}}} & 2end {smallmatrix}} ight]}$	${displaystyle 2- {sqrt {3}}}$ ~0.26794919243
п	я₂(п)		[п]	${displaystyle left [{egin {smallmatrix} 2 & -2cos (pi / p) - 2cos (pi / p) & 2end {smallmatrix}} ight]}$	${displaystyle 4sin ^ {2} (пи / р)}$
Аффинный (Определитель = 0)
∞	я₂(∞) = ${displaystyle {ilde {I}} _ {1}}$ = ${displaystyle {ilde {A}} _ {1}}$		[∞]	${displaystyle left [{egin {smallmatrix} 2 & -2 -2 & 2end {smallmatrix}} ight]}$	0
Гиперболический (детерминант≤0)
∞			[∞]	${displaystyle left [{egin {smallmatrix} 2 & -2 -2 & 2end {smallmatrix}} ight]}$	0
∞			[iπ / λ]	${displaystyle left [{egin {smallmatrix} 2 & -2cosh (2lambda) - 2cosh (2lambda) & 2end {smallmatrix}} ight]}$	${displaystyle -4sinh ^ {2} (2lambda) leq 0}$

Геометрические визуализации

Диаграмму Кокстера – Дынкина можно рассматривать как графическое описание фундаментальная область зеркал. Зеркало представляет собой гиперплоскость в заданном сферическом, евклидовом или гиперболическом пространстве. (В 2D-пространстве зеркало - это линия, а в 3D-пространстве - это плоскость).

Эти визуализации показывают фундаментальные области для двумерных и трехмерных евклидовых групп и двумерных сферических групп. Для каждого из них диаграмма Кокстера может быть выведена путем идентификации зеркал гиперплоскости и маркировки их связности, игнорируя двугранные углы 90 градусов (порядок 2).

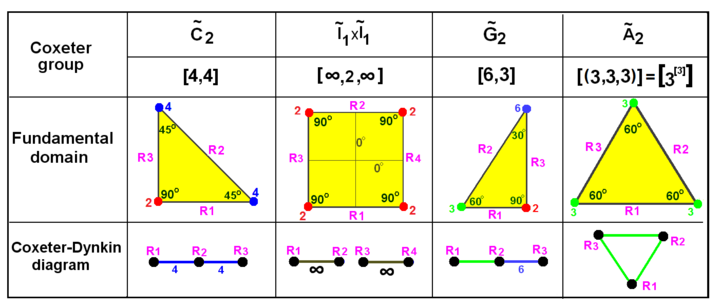Группы Кокстера на евклидовой плоскости с эквивалентными диаграммами. Отражения помечены как узлы графа р1, р2 и т. Д. И раскрашены в порядке их отражения. Отражения под углом 90 градусов неактивны и поэтому не отображаются на диаграмме. Параллельные зеркала соединяются ветвью с обозначением ∞. Призматическая группа ${displaystyle {ilde {I}} _ {1}}$ Икс ${displaystyle {ilde {I}} _ {1}}$ отображается как удвоение ${displaystyle {ilde {C}} _ {2}}$ , но также могут быть созданы в виде прямоугольных областей путем удвоения ${displaystyle {ilde {G}} _ {2}}$ треугольники. В ${displaystyle {ilde {A}} _ {2}}$ это удвоение ${displaystyle {ilde {G}} _ {2}}$ треугольник.
Многие группы Кокстера в гиперболическая плоскость можно продолжить с евклидовых случаев как серию гиперболических решений.
Группы Кокстера в трехмерном пространстве с диаграммами. Зеркала (грани треугольника) помечены противоположной вершиной 0..3. Ветки раскрашены в порядке их отражения. ${displaystyle {ilde {C}} _ {3}}$ заполняет 1/48 куба. ${displaystyle {ilde {B}} _ {3}}$ заполняет 1/24 куба. ${displaystyle {ilde {A}} _ {3}}$ заполняет 1/12 куба.	Группы Кокстера на сфере с эквивалентными диаграммами. Одна фундаментальная область обведена желтым. Вершины домена (и ветви графа) окрашены в соответствии с порядком их отражения.

Конечные группы Кокстера

Смотрите также семейства многогранников для таблицы однородных многогранников конечных узлов, связанных с этими группами.

Для одних и тех же групп даны три разных символа - буква / цифра, набор чисел в скобках и диаграмма Кокстера.
Раздвоенный D_п группы половина или же чередовались версия обычного C_п группы.
Раздвоенный D_п и E_п группы также помечаются надстрочной формой [3^а,б,c] куда а,б,c - количество сегментов в каждой из трех ветвей.

Связные конечные диаграммы Кокстера-Дынкина (ранги с 1 по 9)
Классифицировать	Простые группы Ли			Исключительные группы Ли
Классифицировать	${displaystyle {A} _ {1+}}$	${displaystyle {B} _ {2+}}$	${displaystyle {D} _ {2+}}$	${displaystyle {E} _ {3-8}}$	${displaystyle {F} _ {3-4}}$	${displaystyle {G} _ {2}}$	${displaystyle {H} _ {2-4}}$	${displaystyle {I} _ {2} (p)}$
1	А₁=[ ]
2	А₂=[3]	B₂=[4]	D₂= А₁А₁			грамм₂=[6]	ЧАС₂=[5]	я₂[п]
3	А₃=[3²]	B₃=[3,4]	D₃= А₃	E₃= А₂А₁	F₃= B₃		ЧАС₃
4	А₄=[3³]	B₄=[3²,4]	D₄=[3^1,1,1]	E₄= А₄	F₄		ЧАС₄
5	А₅=[3⁴]	B₅=[3³,4]	D₅=[3^2,1,1]	E₅= D₅
6	А₆=[3⁵]	B₆=[3⁴,4]	D₆=[3^3,1,1]	E₆=[3^2,2,1]
7	А₇=[3⁶]	B₇=[3⁵,4]	D₇=[3^4,1,1]	E₇=[3^3,2,1]
8	А₈=[3⁷]	B₈=[3⁶,4]	D₈=[3^5,1,1]	E₈=[3^4,2,1]
9	А₉=[3⁸]	B₉=[3⁷,4]	D₉=[3^6,1,1]
10+	..	..	..	..

Приложение с однородными многогранниками

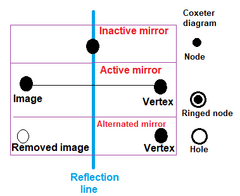При построении однородных многогранников узлы помечаются как активный кольцом, если образующая точка находится за пределами зеркала, создавая новый край между образующей точкой и ее зеркальным отображением. Узел без кольца представляет собой неактивный зеркало, которое не генерирует новых точек. Кольцо без узла называется дыра.	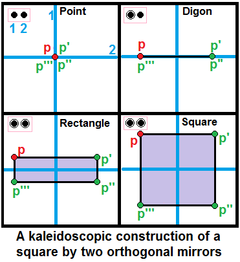Два ортогональных зеркала можно использовать для создания квадрата, , видно здесь с красной точкой генератора и 3 виртуальными копиями через зеркала. В этом ортогональном случае генератор должен находиться вне обоих зеркал, чтобы создать интерьер. Разметка кольца предполагает, что активные кольца имеют генераторы на одинаковом расстоянии от всех зеркал, в то время как прямоугольник также может представлять собой неоднородное решение.

Диаграммы Кокстера – Дынкина позволяют явно перечислить почти все классы равномерный многогранник и однородная мозаика. Каждый однородный многогранник с чистой отражательной симметрией (все, кроме нескольких частных случаев, имеют чистую отражательную симметрию) может быть представлен диаграммой Кокстера – Дынкина с перестановками наценки. Каждый однородный многогранник может быть сгенерирован с использованием таких зеркал и одной точки генератора: зеркальные изображения создают новые точки как отражения, затем многогранник края можно определить между точками и точкой зеркального отображения. Лица генерируются повторным отражением кромки, в конечном итоге оборачивающейся вокруг исходного генератора; окончательная форма, как и любые грани более высокого измерения, аналогично создаются отражением лица, ограничивающим область.

Чтобы указать генерирующую вершину, один или несколько узлов помечаются кольцами, что означает, что вершина нет на зеркале (ах), представленном окольцованным узлом (ами). (Если отмечены два или более зеркала, вершина равноудалена от них.) Зеркало - это активный (создает отражения) только по отношению к точкам не на нем. Для представления многогранника диаграмме нужен хотя бы один активный узел. Несвязанная диаграмма (подгруппы, разделенные ветвями второго порядка или ортогональными зеркалами) требует по крайней мере одного активного узла в каждом подграфе.

Все правильные многогранники, представлена Символ Шлефли { $п, q, р, ...$ }, могут иметь свои фундаментальные области представлен набором п зеркала с соответствующей диаграммой Кокстера-Дынкина линии узлов и ветвей, помеченных $п, q, р, ...,$ с первым узлом окольцованы.

Равномерные многогранники с одним кольцом соответствуют образующим в углах симплекса фундаментальной области. Два кольца соответствуют краям симплекса и имеют степень свободы, причем только средняя точка является однородным решением для равных длин ребер. В целом k- точки генератора колец включены (к-1)-грани симплекса, и если все узлы окольцованы, образующая точка находится внутри симплекса.

Частный случай однородных многогранников с неотражающей симметрией представлен вторичной разметкой, в которой удаляется центральная точка кольцевого узла (называемая дыра). Эти формы чередования^{[требуется разъяснение ]} многогранников с отражающей симметрией, подразумевая, что альтернативные узлы удалены^{[требуется разъяснение ]}. Полученный многогранник будет иметь подсимметрию исходного Группа Кокстера. Усеченное чередование называется пренебрежительно.

Один узел представляет собой одно зеркало. Это называется группой A₁. Если обведено, это создает отрезок перпендикулярно зеркалу, обозначенному как {}.
Два неподключенных узла представляют собой два перпендикуляр зеркала. Если оба узла окольцованы, прямоугольник могут быть созданы, или квадрат если точка находится на одинаковом расстоянии от обоих зеркал.
Два узла прикреплены по заказу-п филиал может создать п-угольник если точка находится на одном зеркале, а на 2п-угольник, если точка не на обоих зеркалах. Это формирует я₁(п) группа.
Два параллельных зеркала могут представлять собой бесконечный многоугольник I.₁(∞) группа, также называемая Ĩ₁.
Три зеркала в треугольнике образуют изображения, видимые в традиционном калейдоскоп и может быть представлен тремя узлами, соединенными в треугольник. В повторяющихся примерах ветви будут обозначены как (3 3 3), (2 4 4), (2 3 6), хотя последние два могут быть нарисованы в виде линии (с 2 ветви игнорируются). Это сгенерирует однородные мозаики.
Три зеркала могут создать равномерные многогранники; включая рациональные числа дает набор Треугольники Шварца.
Три зеркала, одно из которых перпендикулярно двум другим, могут образовывать однородные призмы.

Внутри общего треугольника имеется 7 отражающих однородных конструкций, основанных на 7 положениях топологического генератора в основной области. Каждое активное зеркало формирует край, два активных зеркала имеют генераторы на сторонах домена, а три активных зеркала имеют генератор внутри. Одна или две степени свободы могут быть решены для уникального положения для равных длин ребер результирующего многогранника или мозаики.	Пример 7 генераторы на октаэдрическая симметрия, фундаментальный доменный треугольник (4 3 2) с 8-м поколением курноса чередование

Двойники однородных многогранников иногда помечаются перпендикулярной косой чертой, заменяющей кольцевые узлы, и косой чертой для узловых отверстий курносых. Например, представляет прямоугольник (как два активных ортогональных зеркала), и представляет свою двойной многоугольник, то ромб.

Примеры многогранников и мозаик

Например, B₃ Группа Кокстера есть схема: . Это также называется октаэдрическая симметрия.

Есть 7 выпуклых равномерные многогранники которая может быть построена из этой группы симметрии и 3 из ее чередование подсимметрии, каждая из которых имеет однозначно размеченную диаграмму Кокстера – Дынкина. В Символ Wythoff представляет собой частный случай диаграммы Кокстера для графов ранга 3, с указанием всех трех порядков ветвления, а не подавления ветвей порядка 2. Символ Wythoff может обрабатывать пренебрежительно форма, но не общие чередования без всех узлов окольцованы.

Однородные октаэдрические многогранники
Симметрия: [4,3], (*432)							[4,3]⁺ (432)	[1⁺,4,3] = [3,3] (*332)		[3⁺,4] (3*2)
{4,3}	т {4,3}	г {4,3} г {3^1,1}	т {3,4} т {3^1,1}	{3,4} {3^1,1}	рр {4,3} s₂{3,4}	tr {4,3}	sr {4,3}	ч {4,3} {3,3}	час₂{4,3} т {3,3}	с {3,4} с {3^1,1}

		=	=	=				= или же	= или же	=

Двойники к однородным многогранникам
V4³	V3.8²	V (3,4)²	V4.6²	V3⁴	V3.4³	V4.6.8	V3⁴.4	V3³	V3.6²	V3⁵

Такие же конструкции можно сделать на дизъюнктивных (ортогональных) группах Кокстера, подобных равномерной призмы, и более отчетливо его можно рассматривать как мозаику дигедры и осоэдры на сфере, как это семейство [6] × [] или [6,2]:

Однородные шестиугольные двугранные сферические многогранники
Симметрия: [6,2], (*622)							[6,2]⁺, (622)	[6,2⁺], (2*3)


{6,2}	т {6,2}	г {6,2}	т {2,6}	{2,6}	rr {6,2}	tr {6,2}	sr {6,2}	с {2,6}
Двойники к униформе

V6²	V12²	V6²	V4.4.6	V2⁶	V4.4.6	V4.4.12	V3.3.3.6	V3.3.3.3

Для сравнения, [6,3], семейство создает параллельный набор из 7 однородных мозаик евклидовой плоскости и их двойственных мозаик. Снова есть 3 чередования и некоторая полусимметричная версия.

Однородные шестиугольные / треугольные мозаики [ v т е ]
Симметрия: [6,3], (*632)							[6,3]⁺ (632)	[6,3⁺] (3*3)
{6,3}	т {6,3}	г {6,3}	т {3,6}	{3,6}	рр {6,3}	tr {6,3}	sr {6,3}	с {3,6}


6³	3.12²	(3.6)²	6.6.6	3⁶	3.4.6.4	4.6.12	3.3.3.3.6	3.3.3.3.3.3
Униформа двойников

V6³	V3.12²	В (3,6)²	V6³	V3⁶	V3.4.6.4	V.4.6.12	V3⁴.6	V3⁶

В гиперболической плоскости [7,3], семейство производит параллельный набор однородных мозаик и их двойственных мозаик. Есть только 1 чередование (пренебрежительно ), поскольку все порядки ветвлений нечетные. Многие другие гиперболические семейства однородных мозаик можно увидеть на равномерные мозаики в гиперболической плоскости.

Равномерная семиугольная / треугольная мозаика [ v т е ]
Симметрия: [7,3], (*732)							[7,3]⁺, (732)


{7,3}	т {7,3}	г {7,3}	т {3,7}	{3,7}	рр {7,3}	tr {7,3}	sr {7,3}
Униформа двойников


V7³	V3.14.14	V3.7.3.7	V6.6.7	V3⁷	V3.4.7.4	V4.6.14	V3.3.3.3.7

Аффинные группы Кокстера

Семейства выпуклых равномерных евклидовых мозаик определяются аффинные группы Кокстера. Эти группы идентичны конечным группам с включением одного добавленного узла. В названиях букв они обозначаются одной и той же буквой со знаком «~» над буквой. Индекс относится к конечной группе, поэтому ранг равен индексу плюс 1. (Эрнст Витт символы для аффинных групп представлены как также)

${displaystyle {ilde {A}} _ {n-1}}$ : диаграммы этого типа являются циклами. (Также P_п)
${displaystyle {ilde {C}} _ {n-1}}$ связан с гиперкуб обычная тесселяция { $4, 3, ...., 4$ } семья. (Также R_п)
${displaystyle {ilde {B}} _ {n-1}}$ связаны с C одним удаленным зеркалом. (Также S_п)
${displaystyle {ilde {D}} _ {n-1}}$ связаны с C двумя удаленными зеркалами. (Также Q_п)
${displaystyle {ilde {E}} _ {6}}$ , ${displaystyle {ilde {E}} _ {7}}$ , ${displaystyle {ilde {E}} _ {8}}$ . (Также T₇, Т₈, Т₉)
${displaystyle {ilde {F}} _ {4}}$ образует обычную мозаику {3,4,3,3}. (Также U₅)
${displaystyle {ilde {G}} _ {2}}$ образует 30-60-90 фундаментальных областей треугольника. (Также V₃)
${displaystyle {ilde {I}} _ {1}}$ это два параллельных зеркала. знак равно ${displaystyle {ilde {A}} _ {1}}$ = ${displaystyle {ilde {C}} _ {1}}$ ) (Также W₂)

Составные группы также можно определить как ортогональные проекты. Наиболее частое использование ${displaystyle {ilde {A}} _ {1}}$ , подобно ${displaystyle {ilde {A}} _ {1} ^ {2}}$ , представляет квадрат или прямоугольник шахматная доска области на евклидовой плоскости. И ${displaystyle {ilde {A}} _ {1} {ilde {G}} _ {2}}$ представляет треугольная призма фундаментальные области в трехмерном евклидовом пространстве.

Аффинные графы Кокстера до (от 2 до 10 узлов)
Классифицировать	${displaystyle {ilde {A}} _ {1+}}$ (П₂₊)	${displaystyle {ilde {B}} _ {3+}}$ (S₄₊)	${displaystyle {ilde {C}} _ {1+}}$ (Р₂₊)	${displaystyle {ilde {D}} _ {4+}}$ (Q₅₊)	${displaystyle {ilde {E}} _ {n}}$ (Т_{п + 1}) / ${displaystyle {ilde {F}} _ {4}}$ (U₅) / ${displaystyle {ilde {G}} _ {2}}$ (V₃)
2	${displaystyle {ilde {A}} _ {1}}$ =[∞]		${displaystyle {ilde {C}} _ {1}}$ =[∞]
3	${displaystyle {ilde {A}} _ {2}}$ =[3^[3]] *		${displaystyle {ilde {C}} _ {2}}$ =[4,4] *		${displaystyle {ilde {G}} _ {2}}$ =[6,3] *
4	${displaystyle {ilde {A}} _ {3}}$ =[3^[4]] *	${displaystyle {ilde {B}} _ {3}}$ =[4,3^1,1] *	${displaystyle {ilde {C}} _ {3}}$ =[4,3,4] *	${displaystyle {ilde {D}} _ {3}}$ =[3^1,1,3⁻¹,3^1,1] = ${displaystyle {ilde {A}} _ {3}}$
5	${displaystyle {ilde {A}} _ {4}}$ =[3^[5]] *	${displaystyle {ilde {B}} _ {4}}$ =[4,3,3^1,1] *	${displaystyle {ilde {C}} _ {4}}$ =[4,3²,4] *	${displaystyle {ilde {D}} _ {4}}$ =[3^1,1,1,1] *	${displaystyle {ilde {F}} _ {4}}$ =[3,4,3,3] *
6	${displaystyle {ilde {A}} _ {5}}$ =[3^[6]] *	${displaystyle {ilde {B}} _ {5}}$ =[4,3²,3^1,1] *	${displaystyle {ilde {C}} _ {5}}$ =[4,3³,4] *	${displaystyle {ilde {D}} _ {5}}$ =[3^1,1,3,3^1,1] *
7	${displaystyle {ilde {A}} _ {6}}$ =[3^[7]] *	${displaystyle {ilde {B}} _ {6}}$ =[4,3³,3^1,1]	${displaystyle {ilde {C}} _ {6}}$ =[4,3⁴,4]	${displaystyle {ilde {D}} _ {6}}$ =[3^1,1,3²,3^1,1]	${displaystyle {ilde {E}} _ {6}}$ =[3^2,2,2]
8	${displaystyle {ilde {A}} _ {7}}$ =[3^[8]] *	${displaystyle {ilde {B}} _ {7}}$ =[4,3⁴,3^1,1] *	${displaystyle {ilde {C}} _ {7}}$ =[4,3⁵,4]	${displaystyle {ilde {D}} _ {7}}$ =[3^1,1,3³,3^1,1] *	${displaystyle {ilde {E}} _ {7}}$ =[3^3,3,1] *
9	${displaystyle {ilde {A}} _ {8}}$ =[3^[9]] *	${displaystyle {ilde {B}} _ {8}}$ =[4,3⁵,3^1,1]	${displaystyle {ilde {C}} _ {8}}$ =[4,3⁶,4]	${displaystyle {ilde {D}} _ {8}}$ =[3^1,1,3⁴,3^1,1]	${displaystyle {ilde {E}} _ {8}}$ =[3^5,2,1] *
10	${displaystyle {ilde {A}} _ {9}}$ =[3^[10]] *	${displaystyle {ilde {B}} _ {9}}$ =[4,3⁶,3^1,1]	${displaystyle {ilde {C}} _ {9}}$ =[4,3⁷,4]	${displaystyle {ilde {D}} _ {9}}$ =[3^1,1,3⁵,3^1,1]
11	...	...	...	...

Гиперболические группы Кокстера

Есть много бесконечных гиперболических Группы Кокстера. Гиперболические группы классифицируются как компактные или нет, причем компактные группы имеют ограниченные фундаментальные области. Компактные симплексные гиперболические группы (Симплексы Ланнера) существуют как ранги 3–5. Паракомпактные симплексные группы (Кошульские симплексы) существуют до 10 ранга. Гиперкомпактный (Многогранники Винберга) группы были изучены, но не полностью определены. В 2006 году Оллкок доказал, что существует бесконечно много компактных многогранников Винберга размерности до 6 и бесконечно много многогранников Винберга конечного объема размерности до 19,^[4] поэтому полное перечисление невозможно. Все эти фундаментальные отражающие области, как симплексы, так и несимплексы, часто называют Coxeter многогранники или иногда менее точно Coxeter многогранники.

Гиперболические группы в H²

Модель диска Пуанкаре фундаментальной области треугольники
Пример прямоугольных треугольников [p, q]
[3,7]	[3,8]	[3,9]	[3,∞]
[4,5]	[4,6]	[4,7]	[4,8]	[∞,4]
[5,5]	[5,6]	[5,7]	[6,6]	[∞,∞]
Пример общих треугольников [(p, q, r)]
[(3,3,4)]	[(3,3,5)]	[(3,3,6)]	[(3,3,7)]	[(3,3,∞)]
[(3,4,4)]	[(3,6,6)]	[(3,∞,∞)]	[(6,6,6)]	[(∞,∞,∞)]

Двумерный гиперболический группы треугольников существуют как диаграммы Кокстера ранга 3, определенные треугольником (p q r) для:

{displaystyle {frac {1} {p}} + {frac {1} {q}} + {frac {1} {r}} <1.}

Существует бесконечно много компактных треугольных гиперболических групп Кокстера, включая линейные и треугольные графы. Линейные графики существуют для прямоугольных треугольников (с r = 2).^[5]

Компактные гиперболические группы Кокстера

Линейный

Циклический

∞ [p, q],

:
2 (p + q)

...

...

...

∞ [(p, q, r)],

: p + q + r> 9

			...

Паракомпактные группы Кокстера ранга 3 существуют как пределы компактных.

Линейные графики	Циклические графы
[p, ∞] [∞,∞]	[(p, q, ∞)] [(p, ∞, ∞)] [(∞,∞,∞)]

Группа арифметических треугольников

Гиперболический группы треугольников которые также арифметические группы образуют конечное подмножество. Путем компьютерного поиска полный список был определен Кисао Такеучи в его статье 1977 г. Группы арифметических треугольников.^[6] Всего 85, компактных 76 и паракомпактных 9.

Правые треугольники (p q 2)	Общие треугольники (p q r)
Компактные группы: (76) , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , Паракомпактные прямоугольные треугольники: (4) , , ,	Общие треугольники: (39) , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , Паракомпактные общие треугольники: (5) , , , ,
(2 3 7), (2 3 8), (2 3 9), (2 3 10), (2 3 11), (2 3 12), (2 3 14), (2 3 16), (2 3 18), (2 3 24), (2 3 30) (2 4 5), (2 4 6), (2 4 7), (2 4 8), (2 4 10), (2 4 12), (2 4 18), (2 5 5), (2 5 6), (2 5 8), (2 5 10), (2 5 20), (2 5 30) (2 6 6), (2 6 8), (2 6 12) (2 7 7), (2 7 14), (2 8 8), (2 8 16), (2 9 18) (2 10 10) (2 12 12) (2 12 24), (2 15 30), (2 18 18) (2 3 ∞) (2,4 ∞) (2,6 ∞) (2 ∞ ∞)	(3 3 4), (3 3 5), (3 3 6), (3 3 7), (3 3 8), (3 3 9), (3 3 12), (3 3 15) (3 4 4), (3 4 6), (3 4 12), (3 5 5), (3 6 6), (3 6 18), (3 8 8), (3 8 24), (3 10 30), (3 12 12) (4 4 4), (4 4 5), (4 4 6), (4 4 9), (4 5 5), (4 6 6), (4 8 8), (4 16 16) (5 5 5), (5 5 10), (5 5 15), (5 10 10) (6 6 6), (6 12 12), (6 24 24) (7 7 7) (8 8 8) (9 9 9) (9 18 18) (12 12 12) (15 15 15) (3,3 ∞) (3 ∞ ∞) (4,4 ∞) (6 6 ∞) (∞ ∞ ∞)

Гиперболические многоугольники Кокстера над треугольниками

Фундаментальные области четырехугольных групп
Домены с идеальными вершинами
или же [∞,3,∞] [iπ / λ₁, 3, iπ / λ₂] (*3222)	или же [((3,∞,3)),∞] [((3, iπ / λ₁, 3)), iπ / λ₂] (*3322)	или же [(3,∞)^[2]] [(3, iπ / λ₁, 3, iπ / λ₂)] (*3232)	или же [(4,∞)^[2]] [(4, iπ / λ₁, 4, iπ / λ₂)] (*4242)	(*3333)
[iπ / λ₁, ∞, iπ / λ₂] (*∞222)	(*∞∞22)	[(iπ / λ₁, ∞, iπ / λ₂,∞)] (*2∞2∞)	(*∞∞∞∞)	(*4444)

Другой H² гиперболические калейдоскопы могут быть построены из многоугольников более высокого порядка. Нравиться группы треугольников эти калейдоскопы можно идентифицировать по циклической последовательности порядков зеркального пересечения вокруг фундаментальной области, как (a b c d ...), или, что то же самое, в орбифолдная запись в качестве *abcd.... Диаграммы Кокстера-Дынкина для этих полигональных калейдоскопов можно рассматривать как вырожденные (n-1) -симплекс фундаментальные области с циклом ветвей порядка a, b, c ..., а оставшиеся n * (n-3) / 2 ветвей помечены как бесконечные (∞), представляющие непересекающиеся зеркала. Единственный негиперболический пример - это четыре зеркала евклидовой симметрии в квадрат или прямоугольник как , [∞, 2, ∞] (орбифолд * 2222). Другое представление ветви для непересекающихся зеркал: Винберг дает бесконечные ветви в виде пунктирных или пунктирных линий, поэтому эту диаграмму можно представить как , с подавленными по периметру четырьмя ветвями порядка 2.

Например, четырехугольная область (a b c d) будет иметь две ветви бесконечного порядка, соединяющие ультрапараллельные зеркала. Самый маленький гиперболический пример: , [∞, 3, ∞] или [iπ / λ₁, 3, iπ / λ₂] (орбифолд * 3222), где (λ₁, λ₂) - расстояние между ультрапараллельными зеркалами. Альтернативное выражение: , с подавленными по периметру тремя ветвями порядка 2. Аналогично (2 3 2 3) (орбифолд * 3232) можно представить в виде и (3 3 3 3), (орбифолд * 3333) можно представить в виде полного графа .

Наивысшая четырехугольная область (∞ ∞ ∞ ∞) представляет собой бесконечный квадрат, представленный полным четырехгранный граф с 4 ветвями периметра как идеальные вершины и двумя диагональными ветвями как бесконечность (показаны пунктирными линиями) для ультрапараллельный зеркала: .

Компактные (симплексные группы Ланнера)

Компактные гиперболические группы называются группами Ланнера по названию Фольке Ланнер кто впервые изучил их в 1950 году.^[7] Они существуют только как графики ранга 4 и 5. Кокстер изучал линейные гиперболические группы кокстера в своей статье 1954 года. Обычные соты в гиперболическом пространстве,^[8] который включал два рациональных решения в гиперболическом 4-пространстве: [5/2,5,3,3] = и [5,5 / 2,5,3] = .

4–5 ранги.

Фундаментальная область любой из двух бифуркационных групп, [5,3^1,1] и [5,3,3^1,1], вдвое больше, чем у соответствующей линейной группы, [5,3,4] и [5,3,3,4] соответственно. Названия букв даются Джонсон как расширенный Символы Витта.^[9]

Компактные гиперболические группы Кокстера
Измерение ЧАС^d	Классифицировать	Общее количество	Линейный	Раздвоение	Циклический
ЧАС³	4	9	3: ${displaystyle {overline {BH}} _ {3}}$ = [4,3,5]: ${displaystyle {overline {K}} _ {3}}$ = [5,3,5]: ${displaystyle {overline {J}} _ {3}}$ = [3,5,3]:	${displaystyle {overline {DH}} _ {3}}$ = [5,3^1,1]:	${displaystyle {widehat {AB}} _ {3}}$ = [(3³,4)]: ${displaystyle {widehat {AH}} _ {3}}$ = [(3³,5)]: ${displaystyle {widehat {BB}} _ {3}}$ = [(3,4)^[2]]: ${displaystyle {widehat {BH}} _ {3}}$ = [(3,4,3,5)]: ${displaystyle {widehat {HH}} _ {3}}$ = [(3,5)^[2]]:
ЧАС⁴	5	5	3: ${displaystyle {overline {H}} _ {4}}$ = [3³,5]: ${displaystyle {overline {BH}} _ {4}}$ = [4,3,3,5]: ${displaystyle {overline {K}} _ {4}}$ = [5,3,3,5]:	${displaystyle {overline {DH}} _ {4}}$ = [5,3,3^1,1]:	${displaystyle {widehat {AF}} _ {4}}$ = [(3⁴,4)]:

Паракомпакт (симплексные группы Кошуля)

Пример апейрогональная мозаика порядка 3, {∞, 3} с одним зеленым апейрогон и его ограниченный орицикл

Паракомпактные (также называемые некомпактными) гиперболические группы Кокстера содержат аффинные подгруппы и имеют асимптотические симплексные фундаментальные области. Высшая паракомпактная гиперболическая группа Кокстера имеет 10 ранг. Эти группы названы в честь французского математика. Жан-Луи Кошул.^[10] Их также называют квазиланнеровскими группами, продолжающими компактные группы Ланнера. Полный список был составлен М. Чейном путем компьютерного поиска и опубликован в 1969 году.^[11]

По Винбергу, все 72 компактных и паракомпактных симплекса, кроме восьми, являются арифметическими. Две из неарифметических групп компактны: и . Остальные шесть неарифметических групп все паракомпактны, с пятью трехмерными группами. , , , , и , и одна 5-мерная группа .

Идеальные симплексы

Идеальные фундаментальные области

, [(∞, ∞, ∞)] видно в Модель диска Пуанкаре

Существует 5 гиперболических групп Кокстера, выражающих идеальные симплексы, графы, в которых удаление любого одного узла приводит к аффинной группе Кокстера. Таким образом, все вершины этого идеального симплекса находятся на бесконечности.^[12]

Классифицировать	Идеальная группа	Аффинные подгруппы
3	[(∞,∞,∞)]	[∞]
4	[4^[4]]	[4,4]
4	[3^[3,3]]	[3^[3]]
4	[(3,6)^[2]]	[3,6]
6	[(3,3,4)^[2]]	[4,3,3,4], [3,4,3,3]	,

4–10 ранги.

Бесконечные евклидовы клетки как шестиугольная черепица, правильно масштабированные, сходятся к единственной идеальной точке на бесконечности, как шестиугольная черепичная сотовая конструкция, {6,3,3}, как показано с этой единственной ячейкой в Модель диска Пуанкаре проекция.

Всего существует 58 паракомпактных гиперболических групп Кокстера с ранга 4 по 10. Все 58 сгруппированы ниже по пяти категориям. Буквенные обозначения даются Джонсон в качестве Расширенные символы Витта, используя PQRSTWUV из аффинных символов Витта и добавляя LMNOXYZ. Эти гиперболические группы обозначаются чертой или шляпкой для циклохимических схем. В скобка из Кокстера является линеаризованным представлением группы Кокстера.

Гиперболические паракомпактные группы
Классифицировать	Общее количество	Группы
4	23	${displaystyle {widehat {BR}} _ {3}}$ = [(3,3,4,4)]: ${displaystyle {widehat {CR}} _ {3}}$ = [(3,4³)]: ${displaystyle {widehat {RR}} _ {3}}$ = [4^[4]]: ${displaystyle {widehat {AV}} _ {3}}$ = [(3³,6)]: ${displaystyle {widehat {BV}} _ {3}}$ = [(3,4,3,6)]: ${displaystyle {widehat {HV}} _ {3}}$ = [(3,5,3,6)]: ${displaystyle {widehat {VV}} _ {3}}$ = [(3,6)^[2]]:	${displaystyle {overline {P}} _ {3}}$ = [3,3^[3]]: ${displaystyle {overline {BP}} _ {3}}$ = [4,3^[3]]: ${displaystyle {overline {HP}} _ {3}}$ = [5,3^[3]]: ${displaystyle {overline {VP}} _ {3}}$ = [6,3^[3]]: ${displaystyle {overline {DV}} _ {3}}$ = [6,3^1,1]: ${displaystyle {overline {O}} _ {3}}$ = [3,4^1,1]: ${displaystyle {overline {M}} _ {3}}$ = [4^1,1,1]:	${displaystyle {overline {R}} _ {3}}$ = [3,4,4]: ${displaystyle {overline {N}} _ {3}}$ = [4³]: ${displaystyle {overline {V}} _ {3}}$ = [3,3,6]: ${displaystyle {overline {BV}} _ {3}}$ = [4,3,6]: ${displaystyle {overline {HV}} _ {3}}$ = [5,3,6]: ${displaystyle {overline {Y}} _ {3}}$ = [3,6,3]: ${displaystyle {overline {Z}} _ {3}}$ = [6,3,6]:	${displaystyle {overline {DP}} _ {3}}$ = [3^[]Икс[]]: ${displaystyle {overline {PP}} _ {3}}$ = [3^[3,3]]:
5	9	${displaystyle {overline {P}} _ {4}}$ = [3,3^[4]]: ${displaystyle {overline {BP}} _ {4}}$ = [4,3^[4]]: ${displaystyle {widehat {FR}} _ {4}}$ = [(3²,4,3,4)]: ${displaystyle {overline {DP}} _ {4}}$ = [3^{[3] х []}]:	${displaystyle {overline {N}} _ {4}}$ = [4,3,((4,2,3))]: ${displaystyle {overline {O}} _ {4}}$ = [3,4,3^1,1]: ${displaystyle {overline {S}} _ {4}}$ = [4,3^2,1]:	${displaystyle {overline {R}} _ {4}}$ = [(3,4)²]:	${displaystyle {overline {M}} _ {4}}$ = [4,3^1,1,1]:
6	12	${displaystyle {overline {P}} _ {5}}$ = [3,3^[5]]: ${displaystyle {widehat {AU}} _ {5}}$ = [(3⁵,4)]: ${displaystyle {widehat {AR}} _ {5}}$ = [(3,3,4)^[2]]:	${displaystyle {overline {S}} _ {5}}$ = [4,3,3^2,1]: ${displaystyle {overline {O}} _ {5}}$ = [3,4,3^1,1]: ${displaystyle {overline {N}} _ {5}}$ = [3,(3,4)^1,1]:	${displaystyle {overline {U}} _ {5}}$ = [3³,4,3]: ${displaystyle {overline {X}} _ {5}}$ = [3,3,4,3,3]: ${displaystyle {overline {R}} _ {5}}$ = [3,4,3,3,4]:	${displaystyle {overline {Q}} _ {5}}$ = [3^2,1,1,1]: ${displaystyle {overline {M}} _ {5}}$ = [4,3,3^1,1,1]: ${displaystyle {overline {L}} _ {5}}$ = [3^1,1,1,1,1]:
7	3	${displaystyle {overline {P}} _ {6}}$ = [3,3^[6]]:	${displaystyle {overline {Q}} _ {6}}$ = [3^1,1,3,3^2,1]:	${displaystyle {overline {S}} _ {6}}$ = [4,3²,3^2,1]:
8	4	${displaystyle {overline {P}} _ {7}}$ = [3,3^[7]]:	${displaystyle {overline {Q}} _ {7}}$ = [3^1,1,3²,3^2,1]:	${displaystyle {overline {S}} _ {7}}$ = [4,3³,3^2,1]:	${displaystyle {overline {T}} _ {7}}$ = [3^3,2,2]:
9	4	${displaystyle {overline {P}} _ {8}}$ = [3,3^[8]]:	${displaystyle {overline {Q}} _ {8}}$ = [3^1,1,3³,3^2,1]:	${displaystyle {overline {S}} _ {8}}$ = [4,3⁴,3^2,1]:	${displaystyle {overline {T}} _ {8}}$ = [3^4,3,1]:
10	4	${displaystyle {overline {P}} _ {9}}$ = [3,3^[9]]:	${displaystyle {overline {Q}} _ {9}}$ = [3^1,1,3⁴,3^2,1]:	${displaystyle {overline {S}} _ {9}}$ = [4,3⁵,3^2,1]:	${displaystyle {overline {T}} _ {9}}$ = [3^6,2,1]:

Подгрупповые отношения паракомпактных гиперболических групп

Эти деревья представляют собой отношения подгрупп паракомпактных гиперболических групп. Индексы подгрупп на каждом подключении выделены красным цветом.^[13] Подгруппы индекса 2 представляют собой зеркальное удаление и фундаментальное удвоение домена. Другие могут быть выведены соизмеримость (целочисленное отношение объемов) для тетраэдрических доменов.

Деревья подгрупп
ЧАС³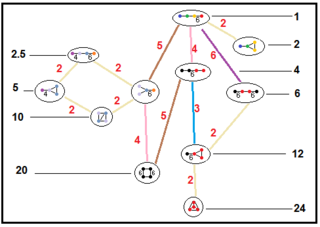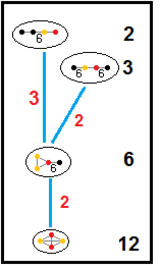
ЧАС⁴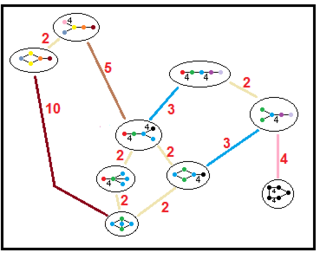
ЧАС⁵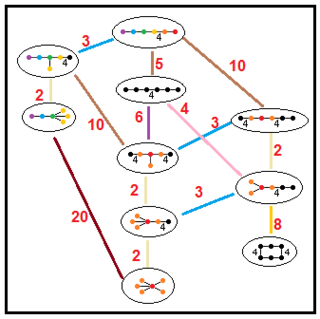

Гиперкомпактные группы Кокстера (многогранники Винберга)

Так же, как гиперболическая плоскость H² имеет нетреугольные многоугольные области, существуют также многомерные отражающие гиперболические области. Эти несимплексные области можно рассматривать как вырожденные симплексы с непересекающимися зеркалами, заданными бесконечным порядком, или на диаграмме Кокстера такие ветви обозначены пунктирными или штриховыми линиями. Эти несложный домены называются Многогранники Винберга, после Эрнест Винберг за его Алгоритм Винберга для нахождения несимплексной фундаментальной области гиперболической группы отражений. Геометрически эти фундаментальные области можно классифицировать как четырехугольники пирамиды, или же призмы или другой многогранники с краями как пересечение двух зеркал, имеющих двугранные углы как π / n для n = 2,3,4 ...

В симплексном домене есть п+1 зеркала для n-мерного пространства. В не симплексных доменах более п+1 зеркала. Список конечен, но не полностью известен. Вместо этого частичные списки были пронумерованы как п+k зеркала для k как 2,3, так и 4.

Гиперкомпактные группы Кокстера в трехмерном пространстве или выше отличаются от двухмерных групп в одном существенном отношении. Два гиперболических n-угольника, имеющие одинаковые углы в одном циклическом порядке, могут иметь разную длину ребер и, как правило, не являются конгруэнтный. В отличие Многогранники Винберга в 3-х измерениях или выше полностью определяются двугранными углами. Этот факт основан на Теорема жесткости Мостова, что две изоморфные группы, порожденные отражениями в H^п для n> = 3 определим конгруэнтные фундаментальные области (многогранники Винберга).

Многогранники Винберга ранга n + 2 для n-мерного пространства

Полный список компактных гиперболических многогранников Винберга ранга п + 2 зеркала для n-мерности были перечислены Ф. Эссельманном в 1996 году.^[14] Частичный список был опубликован в 1974 г. И. М. Каплинской.^[15]

Полный список паракомпактных решений был опубликован П. Тумаркиным в 2003 году с габаритами от 3 до 17.^[16]

Самая маленькая паракомпактная форма в H³ может быть представлен , или [∞, 3,3, ∞], который может быть построен путем зеркального удаления паракомпактной гиперболической группы [3,4,4] как [3,4,1⁺, 4]. Удвоенная фундаментальная область меняется с тетраэдр в четырехугольную пирамиду. Еще пирамиды включают [4,4,1⁺,4] = [∞,4,4,∞], = . Удаление зеркала из некоторых циклических гиперболических графов Кокстера превращается в графы-бабочки: [(3,3,4,1⁺, 4)] = [((3, ∞, 3)), ((3, ∞, 3))] или , [(3,4,4,1⁺, 4)] = [((4, ∞, 3)), ((3, ∞, 4))] или , [(4,4,4,1⁺, 4)] = [((4, ∞, 4)), ((4, ∞, 4))] или .

Другие допустимые паракомпактные графы с фундаментальными областями четырехугольной пирамиды включают:

Измерение	Классифицировать	Графики
ЧАС³	5	, , , , , , , , , , , , , , , , , , , , , , , , , , ,

Другая подгруппа [1⁺,4^1,1,1] = [∞,4,1⁺,4,∞] = [∞^[6]]. = = .^[17]

Многогранники Винберга ранга n + 3 для n-мерного пространства

Существует конечное число вырожденных фундаментальных симплексов, которые могут существовать вплоть до 8-мерных. Полный список компактных многогранников Винберга с рангом п + 3 зеркала для n-мерных измерений были перечислены П. Тумаркиным в 2004 году. Эти группы помечены пунктирными / ломаными линиями для ультрапараллельных ветвей. Полный список некомпактных многогранников Винберга ранга п + 3 зеркала и с одной непростой вершиной для n-мерностей перечислил Майк Робертс.^[18]

Для измерений от 4 до 8 группы Кокстера с 7 по 11 ранги считаются как 44, 16, 3, 1 и 1 соответственно.^[19] Наивысший был обнаружен Бугаенко в 1984 году в размерности 8, ранг 11:^[20]

Размеры	Классифицировать	Случаи	Графики
ЧАС⁴	7	44	...
ЧАС⁵	8	16	..
ЧАС⁶	9	3
ЧАС⁷	10	1
ЧАС⁸	11	1

Многогранники Винберга ранга n + 4 для n-мерного пространства

Существует конечное число вырожденных фундаментальных симплексов, которые существуют до 8-мерного размера. Компактные многогранники Винберга с рангом п + 4 зеркала для n-мерности были исследованы А. Феликсоном и П. Тумаркиным в 2005 году.^[21]

Лоренцевы группы

Регулярные соты с лоренцевыми группами
{3,3,7} рассматривается вне модели шара Пуанкаре	{7,3,3} рассматривается вне модели шара Пуанкаре

Это показывает лоренцевы группы 5-го ранга, упорядоченные как подгруппы из [6,3,3,3] и [6,3,6,3]. Высокосимметричная группа

, [3^[3,3,3]] является подгруппой индекса 120 в [6,3,3,3].

Лоренцевы группы для симплексных областей могут быть определены как графы вне паракомпактных гиперболических форм. Иногда их называют суперидеальными симплексами, и они также связаны с Лоренцева геометрия, названный в честь Хендрик Лоренц в области специальный и общая теория относительности пространство-время, содержащее один (или несколько) своевременный размерные компоненты, скалярные произведения которых отрицательны.^[9] Дэнни Калегари называет это выпуклый кокомпакт Группы Кокстера в n-мерном гиперболическом пространстве.^[22]^[23]

Статья Джорджа Максвелла 1982 г., Сферические упаковки и гиперболические группы отражений, перечисляет конечный список лоренцианов ранга 5-11. Он называет их уровень 2, что означает удаление любой перестановки двух узлов, оставляющей конечный или евклидов граф. Его перечисление полное, но не перечисляет графы, которые являются подгруппой другой. Все ветвящиеся группы Кокстера более высокого порядка ранга 4 лоренцевы и заканчиваются в пределе как полный график 3-симплекс Диаграмма Кокстера-Дынкина с 6 ветвями бесконечного порядка, которые могут быть выражены как [∞^[3,3]]. Ранги 5-11 имеют конечное число групп 186, 66, 36, 13, 10, 8 и 4 лоренцевы группы соответственно.^[24] Статья Х. Чена и Ж.-П. Лаббе, Лоренцианские группы Кокстера и шариковые упаковки Бойда - Максвелла, пересчитал и опубликовал полный список.^[25]

Для самых высоких рангов 8-11 полные списки:

Лоренцевы группы Кокстера
Классифицировать	Общий считать	Группы
4	∞	[3,3,7] ... [∞,∞,∞]: ... [4,3^[3]] ... [∞,∞^[3]]: ... [5,4^1,1] ... [∞^1,1,1]: ... ... [(5,4,3,3)] ... [∞^[4]]: ... ... ... [4^[]×[]] ... [∞^[]×[]]: ... ... [4^[3,3]] ... [∞^[3,3]]
5	186	...[3^[3,3,3]]:...
6	66
7	36	[3^1,1,1,1,1,1]: ...
8	13	[3,3,3^[6]]: [3,3^[6],3]: [3,3^[2+4],3]: [3,3^[1+5],3]: [3^{[] e × [3]}]:	[4,3,3,3^3,1]: [3^1,1,3,3^3,1]: [3,(3,3,4)^1,1]: [3^2,1,3,3^2,1]:		[4,3,3,3^2,2]: [3^1,1,3,3^2,2]:
9	10	[3,3^[3+4],3]: [3,3^[9]]: [3,3^[2+5],3]:	[3^2,1,3²,3^2,1]:	[3^3,1,3³,4]: [3^3,1,3,3,3^1,1]:	[3^3,3,2]: [3^2,2,4]: [3^2,2,3³,4]: [3^2,2,3,3,3^1,1]:
10	8	[3,3^[8],3]: [3,3^[3+5],3]: [3,3^[9]]:	[3^2,1,3³,3^2,1]:	[3^5,3,1]: [3^3,1,3⁴,4]: [3^3,1,3³,3^1,1]:	[3^4,4,1]:
11	4		[3^2,1,3⁴,3^2,1]:	[3^2,1,3⁶,4]: [3^2,1,3⁵,3^1,1]:	[3^7,2,1]:

Очень расширенные диаграммы Кокстера

Одно использование включает очень расширенный определение из прямого Диаграмма Дынкина использование, которое рассматривает аффинные группы как расширенный, гиперболические группы чрезмерно расширенный, а третий узел как очень расширенный простые группы. Эти расширения обычно обозначаются показателем 1,2 или 3. + символы для количества расширенных узлов. Эту расширяющуюся серию можно продолжить назад, последовательно удаляя узлы из одной и той же позиции в графе, хотя процесс останавливается после удаления узла ветвления. В E₈ расширенная семья - наиболее часто показываемый пример, продолжающийся назад от E₃ и вперед на E₁₁.

Процесс расширения может определять ограниченную серию графов Кокстера, которые прогрессируют от конечного к аффинному и от гиперболического к лоренцеву. Определитель матриц Картана определяет, где ряд изменяется от конечного (положительного) до аффинного (ноль), до гиперболического (отрицательного) и заканчивается лоренцевой группой, содержащей по крайней мере одну гиперболическую подгруппу.^[26] Некристалографическая H_п группы образуют расширенную серию, где H₄ расширяется как компактный гиперболик и сверхрасширяется до лоренцевой группы.

Определители матрицы Шлефли по рангу следующие:^[27]

det (A₁^п=[2^п-1]) = 2^п (Конечное для всех n)
det (A_п=[3^п-1]) = n + 1 (конечно для всех n)
det (B_п=[4,3^п-2]) = 2 (Конечное для всех n)
det (D_п=[3^п-3,1,1]) = 4 (Конечное для всех n)

Определители матрицы Шлефли в исключительных рядах:

det (E_п =[3^п-3,2,1]) = 9-n (Конечное для E₃(= А₂А₁), E₄(= А₄), E₅(= D₅), E₆, E₇ и E₈, аффинно в E₉ ( ${displaystyle {ilde {E}} _ {8}}$ ), гиперболический в E₁₀)
det ([3^п-4,3,1]) = 2 (8-n) (Конечное для n = от 4 до 7, аффинное ( ${displaystyle {ilde {E}} _ {7}}$ ) и гиперболической при n = 8.)
det ([3^п-4,2,2]) = 3 (7-n) (Конечное для n = от 4 до 6, аффинное ( ${displaystyle {ilde {E}} _ {6}}$ ) и гиперболической при n = 7.)
det (F_п=[3,4,3^п-3]) = 5-n (Конечное для F₃(= B₃) к F₄, аффинно в F₅ ( ${displaystyle {ilde {F}} _ {4}}$ ), гиперболический в F₆)
det (G_п=[6,3^п-2]) = 3-n (Конечное для грамм₂, аффинно в G₃ ( ${displaystyle {ilde {G}} _ {2}}$ ), гиперболический в G₄)

Меньшая расширенная серия
Конечный	${displaystyle A_ {2}}$	${displaystyle C_ {2}}$	${displaystyle G_ {2}}$	${displaystyle A_ {3}}$	${displaystyle B_ {3}}$	${displaystyle C_ {3}}$	${displaystyle H_ {4}}$
Ранг n	[3^[3],3^п-3]	[4,4,3^п-3]	грамм_п=[6,3^п-2]	[3^[4],3^п-4]	[4,3^{1, н-3}]	[4,3,4,3^п-4]	ЧАС_п=[5,3^п-2]
2	[3] А₂	[4] C₂	[6] грамм₂		[2] А₁²	[4] C₂	[5] ЧАС₂
3	[3^[3]] А₂⁺= ${displaystyle {ilde {A}} _ {2}}$	[4,4] C₂⁺= ${displaystyle {ilde {C}} _ {2}}$	[6,3] грамм₂⁺= ${displaystyle {ilde {G}} _ {2}}$	[3,3] = А₃	[4,3] B₃	[4,3] C₃	[5,3] ЧАС₃
4	[3^[3],3] А₂⁺⁺= ${displaystyle {overline {P}} _ {3}}$	[4,4,3] C₂⁺⁺= ${displaystyle {overline {R}} _ {3}}$	[6,3,3] грамм₂⁺⁺= ${displaystyle {overline {V}} _ {3}}$	[3^[4]] А₃⁺= ${displaystyle {ilde {A}} _ {3}}$	[4,3^1,1] B₃⁺= ${displaystyle {ilde {B}} _ {3}}$	[4,3,4] C₃⁺= ${displaystyle {ilde {C}} _ {3}}$	[5,3,3] ЧАС₄
5	[3^[3],3,3] А₂⁺⁺⁺	[4,4,3,3] C₂⁺⁺⁺	[6,3,3,3] грамм₂⁺⁺⁺	[3^[4],3] А₃⁺⁺= ${displaystyle {overline {P}} _ {4}}$	[4,3^2,1] B₃⁺⁺= ${displaystyle {overline {S}} _ {4}}$	[4,3,4,3] C₃⁺⁺= ${displaystyle {overline {R}} _ {4}}$	[5,3³] ЧАС₅= ${displaystyle {overline {H}} _ {4}}$
6				[3^[4],3,3] А₃⁺⁺⁺	[4,3^3,1] B₃⁺⁺⁺	[4,3,4,3,3] C₃⁺⁺⁺	[5,3⁴] ЧАС₆
Дет (M_п)	3(3-п)	2(3-п)	3-п	4(4-п)	2(4-п)

Средняя расширенная серия
Конечный	${displaystyle A_ {4}}$	${displaystyle B_ {4}}$	${displaystyle C_ {4}}$	${displaystyle D_ {4}}$	${displaystyle F_ {4}}$	${displaystyle A_ {5}}$	${displaystyle B_ {5}}$	${displaystyle D_ {5}}$
Ранг n	[3^[5],3^п-5]	[4,3,3^п-4,1]	[4,3,3,4,3^п-5]	[3^п-4,1,1,1]	[3,4,3^п-3]	[3^[6],3^п-6]	[4,3,3,3^п-5,1]	[3^1,1,3,3^п-5,1]
3		[4,3^−1,1] B₂А₁	[4,3] B₃	[3^−1,1,1,1] А₁³	[3,4] B₃		[4,3,3] C₃
4	[3³] А₄	[4,3,3] B₄	[4,3,3] C₄	[3^0,1,1,1] D₄	[3,4,3] F₄		[4,3,3,3^−1,1] B₃А₁	[3^1,1,3,3^−1,1] А₃А₁
5	[3^[5]] А₄⁺= ${displaystyle {ilde {A}} _ {4}}$	[4,3,3^1,1] B₄⁺= ${displaystyle {ilde {B}} _ {4}}$	[4,3,3,4] C₄⁺= ${displaystyle {ilde {C}} _ {4}}$	[3^1,1,1,1] D₄⁺= ${displaystyle {ilde {D}} _ {4}}$	[3,4,3,3] F₄⁺= ${displaystyle {ilde {F}} _ {4}}$	[3⁴] А₅	[4,3,3,3,3] B₅	[3^1,1,3,3] D₅
6	[3^[5],3] А₄⁺⁺= ${displaystyle {overline {P}} _ {5}}$	[4,3,3^2,1] B₄⁺⁺= ${displaystyle {overline {S}} _ {5}}$	[4,3,3,4,3] C₄⁺⁺= ${displaystyle {overline {R}} _ {5}}$	[3^2,1,1,1] D₄⁺⁺= ${displaystyle {overline {Q}} _ {5}}$	[3,4,3³] F₄⁺⁺= ${displaystyle {overline {U}} _ {5}}$	[3^[6]] А₅⁺= ${displaystyle {ilde {A}} _ {5}}$	[4,3,3,3^1,1] B₅⁺= ${displaystyle {ilde {B}} _ {5}}$	[3^1,1,3,3^1,1] D₅⁺= ${displaystyle {ilde {D}} _ {5}}$
7	[3^[5],3,3] А₄⁺⁺⁺	[4,3,3^3,1] B₄⁺⁺⁺	[4,3,3,4,3,3] C₄⁺⁺⁺	[3^3,1,1,1] D₄⁺⁺⁺	[3,4,3⁴] F₄⁺⁺⁺	[3^[6],3] А₅⁺⁺= ${displaystyle {overline {P}} _ {6}}$	[4,3,3,3^2,1] B₅⁺⁺= ${displaystyle {overline {S}} _ {6}}$	[3^1,1,3,3^2,1] D₅⁺⁺= ${displaystyle {overline {Q}} _ {6}}$
8						[3^[6],3,3] А₅⁺⁺⁺	[4,3,3,3^3,1] B₅⁺⁺⁺	[3^1,1,3,3^3,1] D₅⁺⁺⁺
Дет (M_п)	5(5-п)	2(5-п)		4(5-п)	5-п	6(6-п)	4(6-п)

Некоторые высшие расширенные серии
Конечный	${displaystyle A_ {6}}$	${displaystyle B_ {6}}$	${displaystyle D_ {6}}$	${displaystyle E_ {6}}$	${displaystyle A_ {7}}$	${displaystyle B_ {7}}$	${displaystyle D_ {7}}$	${displaystyle E_ {7}}$	${displaystyle E_ {8}}$
Ранг n	[3^[7],3^п-7]	[4,3³,3^п-6,1]	[3^1,1,3,3,3^п-6,1]	[3^п-5,2,2]	[3^[8],3^п-8]	[4,3⁴,3^п-7,1]	[3^1,1,3,3,3,3^п-7,1]	[3^п-5,3,1]	E_п=[3^п-4,2,1]
3									[3^−1,2,1] E₃= А₂А₁
4				[3^−1,2,2] А₂²				[3^−1,3,1] А₃А₁	[3^0,2,1] E₄= А₄
5		[4,3,3,3,3^−1,1] B₄А₁	[3^1,1,3,3,3^−1,1] D₄А₁	[3^0,2,2] А₅				[3^0,3,1] А₅	[3^1,2,1] E₅= D₅
6	[3⁵] А₆	[4,3⁴] B₆	[3^1,1,3,3,3] D₆	[3^1,2,2] E₆		[4,3,3,3,3,3^−1,1] B₅А₁	[3^1,1,3,3,3,3^−1,1] D₅А₁	[3^1,3,1] D₆	[3^2,2,1] E₆ *
7	[3^[7]] А₆⁺= ${displaystyle {ilde {A}} _ {6}}$	[4,3³,3^1,1] B₆⁺= ${displaystyle {ilde {B}} _ {6}}$	[3^1,1,3,3,3^1,1] D₆⁺= ${displaystyle {ilde {D}} _ {6}}$	[3^2,2,2] E₆⁺= ${displaystyle {ilde {E}} _ {6}}$	[3⁶] А₇	[4,3⁵] B₇	[3^1,1,3,3,3,3^0,1] D₇	[3^2,3,1] E₇ *	[3^3,2,1] E₇ *
8	[3^[7],3] А₆⁺⁺= ${displaystyle {overline {P}} _ {7}}$	[4,3³,3^2,1] B₆⁺⁺= ${displaystyle {overline {S}} _ {7}}$	[3^1,1,3,3,3^2,1] D₆⁺⁺= ${displaystyle {overline {Q}} _ {7}}$	[3^3,2,2] E₆⁺⁺= ${displaystyle {overline {T}} _ {7}}$	[3^[8]] А₇⁺= ${displaystyle {ilde {A}} _ {7}}$ *	[4,3⁴,3^1,1] B₇⁺= ${displaystyle {ilde {B}} _ {7}}$ *	[3^1,1,3,3,3,3^1,1] D₇⁺= ${displaystyle {ilde {D}} _ {7}}$ *	[3^3,3,1] E₇⁺= ${displaystyle {ilde {E}} _ {7}}$ *	[3^4,2,1] E₈ *
9	[3^[7],3,3] А₆⁺⁺⁺	[4,3³,3^3,1] B₆⁺⁺⁺	[3^1,1,3,3,3^3,1] D₆⁺⁺⁺	[3^4,2,2] E₆⁺⁺⁺	[3^[8],3] А₇⁺⁺= ${displaystyle {overline {P}} _ {8}}$ *	[4,3⁴,3^2,1] B₇⁺⁺= ${displaystyle {overline {S}} _ {8}}$ *	[3^1,1,3,3,3,3^2,1] D₇⁺⁺= ${displaystyle {overline {Q}} _ {8}}$ *	[3^4,3,1] E₇⁺⁺= ${displaystyle {overline {T}} _ {8}}$ *	[3^5,2,1] E₉= E₈⁺= ${displaystyle {ilde {E}} _ {8}}$ *
10					[3^[8],3,3] А₇⁺⁺⁺ *	[4,3⁴,3^3,1] B₇⁺⁺⁺ *	[3^1,1,3,3,3,3^3,1] D₇⁺⁺⁺ *	[3^5,3,1] E₇⁺⁺⁺ *	[3^6,2,1] E₁₀= E₈⁺⁺= ${displaystyle {overline {T}} _ {9}}$ *
11									[3^7,2,1] E₁₁= E₈⁺⁺⁺ *
Дет (M_п)	7(7-п)	2(7-п)	4(7-п)	3(7-п)	8(8-п)	2(8-п)	4(8-п)	2(8-п)	9-п

Геометрическое складывание

Конечные и аффинные складки^[28]
φ_А : А_Γ -> А_{Γ '} для конечных типов
Γ	Γ '	Описание складывания	Диаграммы Кокстера – Дынкина
я₂(час )	Γ (h)	Двугранная складка
B_п	А_2n	(Является_п)
B_п	D_{п + 1}, А_2н-1	(А₃, + / - ε)
F₄	E₆	(А₃, ± ε)
ЧАС₄	E₈	(А₄, ± ε)
ЧАС₃	D₆
ЧАС₂	А₄
грамм₂	А₅	(А₅, ± ε)
грамм₂	D₄	(D₄, ± ε)
φ: А_Γ⁺ -> А_{Γ '}⁺ для аффинных типов
${displaystyle {ilde {A}} _ {n-1}}$	${displaystyle {ilde {A}} _ {kn-1}}$	Локально тривиально
${displaystyle {ilde {B}} _ {n}}$	${displaystyle {ilde {D}} _ {2n + 1}}$	(Является_п)
${displaystyle {ilde {B}} _ {n}}$	${displaystyle {ilde {D}} _ {n + 1}}$ , ${displaystyle {ilde {D}} _ {2n}}$	(А₃, ± ε)
${displaystyle {ilde {C}} _ {n}}$	${displaystyle {ilde {B}} _ {n + 1}}$ , ${displaystyle {ilde {C}} _ {2n}}$	(А₃, ± ε)
${displaystyle {ilde {C}} _ {n}}$	${displaystyle {ilde {C}} _ {2n + 1}}$	(Является_п)
${displaystyle {ilde {C}} _ {n}}$	${displaystyle {ilde {A}} _ {2n + 1}}$	(Является_п) & (Является₀)
	${displaystyle {ilde {A}} _ {2n}}$	(А₃, ε) & (I, s₀)
	${displaystyle {ilde {A}} _ {2n-1}}$	(А₃, ε) & (A₃, ε ')
${displaystyle {ilde {C}} _ {n}}$	${displaystyle {ilde {D}} _ {n + 2}}$	(А₃, -ε) & (A₃, -ε ')
${displaystyle {ilde {C}} _ {2}}$	${displaystyle {ilde {D}} _ {5}}$	(Является₁)
${displaystyle {ilde {F}} _ {4}}$	${displaystyle {ilde {E}} _ {6}}$ , ${displaystyle {ilde {E}} _ {7}}$	(А₃, ± ε)
${displaystyle {ilde {G}} _ {2}}$	${displaystyle {ilde {D}} _ {6}}$ , ${displaystyle {ilde {E}} _ {7}}$	(А₅, ± ε)
	${displaystyle {ilde {B}} _ {3}}$ , ${displaystyle {ilde {F}} _ {4}}$	(B₃, ± ε)
	${displaystyle {ilde {D}} _ {4}}$ , ${displaystyle {ilde {E}} _ {6}}$	(D₄, ± ε)

Диаграмма Кокстера – Дынкина (конечная, аффинный, или гиперболический), имеющий симметрию (удовлетворяющую одному условию, указанному ниже), можно разделить по симметрии, давая новую, как правило, многократно зашнурованную диаграмму с процессом, называемым «складывание».^[29]^[30]

Например, в D₄ сворачивание в G₂, ребро в G₂ указывает от класса 3 внешних узлов (валентность 1) до класса центрального узла (валентность 3). И E₈ складывается в 2 копии H₄, вторая копия масштабируется на τ.^[31]

Геометрически это соответствует ортогональные проекции из однородные многогранники и мозаики. Примечательно, что любую конечную диаграмму Кокстера – Дынкина с простыми связями можно свернуть в I₂(час), куда час это Число Кокстера, что геометрически соответствует проекции на Самолет Кокстера.

Несколько гиперболических складок

Сложные размышления

Диаграммы Кокстера – Дынкина распространены на сложное пространство, С^п где узлы унитарные отражения с периодом больше 2. Узлы помечаются индексом, который предполагается равным 2 для обычного реального отражения, если оно подавлено. Кокстер записывает комплексную группу p [q] r как диаграмму .^[32]

Одномерный обычный сложный многогранник в ${displaystyle mathbb {C} ^ {1}}$ представлен как , имея п вершины. Его реальное представление - это правильный многоугольник, {п}. Его симметрия _п[] или же , порядок п. А унитарный оператор генератор для рассматривается как вращение в ${displaystyle mathbb {R} ^ {2}}$ на 2π /п радианы против часовой стрелки, а край создается последовательным применением одного унитарного отражения. Генератор унитарного отражения для 1-многогранника с п вершины $е 2π я / п = cos (2π / п) + я грех (2π / п)$ . Когда п = 2, генератор е^πя = –1, то же, что и точечное отражение в реальном самолете.

В более высоком многограннике _п{} или же представляет п-реберный элемент, с 2-гранью, {} или , представляющий собой обычное реальное ребро между двумя вершинами.

Правильные комплексные 1-многогранники
Сложные 1-многогранники, , представленные в Самолет Арганд как правильные многоугольники для п = 2, 3, 4, 5 и 6 с черными вершинами. Центроид п вершины показаны красным цветом. Стороны многоугольников представляют собой одно приложение генератора симметрии, сопоставляя каждую вершину со следующей копией против часовой стрелки. Эти многоугольные стороны не являются краевыми элементами многогранника, так как сложный 1-многогранник не может иметь ребер (часто является сложное ребро) и содержит только вершинные элементы.

12 неприводимых групп Шепарда с их отношениями индексов подгрупп.^[33] Подгруппы индекса 2 связаны удалением реального отражения: _п[2q]₂ --> _п[q]_п, индекс 2. _п[4]_q --> _п[q]_п, индекс q.	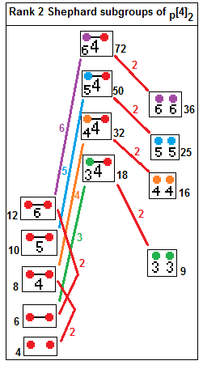_п[4]₂ подгруппы: p = 2,3,4 ... _п[4]₂ --> [п], индекс п _п[4]₂ --> _п[]×_п[], индекс 2

Аа правильные сложные многоугольники в ${displaystyle mathbb {C} ^ {2}}$ , имеет вид _п{q}_р или диаграмма Кокстера . Группа симметрии правильного сложного многоугольника не называется Группа Кокстера, но вместо этого Группа Шепард, тип Комплексная группа отражений. Получатель чего-то _п[q]_р является ${displaystyle 8 / qcdot (1 / p + 2 / q + 1 / r-1) ^ {- 2}}$ .^[34]

Группы шепардов 2-го ранга: ₂[q]₂, _п[4]₂, ₃[3]₃, ₃[6]₂, ₃[4]₃, ₄[3]₄, ₃[8]₂, ₄[6]₂, ₄[4]₃, ₃[5]₃, ₅[3]₅, ₃[10]₂, ₅[6]₂, и ₅[4]₃ или же , , , , , , , , , , , , , порядка 2q, 2п², 24, 48, 72, 96, 144, 192, 288, 360, 600, 1200 и 1800 соответственно.

Группа симметрии _п₁[q]_п₂ представлен двумя образующими R₁, Р₂, где: R₁^п₁ = R₂^п₂ = I. Если q четно, (R₂р₁)^q/2 = (R₁р₂)^q/2. Если q нечетно, (R₂р₁)^{(q-1) / 2}р₂ = (R₁р₂)^(q-1)/2р₁. Когда q странно, п₁=п₂.

В ${displaystyle mathbb {C} ^ {3}}$ группа или [1 1 1]^п определяется 3 унитарными отражениями периода 2 {R₁, Р₂, Р₃}: Р₁² = R₁² = R₃² = (R₁р₂)³ = (R₂р₃)³ = (R₃р₁)³ = (R₁р₂р₃р₁)^п = 1. Период п можно рассматривать как двойное вращение в действительности ${displaystyle mathbb {R} ^ {4}}$ .

Похожий ${displaystyle mathbb {C} ^ {3}}$ группа или [1 1 1]^(п) определяется 3 унитарными отражениями периода 2 {R₁, Р₂, Р₃}: Р₁² = R₁² = R₃² = (R₁р₂)³ = (R₂р₃)³ = (R₃р₁)³ = (R₁р₂р₃р₂)^п = 1.

Смотрите также

дальнейшее чтение

Джеймс Э. Хамфрис, Группы отражений и группы Кокстера, Кембриджские исследования по высшей математике, 29 (1990)
Калейдоскопы: Избранные произведения Х.С.М. Coxeter, под редакцией Ф. Артура Шерка, Питера Макмаллена, Энтони С. Томпсона, Асии Ивика Вайса, публикации Wiley-Interscience, 1995, ISBN 978-0-471-01003-6 [8], Googlebooks [9]
- (Документ 17) Coxeter, Эволюция диаграмм Кокстера-Дынкина, [Nieuw Archief voor Wiskunde 9 (1991) 233-248]
Coxeter, Красота геометрии: двенадцать эссе, Dover Publications, 1999 г., ISBN 978-0-486-40919-1 (Глава 3: Конструкция Витхоффа для однородных многогранников)
Coxeter, Правильные многогранники (1963), компания Macmillan
- Правильные многогранники, Третье издание, (1973), Дуврское издание, ISBN 0-486-61480-8 (Глава 5: Калейдоскоп и Раздел 11.3 Представление в виде графиков)
H.S.M. Кокстер и У. О. Дж. Мозер. Генераторы и соотношения для дискретных групп 4-е изд., Springer-Verlag. Нью-Йорк. 1980 г.
Норман Джонсон, Геометрии и преобразования, Главы 11,12,13, препринт 2011 г.
Н. В. Джонсон, Р. Келлерхальс, Дж. Г. Рэтклифф, С. Т. Чанц, Размер гиперболического симплекса Кокстера, Transformation Groups 1999, Volume 4, Issue 4, pp 329–353. [10] [11]
Норман У. Джонсон и Азия Ивич Вайс Квадратичные целые числа и группы Кокстера PDF Может. J. Math. Vol. 51 (6), 1999, стр. 1307–1336

внешняя ссылка

Вайсштейн, Эрик В. «Диаграмма Кокстера – Дынкина». MathWorld.
Октябрь 1978 г. - обсуждение истории диаграмм Кокстера. Кокстером и Дынкиным в Торонто, Канада; Евгений Дынкин Сборник математических интервью, Библиотека Корнельского университета.

[1] Холл, Брайан К. (2003), Группы Ли, алгебры Ли и представления: элементарное введение, Спрингер, ISBN 978-0-387-40122-5

[2] Кокстер, Правильные многогранники, (3-е издание, 1973 г.), Дуврское издание, ISBN 0-486-61480-8, П. 7.7. стр. 133, Критерий Шлефли

[3] Ланнер Ф., О комплексах с транзитивными группами автоморфизмов, Medd. Lunds Univ. Мат. Сем. [Комм. Сем. Математика. Univ. Лунд], 11 (1950), 1–71.

[4] Оллкок, Дэниел (11 июля 2006 г.). «Бесконечно много гиперболических групп Кокстера через размерность 19». Геометрия и топология. 10 (2): 737–758. arXiv:0903.0138. Дои:10.2140 / gt.2006.10.737.

[5] Геометрия и топология групп Кокстера., Майкл В. Дэвис, 2008 г. п. 105 Таблица 6.2. Гиперболические диаграммы

[6] Такеучи, Кисао (январь 1977 г.). "ТАКЕУЧИ: Арифметические группы треугольников". Журнал математического общества Японии. Projecteuclid.org. 29 (1): 91–106. Дои:10.2969 / jmsj / 02910091. Получено 2013-07-05.

[7] Фольке Ланнер, О комплексах с транзитивными группами автоморфизмов, Comm. Sém., Math. Univ. Лунд [Medd. Lunds Univ. Мат. Сем.] 11 (1950) [1]

[8] Обычные соты в гиперболическом пространстве, Кокстер, 1954 г.

[johnson2018-9] а ^б Норман Джонсон, Геометрии и преобразования (2018), Глава 13: Гиперболические группы Кокстера, 13.6 Лоренцевы решетки

[10] J. L. Koszul, Лекции о гиперболических группах Кокстера, Университет Нотр-Дам (1967)

[11] M. Chein, Recherche des graphes des matrices de Coxeter hyperboliques d’ordre ≤10, Rev. Française Informat. Recherche Opérationnelle 3 (1969), вып. Сер. Р-3, 3–16 (французский). [2]

[12] Подалгебры гиперболических алгебр Кея-Муди, Рисунок 5.1, стр.13

[13] Johnson, N.W .; Kellerhals, R .; Ratcliffe, J.G .; Чанц, С. (2002). «Классы соизмеримости гиперболических групп Кокстера». Линейная алгебра и ее приложения. 345 (1–3): 119–147. Дои:10.1016 / S0024-3795 (01) 00477-3.

[14] Ф. Эссельманн, Классификация компактных гиперболических d-многогранников Кокстера с d + 2 гранями. Комментарий. Математика. Helvetici 71 (1996), 229–242. [3]

[15] Каплинская И. М., Дискретные группы, порожденные отражениями в гранях симплициальных призм в пространствах Лобачевского. Математика. Примечания, 15 (1974), 88–91. [4]

[16] П. Тумаркин, Гиперболические n-многогранники Кокстера с n + 2 гранями (2003)

[17] Норман У. Джонсон и Асия Ивич Вайс, Квадратичные целые числа и группы Кокстера, Может. J. Math. Vol. 51 (6), 1999, стр. 1307–1336 [5]

[18] [6] Классификация некомпактных многогранников Кокстера с п + 3 Грани и одна непростая вершина

[19] П. Тумаркин, Компактный гиперболический Кокстер (2004)

[20] Бугаенко В. О., Группы автоморфизмов унимодулярных гиперболических квадратичных форм над кольцом Zh√5 + 12 я. Московский унив. Математика. Бык. 39 (1984), 6-14.

[21] Анна Феликсон, Павел Тумаркин, О компактных гиперболических d-многогранниках Кокстера с d + 4 гранями, 2005 [7]

[22] Случайные группы, бриллианты и стекло, Дэнни Калегари из Чикагского университета, 25 июня 2014 г., на конференции Билла Терстона по наследию.

[23] Группы Кокстера и случайные группы, Дэнни Калегари, последняя редакция 4 апреля 2015 г.

[24] Максвелл, Джордж (1982). «Сферические упаковки и гиперболические группы отражений». Журнал алгебры. 79: 78–97. Дои:10.1016/0021-8693(82)90318-0.

[25] Хао Чен, Жан-Филипп Лаббе, Лоренцианские группы Кокстера и упаковки шаров Бойда-Максвелла, https://arxiv.org/abs/1310.8608

[26] Алгебры Каца-Муди в M-теории

[27] Определители Картана – Грама для простых групп Ли, Ву, Альфред К. Т., Американский институт физики, ноябрь 1982 г.

[28] Джон Крисп, 'Инъективные карты между Группы Артина ', Даун по теории групп, Труды специального года по геометрической теории групп, (Австралийский национальный университет, Канберра, Австралия, 1996), Постскриптум В архиве 2005-10-16 на Wayback Machine, pp 13-14, и googlebook, Геометрическая теория групп, стр. 131

[29] Зубер, Жан-Бернар (1998). «Обобщенные диаграммы Дынкина и корневые системы и их складки». Топологическая теория поля: 28–30. arXiv:hep-th / 9707046. Bibcode:1998tftp.conf..453Z. CiteSeerX 10.1.1.54.3122.

[30] Декан, Пьер-Филипп; Бем, Селин; Тварок, Рейдун (2013). «Аффинные расширения некристаллографических групп Кокстера, индуцированные проекцией». Журнал математической физики. 54 (9): 093508. arXiv:1110.5228. Bibcode:2013JMP .... 54i3508D. Дои:10.1063/1.4820441.

[31] Геометрия E8 с точки зрения Клиффорда Успехи в прикладных алгебрах Клиффорда, Март 2017 г., том 27, выпуск 1, стр. 397–421 Пьер-Филипп Декан

[32] Кокстер, Сложные правильные многогранники, второе издание, (1991)

[33] Кокстер, Комплексные правильные многогранники, стр. 177, таблица III

[34] Унитарные группы отражений, стр.87

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

[28]

[29]

[30]

[31]

[32]

[33]

[34]

Диаграмма Кокстера – Дынкина - Coxeter–Dynkin diagram

Содержание

Описание

Матрица Шлефли

Группы Кокстера 2-го ранга

Геометрические визуализации

Конечные группы Кокстера

Приложение с однородными многогранниками

Примеры многогранников и мозаик

Аффинные группы Кокстера

Гиперболические группы Кокстера

Гиперболические группы в H²

Группа арифметических треугольников

Гиперболические многоугольники Кокстера над треугольниками

Компактные (симплексные группы Ланнера)

4–5 ранги.

Паракомпакт (симплексные группы Кошуля)

Идеальные симплексы

4–10 ранги.

Подгрупповые отношения паракомпактных гиперболических групп

Гиперкомпактные группы Кокстера (многогранники Винберга)

Многогранники Винберга ранга n + 2 для n-мерного пространства

Многогранники Винберга ранга n + 3 для n-мерного пространства

Многогранники Винберга ранга n + 4 для n-мерного пространства

Лоренцевы группы

Очень расширенные диаграммы Кокстера

Геометрическое складывание

Сложные размышления

Смотрите также

Рекомендации

дальнейшее чтение

внешняя ссылка

Диаграмма Кокстера – Дынкина - Coxeter–Dynkin diagram

Описание

Матрица Шлефли

Группы Кокстера 2-го ранга

Геометрические визуализации

Конечные группы Кокстера

Приложение с однородными многогранниками

Примеры многогранников и мозаик

Аффинные группы Кокстера

Гиперболические группы Кокстера

Гиперболические группы в H2

Группа арифметических треугольников

Гиперболические многоугольники Кокстера над треугольниками

Компактные (симплексные группы Ланнера)

4–5 ранги.

Паракомпакт (симплексные группы Кошуля)

Идеальные симплексы

4–10 ранги.

Подгрупповые отношения паракомпактных гиперболических групп

Гиперкомпактные группы Кокстера (многогранники Винберга)

Многогранники Винберга ранга n + 2 для n-мерного пространства

Многогранники Винберга ранга n + 3 для n-мерного пространства

Многогранники Винберга ранга n + 4 для n-мерного пространства

Лоренцевы группы

Очень расширенные диаграммы Кокстера

Геометрическое складывание

Сложные размышления

Смотрите также

Рекомендации

дальнейшее чтение

внешняя ссылка

Гиперболические группы в H²