Шестиугольный трапецииэдр - Hexagonal trapezohedron
| Шестиугольный трапецииэдр | |
|---|---|
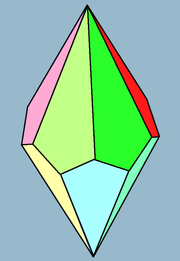 | |
| Тип | трапецоэдры |
| Конвей | dA6 |
| Диаграмма Кокстера | |
| Лица | 12 воздушные змеи |
| Края | 24 |
| Вершины | 14 |
| Конфигурация лица | V6.3.3.3 |
| Группа симметрии | D6d, [2+, 12], (2 * 6), порядок 24 |
| Группа вращения | D6, [2,6]+, (66), порядок 12 |
| Двойной многогранник | шестиугольная антипризма |
| Характеристики | выпуклый, лицо переходный |
В шестиугольник трапецоэдр или же дельтоэдр является четвертым в бесконечной серии однородных по граням многогранников, которые двойственный многогранник к антипризмы. У него двенадцать граней, которые конгруэнтный воздушные змеи.
Вариации
Одна степень свободы внутри D6 симметрия превращает воздушных змеев в конгруэнтные четырехугольники с 3 длинами ребер. В пределе одно ребро каждого четырехугольника достигает нулевой длины, и они становятся бипирамиды.
Хрустальные композиции атомов могут повторяться в пространстве с гексагональными трапециевидными ячейками.[1]
Если воздушные змеи, окружающие две вершины, имеют разную форму, они могут иметь только C6v симметрия, порядок 12. Их можно назвать неравные трапецоэдры. Дуал - это неравный антипризма, с верхним и нижним многоугольниками разного радиуса. Если он скручен и неравен, его симметрия сводится к циклической симметрии, C6 симметрия, порядок 6.
| Тип | Скрученные трапецоэдры (равногранный ) | Неравные трапецоэдры | Неравный и скрученный | |
|---|---|---|---|---|
| Симметрия | D6, (662), [6,2]+, заказ 12 | C6v, (* 66), [6], порядок 12 | C6, (66), [6]+, заказ 6 | |
| Изображение (п=6) |  |  |  |  |
| Сеть |  | 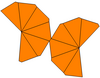 | 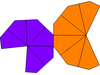 | 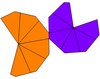 |
Связанные многогранники
| Однородные шестиугольные двугранные сферические многогранники | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Симметрия: [6,2], (*622) | [6,2]+, (622) | [6,2+], (2*3) | ||||||||||||
 |  |  |  |  |  |  | ||||||||
| {6,2} | т {6,2} | г {6,2} | т {2,6} | {2,6} | rr {6,2} | tr {6,2} | sr {6,2} | с {2,6} | ||||||
| Двойники к униформе | ||||||||||||||
 |  |  |  |  |  |  |  |  | ||||||
| V62 | V122 | V62 | V4.4.6 | V26 | V4.4.6 | V4.4.12 | V3.3.3.6 | V3.3.3.3 | ||||||
| Семья п-гональный трапецоэдры | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Изображение многогранника |  |  |  |  |  |  |  |  | ... | Апейрогональный трапецоэдр | |
| Сферическое мозаичное изображение |  |  |  |  |  |  |  |  | Плоское мозаичное изображение | ||
| Конфигурация лица Vп.3.3.3 | V2.3.3.3 | V3.3.3.3 | V4.3.3.3 | V5.3.3.3 | V6.3.3.3 | V7.3.3.3 | V8.3.3.3 | V10.3.3.3 | V12.3.3.3 | ... | V∞.3.3.3 |
внешняя ссылка
- Вайсштейн, Эрик В. «Трапецоэдр». MathWorld.
- Многогранники виртуальной реальности Энциклопедия многогранников
| Этот многогранник -связанная статья является заглушка. Вы можете помочь Википедии расширяя это. |
