Усеченный трапецоэдр - Truncated trapezohedron
| Набор усеченных трапецоэдров | |
|---|---|
 | |
| Обозначения многогранника Конвея | t4dA4 t5dA5 t6dA6 |
| Лица | 2 n-угольники, 2п пятиугольники |
| Края | 6п |
| Вершины | 4п |
| Группа симметрии | Dпd, [2+,2п], (2*п), порядок 4п |
| Группа вращения | Dп, [2, n]+, (22п), порядок 2п |
| Двойной многогранник | гиродлинные дипирамиды |
| Характеристики | выпуклый |
An п-гональный усеченный трапецоэдр это многогранник сформированный п-гональный трапецоэдр с п-угольные пирамиды, усеченные из вершин его двух полярных осей. Если полярные вершины полностью усечены (уменьшены), трапецоэдр становится антипризма.[нужна цитата ]
Вершин существует как 4 п-угольники в четырех параллельных плоскостях с чередующейся ориентацией в середине, создающей пятиугольники.
В правильный додекаэдр является наиболее распространенным многогранником в этом классе, будучи платоническое твердое тело, с 12 конгруэнтными пятиугольными гранями.
А усеченный трапецоэдр имеет все вершины с 3 гранями. Это означает, что двойственные многогранники, множество гиродлинные дипирамиды, имеют все треугольные грани. Например, икосаэдр является двойником додекаэдр.
Формы

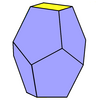

- Треугольный усеченный трапецоэдр (Твердое тело Дюрера ) - 6 пятиугольников, 2 треугольника, двойные гиродлинная треугольная дипирамида
- Усеченный квадратный трапецоэдр - 8 пятиугольников, 2 квадрата, двойные гировидная квадратная дипирамида
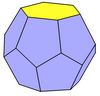
- Усеченный пятиугольный трапецоэдр или же правильный додекаэдр - 12 пятиугольных граней, двойные икосаэдр
- Усеченный шестиугольный трапецоэдр - 12 пятиугольников, 2 шестиугольника, двойные гировидная гексагональная дипирамида
- ...
- Усеченный п-угольный трапецииэдр – 2п пятиугольники, 2 п-угольники, двойные гиродлинные дипирамиды
Смотрите также
внешняя ссылка
- Обозначение Конвея для многогранников Попробуйте: "тпdAп", куда п= 4,5,6 ... пример "t5dA5" - додекаэдр.
| Этот многогранник -связанная статья является заглушка. Вы можете помочь Википедии расширяя это. |
