Додекаэдр - Dodecahedron

Общие додекаэдры

ячас, заказ 120
Обычный-	Малый звездчатый	Большой-	Большой звездчатый
Тчас, заказ 24	Т, заказ 12	Очас, заказ 48	Джонсон (Дж.84)
Пиритоэдр	Тетартоид	Ромбический	Треугольный
D4ч, заказ 16		D3ч, заказ 12
Ромбо-шестиугольный	Ромбо-квадрат	Трапецо-ромбический-	Ромбо-треугольный-

В геометрия, а додекаэдр (Греческий δωδεκάεδρον, из δώδεκα дридека «двенадцать» + ἕδρα Hédra "база", "сиденье" или "лицо") - любое многогранник с двенадцатью плоскими гранями. Самый известный додекаэдр - это правильный додекаэдр с правильными пятиугольниками в качестве лиц, что является Платоново твердое тело. Также есть три правильный звездный додекаэдр, которые строятся как звёздчатые выпуклой формы. Все они имеют икосаэдрическая симметрия, заказ 120.

Некоторые додекаэдры имеют ту же комбинаторную структуру, что и правильный додекаэдр (в терминах графа, образованного его вершинами и ребрами), но их пятиугольные грани не правильные: пиритоэдр, обычная кристаллическая форма в пирит, имеет пиритоэдрическая симметрия, в то время как тетартоид имеет тетраэдрическая симметрия.

В ромбический додекаэдр можно рассматривать как предельный случай пиритоэдра, и он имеет октаэдрическая симметрия. В удлиненный додекаэдр и трапеции-ромбический додекаэдр вариации, наряду с ромбическими додекаэдрами, являются заполнение пространства. Есть множество другие додекаэдры.

В то время как правильный додекаэдр имеет много общих черт с другими Платоновыми телами, одно его уникальное свойство состоит в том, что можно начать с угла поверхности и провести бесконечное количество прямых линий через фигуру, которые возвращаются в исходную точку, не пересекаясь ни с одной другой. угол.^[1]

Правильные додекаэдры

Выпуклый правильный додекаэдр - один из пяти правильных Платоновы тела и может быть представлена ​​его Символ Шлефли {5, 3}.

В двойственный многогранник регулярный икосаэдр {3, 5} с пятью равносторонними треугольниками вокруг каждой вершины.

Четыре вида правильных додекаэдров

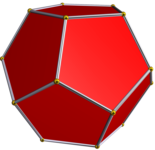Выпуклый правильный додекаэдр

Малый звездчатый додекаэдр

Большой додекаэдр

Большой звездчатый додекаэдр

Выпуклый правильный додекаэдр также имеет три звёздчатые, все из которых являются правильными звездчатыми додекаэдрами. Они составляют три из четырех Многогранники Кеплера – Пуансо. Они малый звездчатый додекаэдр {5/2, 5}, г. большой додекаэдр {5, 5/2}, а большой звездчатый додекаэдр {5/2, 3}. Малый звездчатый додекаэдр и большой додекаэдр двойственны друг другу; большой звездчатый додекаэдр двойственен большой икосаэдр {3, 5/2}. Все эти правильные звездные додекаэдры имеют правильную пятиугольную или пентаграмматический лица. Выпуклый правильный додекаэдр и большой звездчатый додекаэдр - разные реализации одного и того же абстрактный правильный многогранник; малый звездчатый додекаэдр и большой додекаэдр - разные реализации другого абстрактного правильного многогранника.

Другие пятиугольные додекаэдры

В кристаллография, два важных додекаэдра могут встречаться в виде кристаллов в некоторых классы симметрии из кубическая кристаллическая система которые топологически эквивалентны правильному додекаэдру, но менее симметричны: пиритоэдр с пиритоэдрическая симметрия, а тетартоид с тетраэдрическая симметрия:

Пиритоэдр

Пиритоэдр
(Видеть Вот для вращающейся модели.)
Многоугольник лица	неправильный пятиугольник
Диаграммы Кокстера
Лица	12
Края	30 (6 + 24)
Вершины	20 (8 + 12)
Группа симметрии	Тчас, [4,3+], (3 * 2), порядок 24
Группа вращения	Т, [3,3]+, (332), порядок 12
Двойной многогранник	Псевдоикосаэдр
Характеристики	лицо переходное
Сеть

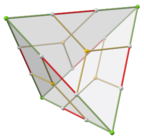
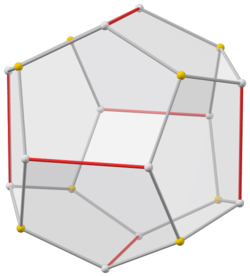
А пиритоэдр додекаэдр с пиритоэдрический (Т_час) симметрия. Словно правильный додекаэдр, в нем двенадцать одинаковых пятиугольник грани, по три пересечения в каждой из 20 вершин (см. рисунок).^[2] Однако пятиугольники не обязательно должны быть регулярными, и лежащее в основе атомное расположение не имеет истинной оси симметрии пятого порядка. Его 30 ребер разделены на два набора - по 24 и 6 ребер одинаковой длины. Единственные оси вращательная симметрия - три взаимно перпендикулярные оси второго порядка и четыре оси третьего порядка.

Хотя правильные додекаэдры не существуют в кристаллах, форма пиритоэдра встречается в кристаллах минерала. пирит, и это может быть вдохновением для открытия регулярных Платоново твердое тело форма. Настоящий правильный додекаэдр может иметь форму квазикристаллы (Такие как квазикристалл гольмия – магния – цинка ) с икосаэдрическая симметрия, который включает в себя истинные оси пятикратного вращения.

Кристаллический пирит

Пирит природный (с углами граней справа) Его название происходит от одного из двух распространенных кристальные привычки показано пирит (другой - куб ). В пиритоэдрическом пирите грани имеют Индекс Миллера из (210), что означает, что двугранный угол составляет 2 · arctan (2) ≈ 126,87 °, и каждая пятиугольная грань имеет один угол примерно 121,6 ° между двумя углами примерно 106,6 ° и двумя противоположными углами примерно 102,6 °. Следующие формулы показывают размеры грани идеального кристалла (который редко встречается в природе). ${displaystyle {ext {Height}} = {frac {sqrt {5}} {2}} cdot {ext {длинная сторона}}}$ ${displaystyle {ext {Width}} = {frac {4} {3}} cdot {ext {Long side}}}$ ${displaystyle {ext {Short side}} = {sqrt {frac {7} {12}}} cdot {ext {Long side}}}$

Декартовы координаты

Восемь вершин куба имеют координаты (± 1, ± 1, ± 1).

Те из 12 дополнительных вершин(0, ±(1 + час), ±(1 − час²)), (±(1 + час), ±(1 − час²), 0) и(±(1 − час²), 0, ±(1 + час)).

час это высота клин -образная «крыша» над гранями этого куба с длиной ребра 2.

Важный случай час = 1/2 (четверть длины ребра куба) для идеального природного пирита (также пиритоэдр в Структура Вира – Фелана ).

Еще один час = 1/φ = 0,618 ... для правильный додекаэдр. См. Раздел Геометрическая свобода для других случаев.

Два пиритоэдра с переставленными ненулевыми координатами находятся в двойных положениях друг относительно друга, как додекаэдры в соединение двух додекаэдров.

Ортографические проекции пиритоэдра с час = 1/2

Высота 1/2 и 1 /φ

Двойные позиции в пирите хрустальные модели

Анимации
Соты чередующихся выпуклых и вогнутых пиритоэдров высотой от ±1/φ	Высота от 0 (куб) и 1 (ромбический додекаэдр)

Геометрическая свобода

Пиритоэдр имеет геометрическую степень свободы с предельные случаи кубического выпуклый корпус на одном пределе коллинеарных ребер, а ромбический додекаэдр в качестве другого предела, когда 6 ребер вырождаются до нулевой длины. Правильный додекаэдр представляет собой специальный промежуточный случай, когда все ребра и углы равны.

Можно обойти эти предельные случаи, создав вогнутые или невыпуклые пиритоэдры. В эндододекаэдр вогнутая и равносторонняя; он может замощить пространство выпуклым правильным додекаэдром. Продолжая оттуда в том же направлении, мы переходим через вырожденный случай, когда двенадцать вершин совпадают в центре, и переходим к правильному большой звездчатый додекаэдр где все ребра и углы снова равны, а грани были искажены в правильные пентаграммы. С другой стороны, за ромбическим додекаэдром, мы получаем невыпуклый равносторонний додекаэдр с самопересекающимися равносторонними пятиугольными гранями в форме рыбы.

Частные случаи пиритоэдра
Версии с равными абсолютными значениями и противоположными знаками вместе образуют соты. (Сравнивать эта анимация.) Показано соотношение длин ребер, а именно длины ребер в наборе из 24 (соприкасающиеся вершины куба) к длинам в наборе из 6 (соответствующих граням куба).
Соотношение	1 : 1	0 : 1	1 : 1	2 : 1	1 : 1	0 : 1	1 : 1
час	−√5 + 1/2	−1	−√5 + 1/2	0	√5 − 1/2	1	√5 + 1/2
	−1,618...		−0,618...		0,618...		1,618...
Изображение	Обычная звезда, большой звездчатый додекаэдр, с регулярным пентаграмма лица	Вырождение, 12 вершин в центре	Вогнутый равносторонний додекаэдр, называемый эндододекаэдр.[требуется разъяснение ]	А куб можно разделить на пиритоэдр, разделив пополам все ребра и грани в чередующихся направлениях.	Правильный додекаэдр - это промежуточный случай с равными длинами ребер.	А ромбический додекаэдр является вырожденным случаем, когда 6 скрещенных точек уменьшены до нулевой длины.	Самопересекающийся равносторонний додекаэдр

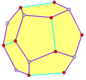
Тетартоид

Тетартоид Тетрагональный пятиугольный додекаэдр
(Видеть Вот для вращающейся модели.)
Многоугольник лица	неправильный пятиугольник
Обозначение Конвея	gT
Лица	12
Края	30 (6+12+12)
Вершины	20 (4+4+12)
Группа симметрии	Т, [3,3]+, (332), порядок 12
Характеристики	выпуклый, лицо переходное

А тетартоид (также тетрагональный пятиугольный додекаэдр, пятиугольник-тритетраэдр, и тетраэдр пятиугольник додекаэдр) - додекаэдр с киральным тетраэдрическая симметрия (Т). Словно правильный додекаэдр, в нем двенадцать одинаковых пятиугольник грани, по три встречи в каждой из 20 вершин. Однако пятиугольники не правильные, и фигура не имеет осей симметрии пятого порядка.

Хотя правильные додекаэдры не существуют в кристаллах, тетартоидная форма существует. Название тетартоид происходит от греческого корня, означающего одну четверть, потому что он имеет одну четверть полной октаэдрической симметрии и половину пиритоэдрической симметрии.^[3] Минерал кобальтит может иметь эту форму симметрии.^[4]

Абстракции, разделяющие твердое тело топология а симметрию можно создать из куба и тетраэдра. В кубе каждая грань разделена пополам наклонным краем. В тетраэдре каждое ребро делится на три части, и каждая из новых вершин соединяется с центром грани. (В Обозначения многогранника Конвея это гиротетраэдр.)

Ортографические проекции с 2-х и 3-х кратных осей

Кубическая и тетраэдрическая форма

Кобальтит

Связь с додекаэдром дьякис

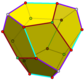
Тетартоид можно создать, увеличив 12 из 24 граней дякис додекаэдр. (Показанный здесь тетартоид основан на том, который сам создается путем увеличения 24 из 48 граней disdyakis додекаэдр.) Хиральный тетартоиды на основе додекаэдра dyakis в середине Хрустальная модель В модель кристалла справа показан тетартоид, образованный увеличением синих граней додекаэдрического ядра дьяки. Таким образом, края между синими гранями покрываются красными краями скелета.

Декартовы координаты

Следующие точки являются вершинами четырехугольника четырехугольника под тетраэдрическая симметрия:

(а, б, c); (−а, −б, c); (−п/d₁, −п/d₁, п/d₁); (−c, −а, б); (−п/d₂, п/d₂, п/d₂),

при следующих условиях:^[5]

0 ≤ а ≤ б ≤ c,

п = а²c − до н.э²,

d₁ = а² − ab + б² + ac − 2до н.э,

d₂ = а² + ab + б² − ac − 2до н.э,

nd₁d₂ ≠ 0.

Геометрическая свобода

В правильный додекаэдр тетартоид с более чем требуемой симметрией. В триакис тетраэдр - вырожденный случай с 12 ребрами нулевой длины. (С точки зрения использованных выше цветов это означает, что белые вершины и зеленые ребра поглощаются зелеными вершинами.)

Вариации тетартоида от правильный додекаэдр к триакис тетраэдр

Двойной треугольный гиробиантикупола

Форма более низкой симметрии правильного додекаэдра может быть построена как двойственная многограннику, построенному из двух треугольных антикупола связанная база-база, называемая треугольная гиробиантикупола. Имеет D_3D симметрия, порядок 12. Он имеет 2 набора по 3 одинаковых пятиугольника сверху и снизу, соединенных 6 пятиугольниками по бокам, которые чередуются вверх и вниз. Эта форма имеет шестиугольное поперечное сечение, и идентичные копии могут быть соединены как частичные шестиугольные соты, но все вершины не будут совпадать.

Ромбический додекаэдр

Ромбический додекаэдр

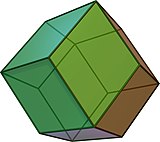
В ромбический додекаэдр это зоноэдр с двенадцатью ромбическими гранями и октаэдрической симметрией. Он двойственен квазирегулярный кубооктаэдр (ан Архимедово твердое тело ) и встречается в природе в виде кристалла. Ромбический додекаэдр собирается вместе, заполняя пространство.

В ромбический додекаэдр можно рассматривать как вырожденный пиритоэдр где 6 специальных ребер были уменьшены до нулевой длины, в результате чего пятиугольники превратились в ромбические грани.

Ромбический додекаэдр имеет несколько звездчатые, то первый из которых также параллелоэдрический заполнитель.

Другой важный ромбический додекаэдр - Додекаэдр Билинского, имеет двенадцать граней, совпадающих с лицами ромбический триаконтаэдр, т.е. диагонали находятся в соотношении Золотое сечение. Это также зоноэдр и был описан Билински в 1960 г.^[6] Эта цифра - еще один заполнитель пространства, и она также может встречаться в непериодических заполнение космоса наряду с ромбическим триаконтаэдром, ромбическим икосаэдром и ромбическими гексаэдрами.^[7]

Другие додекаэдры

Есть 6,384,634 топологически различных выпуклый додекаэдры, без зеркальных отображений - число вершин от 8 до 20.^[8] (Два многогранника являются «топологически разными», если они имеют внутренне различное расположение граней и вершин, так что невозможно преобразовать один в другой, просто изменяя длину ребер или углы между ребрами или гранями.)

Топологически различные додекаэдры (исключая пятиугольные и ромбические формы)

• Равномерные многогранники:
  • Десятиугольная призма - 10 квадратов, 2 декагона, D_10ч симметрия, порядок 40.
  • Пятиугольная антипризма - 10 равносторонних треугольников, 2 пятиугольника, D_5d симметрия, порядок 20
• Твердые тела Джонсона (обычное лицо):
  • Пятиугольный купол - 5 треугольников, 5 квадратов, 1 пятиугольник, 1 десятиугольник, C_5в симметрия, порядок 10
  • Курносый дисфеноид - 12 треугольников, D_2d, заказ 8
  • Удлиненная квадратная дипирамида - 8 треугольников и 4 квадрата, D_4ч симметрия, порядок 16
  • Метабидоуменьшенный икосаэдр - 10 треугольников и 2 пятиугольника, C_2v симметрия, порядок 4
• Конгруэнтное неправильное лицо: (лицо переходный )
  • Гексагональная бипирамида - 12 равнобедренных треугольники, двойной из шестиугольная призма, D_6ч симметрия, порядок 24
  • Шестиугольный трапецииэдр – 12 воздушные змеи, двойной из шестиугольная антипризма, D_6d симметрия, порядок 24
  • Тетраэдр Триаки - 12 равнобедренных треугольников, двойных из усеченный тетраэдр, Т_d симметрия, порядок 24
• Другое менее регулярное столкновение:
  • Хендекагональный пирамида - 11 равнобедренных треугольников и 1 правильный девичник, C_11в, заказ 11
  • Трапецо-ромбический додекаэдр - 6 ромбов, 6 трапеции - двойной треугольная ортобикупола, D_3ч симметрия, порядок 12
  • Ромбо-гексагональный додекаэдр или же удлиненный додекаэдр - 8 ромбов и 4 равносторонних шестиугольники, D_4ч симметрия, порядок 16
  • Усеченный пятиугольный трапецоэдр, D_5d, порядка 20, топологически эквивалентен правильному додекаэдру

Практическое использование

Арманд Шпиц использовал додекаэдр как "глобус" эквивалент его Проектор для планетария с цифровым куполом.^[9] на основе предложения от Альберт Эйнштейн.

Смотрите также

• 120 ячеек: а регулярный полихорон (4D многогранник), поверхность которого состоит из 120 додекаэдрических ячеек.
• Braarudosphaera bigelowii
• Додекаэдр пентакиса
• Римский додекаэдр
• Курносый додекаэдр
• Усеченный додекаэдр

Рекомендации

внешняя ссылка

• Вайсштейн, Эрик В. "Додекаэдр". MathWorld.
• Вайсштейн, Эрик В. «Удлиненный додекаэдр». MathWorld.
• Вайсштейн, Эрик В. «Пиритоэдр». MathWorld.
• Четвертое твердое тело Платона и "Пиритоэдр", Пол Стивенсон, 1993, The Mathematical Gazette, Vol. 77, № 479 (июл., 1993), стр. 220–226. [1]
• ГРЕЧЕСКИЕ ЭЛЕМЕНТЫ
• Звёздчатая форма пиритоэдра VRML-модели и анимации Пиритоэдра и его звёздчатые
• Клитцинг, Ричард. "3D выпуклые равномерные многогранники o3o5x - лань".
• Редактируемая печатная сетка додекаэдра с интерактивным трехмерным изображением
• Равномерные многогранники
• Оригами Многогранники - Модели из модульного оригами
• Додекаэдр - 3D-модель, которая работает в вашем браузере
• Многогранники виртуальной реальности Энциклопедия многогранников
  • Додекаэдры вариации
  • VRML модели
  1. Правильный додекаэдр обычный
  2. Ромбический додекаэдр квазирегулярный
  3. Десятиугольная призма вершинно-транзитивный
  4. Пятиугольная антипризма вершинно-транзитивный
  5. Гексагональная дипирамида лицо переходный
  6. Тетраэдр Триаки лицо переходный
  7. шестиугольный трапецииэдр лицо переходный
  8. Пятиугольный купол обычные лица
• K.J.M. Маклин, Геометрический анализ пяти платоновых тел и других полурегулярных многогранников
• Додекаэдр 3D визуализация
• Стелла: многогранник-навигатор: Программное обеспечение, использованное для создания некоторых изображений на этой странице.
• Как сделать додекаэдр из пенополистирольного куба
• Римские додекаэдры: загадочные объекты, обнаруженные на территории Римской империи.