Пятиугольный купол - Pentagonal cupola

Пятиугольный купол
Тип	Джонсон J4 - J5 - J6
Лица	5 треугольники 5 квадраты 1 пятиугольник 1 десятиугольник
Края	25
Вершины	15
Конфигурация вершины	10(3.4.10) 5(3.4.5.4)
Группа симметрии	C5в, [5], (*55)
Группа вращения	C5, [5]+, (55)
Двойной многогранник	-
Характеристики	выпуклый
Сеть

3D модель пятиугольного купола

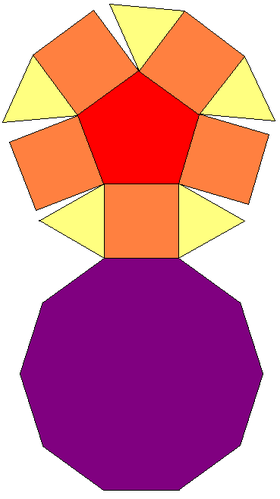В геометрия, то пятиугольник купол один из Твердые тела Джонсона (J₅). Его можно получить как кусочек ромбикосододекаэдр. Пятиугольный купол состоит из 5 равносторонние треугольники, 5 квадраты, 1 пятиугольник, и 1 десятиугольник.

А Джонсон солид один из 92 строго выпуклый многогранники который состоит из правильный многоугольник лица, но не униформа многогранники (т. е. не Платоновы тела, Архимедовы тела, призмы, или же антипризмы ). Их назвали Норман Джонсон, которые впервые перечислили эти многогранники в 1966 году.^[1]

Формулы

Следующее формулы за объем, площадь поверхности и по окружности можно использовать, если все лица находятся обычный, с длиной кромки а:^[2]

${ displaystyle V = left ({ frac {1} {6}} left (5 + 4 { sqrt {5}} right) right) a ^ {3} приблизительно 2.32405a ^ {3} ,}$

${ displaystyle A = left ({ frac {1} {4}} left (20 + 5 { sqrt {3}} + { sqrt {5 (145 + 62 { sqrt {5}})}) } right) right) a ^ {2} приблизительно 16.57975a ^ {2},}$

${ displaystyle R = left ({ frac {1} {2}} { sqrt {11 + 4 { sqrt {5}}}} right) a приблизительно 2.23295a.}$

В высота пятиугольного купола ^[3]

${ displaystyle h = { sqrt { frac {5 - { sqrt {5}}} {10}}} a приблизительно 0,52573a}$.

Связанные многогранники

Двойной многогранник

Двойник пятиугольного купола имеет 10 треугольных граней и 5 граней змея:

Двойной пятиугольный купол	Чистая двойная	3D модель

Другие выпуклые купола

Семейство выпуклых купола

[

• v
• т
• е

]

п	2	3	4	5	6
Имя	{2} || т {2}	{3} || т {3}	{4} || т {4}	{5} || т {5}	{6} || т {6}
Купол	Дигональный купол	Треугольный купол	Квадратный купол	Пятиугольный купол	Шестиугольный купол (Плоский)
Связанный униформа многогранники	Треугольная призма	Кубокта- эдр	Ромбовидный кубокта- эдр	Ромб- icosidodeca- эдр	Ромбовидный трехгексагональный черепица

Перекрещенный пентаграмматический купол

3D модель скрещенного пятиугольного купола

В геометрия, то скрещенный пентаграмматический купол один из невыпуклых Джонсон солид изоморфы, будучи топологически идентичными выпуклому пятиугольному куполу. Его можно получить как кусочек невыпуклый большой ромбоикосододекаэдр или квазиромбикосододекаэдр, аналогично тому, как пятиугольный купол может быть получен как срез ромбикосододекаэдра. Как и во всех куполах, основание многоугольник вдвое больше края и вершины как верхний; в этом случае базовый многоугольник декаграмма.

Его можно рассматривать как купол с ретроградным пентаграммическим основанием, так что квадраты и треугольники соединяются через основания в противоположном направлении от основания. пентаграмматический куплоид, следовательно, более глубоко пересекаются друг с другом.

Рекомендации

внешняя ссылка

• Эрик В. Вайсштейн, Пятиугольный купол (Джонсон солид ) в MathWorld.