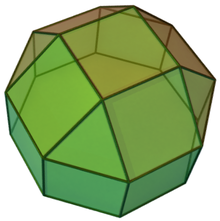
Вытянутый квадратный купол - Elongated square cupola

Вытянутый квадратный купол
Тип	Джонсон J18 - J19 - J20
Лица	4 треугольники 3x4 + 1 квадраты 1 восьмиугольник
Края	36
Вершины	20
Конфигурация вершины	8(42.8) 4+8(3.43)
Группа симметрии	C4в
Двойной многогранник	-
Характеристики	выпуклый
Сеть

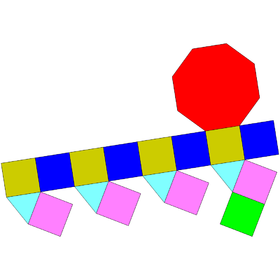В геометрия, то удлиненный квадратный купол один из Твердые тела Джонсона (J₁₉). Как следует из названия, его можно построить, удлинив квадратный купол (J₄), прикрепив восьмиугольная призма к его базе. Твердое тело можно рассматривать как ромбокубооктаэдр со своей «крышкой» (другой квадратный купол ) удаленный.

А Джонсон солид один из 92 строго выпуклый многогранники который состоит из правильный многоугольник лица, но не униформа многогранники (т. е. не Платоновы тела, Архимедовы тела, призмы, или же антипризмы ). Их назвали Норман Джонсон, которые впервые перечислили эти многогранники в 1966 году.^[1]

Формулы

Следующее формулы за объем, площадь поверхности и по окружности можно использовать, если все лица находятся обычный, с длиной кромки а:^[2]

${ displaystyle V = (3 + { frac {8 { sqrt {2}}} {3}}) a ^ {3} приблизительно 6,77124 ... a ^ {3}}$

${ displaystyle A = (15 + 2 { sqrt {2}} + { sqrt {3}}) a ^ {2} приблизительно 19,5605 ... a ^ {2}}$

${ displaystyle C = ({ frac {1} {2}} { sqrt {5 + 2 { sqrt {2}}}}) a приблизительно 1,39897 ... a}$

Двойной многогранник

Двойник вытянутого квадратного купола имеет 20 граней: 8 равнобедренных треугольников, 4 воздушных змея, 8 четырехугольников.

Двойной удлиненный квадратный купол	Чистая двойная

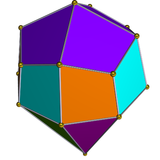Связанные многогранники и соты

Вытянутый квадратный купол заполняет пространство. соты с тетраэдры и кубики; с кубиками и кубооктаэдр; и с тетраэдрами, удлиненные квадратные пирамиды, и удлиненные квадратные бипирамиды. (Последние две единицы можно разложить на кубики и квадратные пирамиды.)^[3]

Рекомендации

внешняя ссылка

• Эрик В. Вайсштейн, Вытянутый квадратный купол (Джонсон солид ) в MathWorld.

Этот многогранник -связанная статья является заглушка. Вы можете помочь Википедии расширяя это.