Гиробикупола удлиненная квадратная - Elongated square gyrobicupola

Гиробикупола удлиненная квадратная
Удлиненный квадрат gyrobicupola.png
ТипДжонсон
J36 - J37 – J38
Лица8 треугольники
18 квадраты
Края48
Вершины24
Конфигурация вершины8+16(3.43)
Группа симметрииD4d
Двойной многогранникПсевдо-дельтовидный икоситетраэдр
Характеристикивыпуклый, единственное число вершина фигура
Сеть
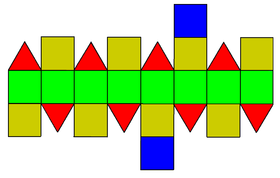Джонсон солид 37 net.png
3D модель вытянутой квадратной гиробикуполы

В геометрия, то удлиненная квадратная гиробикупола или же псевдоромбокубооктаэдр один из Твердые тела Джонсона (J37). Обычно это не считается Архимедово твердое тело, хотя его грани состоят из правильные многоугольники которые встречаются по одному и тому же шаблону в каждой из его вершин, потому что, в отличие от 13 архимедовых тел, в нем отсутствует набор глобальных симметрий, которые переводят каждую вершину в любую другую вершину (хотя Грюнбаум предложил добавить его в традиционный список архимедовых тел в качестве 14-го примера). Он сильно напоминает, но не должен быть принят за малый ромбокубооктаэдр, который является архимедово твердое тело. Это также канонический многогранник.

Эта форма могла быть обнаружена Иоганн Кеплер в его перечислении архимедовых тел, но его первое четкое появление в печати, по-видимому, принадлежит Дункан Соммервилл в 1905 г.[1] Он был независимо открыт заново Дж. С. П. Миллер к 1930 г. (по ошибке при попытке построить модель малый ромбокубооктаэдр[2]) и снова В. Г. Ашкинузе в 1957 г.[3]

А Джонсон солид один из 92 строго выпуклый многогранники который состоит из правильный многоугольник лица, но не униформа многогранники (т. е. не Платоновы тела, Архимедовы тела, призмы, или же антипризмы ). Их назвали Норман Джонсон, которые впервые перечислили эти многогранники в 1966 году.[4]

Построение и связь с ромбокубооктаэдром

Как следует из названия, его можно построить, удлинив квадратная гиробикупола (J29) и вставив восьмиугольный призма между двумя его половинами.

Маленький ромбокубооктаэдр.png
Ромбокубооктаэдр		Расчлененный ромбокубооктаэдр.png
Разорванные секции
ромбокубооктаэдр		Pseudorhombicuboctahedron.png
Псевдоромбокубооктаэдр

Твердое тело также можно увидеть в результате скручивания одного из квадратные купола (J4) на ромбокубооктаэдр (один из Архимедовы тела; он же удлиненный квадратный ортобикупола) на 45 градусов. Следовательно, это круговой ромбокубооктаэдр. Его сходство с ромбокубооктаэдром дает ему альтернативное название псевдоромбокубооктаэдр. Иногда его называют «четырнадцатым архимедовым телом».

Это свойство не распространяется на его пятиугольный аналог, спиральный ромбикосододекаэдр.

Симметрия и классификация

3D модель псевдодельтоидального икоситетраэдра

Псевдоромбокубооктаэдр обладает D4d симметрия. Он локально вершинно-регулярный - расположение четырех граней, инцидентных каждой вершине, одинаково для всех вершин; это уникальное явление среди твердых тел Джонсона. Однако способ, которым он «скручен», дает ему отчетливый «экватор» и два различных «полюса», которые, в свою очередь, делят его вершины на 8 «полярных» вершин (по 4 на полюс) и 16 «экваториальных» вершин. Следовательно, это не вершинно-транзитивный, и, следовательно, обычно не считается одним из Архимедовы тела.

С лицами, окрашенными его D4d симметрия, это может выглядеть так:

В псевдо-дельтовидный икоситетраэдр (справа) это двойственный многогранник.
Джонсон солид 37.pngДжонсон солид 37 net.pngПсевдостромбический icositetrahedron.pngПсевдостромбический икозитетраэдр flat.png

Вокруг него 8 (зеленых) квадратов. экватор, 4 (красных) треугольника и 4 (желтых) квадрата сверху и снизу и по одному (синему) квадрату на каждом полюсе.

Связанные многогранники и соты

Вытянутая квадратная гиробикупола может образовывать заполнитель пространства. соты с регулярным тетраэдр, куб и кубооктаэдр. Он также может образовывать еще одну соту с тетраэдром, квадратная пирамида и различные комбинации кубиков, удлиненные квадратные пирамиды, и удлиненные квадратные бипирамиды.[5]

В псевдо большой ромбокубооктаэдр

В псевдо большой ромбокубооктаэдр - невыпуклый аналог псевдоромбокубооктаэдра, построенный аналогичным образом из невыпуклый большой ромбокубооктаэдр.

В химии

Поливанадат-ион [V18О42]12− имеет псевдоромбокубооктаэдрическую структуру, где каждая квадратная грань выступает в качестве основания ВО.5 пирамида.[6]

Рекомендации

  1. ^ Соммервилл, Д. М. Я. (1905), «Полурегулярные сети плоскости в абсолютной геометрии», Сделки Королевского общества Эдинбурга, 41: 725–747, Дои:10,1017 / с0080456800035560. Как цитирует Грюнбаум (2009).
  2. ^ Роуз Болл (1939), Кокстер, Х. С. М. (ред.), Математические развлечения и эссе (11-е изд.), С. 137
  3. ^ Грюнбаум, Бранко (2009), «Постоянная ошибка» (PDF), Elemente der Mathematik, 64 (3): 89–101, Дои:10.4171 / EM / 120, МИСТЕР  2520469 Перепечатано в Pitici, Mircea, ed. (2011). Лучшая работа по математике 2010 г.. Издательство Принстонского университета. С. 18–31..
  4. ^ Джонсон, Норман В. (1966), «Выпуклые многогранники с правильными гранями», Канадский математический журнал, 18: 169–200, Дои:10.4153 / cjm-1966-021-8, МИСТЕР  0185507, Zbl  0132.14603.
  5. ^ «Соты J37», Галерея деревянных многогранников, получено 2016-03-21
  6. ^ Гринвуд, Норман Н.; Эрншоу, Алан (1997). Химия элементов (2-е изд.). Баттерворт-Хайнеманн. п. 986. ISBN  978-0-08-037941-8.

дальнейшее чтение

  • Энтони Пью (1976), Многогранники: визуальный подход, Калифорния: Калифорнийский университет Press в Беркли, ISBN  0-520-03056-7 Глава 2: Архимедовы многогранники, призмы и антипризмы, с. 25 Псевдо-ромбокубооктаэдр

внешняя ссылка