Пентагон - Википедия - Pentagon

Пентагон
Равносторонний пятиугольник, то есть пятиугольник, все пять сторон которого имеют одинаковую длину.
Края и вершины	5
Внутренний угол (градусы )	108 ° (при равноугловом, включая обычный)

В геометрия, а пятиугольник (от Греческий πέντε пенте и γωνία гония, смысл пять и угол^[1]) любое пятистороннее многоугольник или 5-угольник. Сумма внутренние углы в просто пятиугольник равен 540 °.

Пентагон может быть простым или самопересекающийся. Самопересекающийся правильный пятиугольник (или же звезда пятиугольник) называется пентаграмма.

Правильные пятиугольники

Правильный пятиугольник
Правильный пятиугольник
Тип	Правильный многоугольник
Края и вершины	5
Символ Шлефли	{5}
Диаграмма Кокстера
Группа симметрии	Двугранный (D5), порядок 2 × 5
Внутренний угол (градусы )	108°
Двойной многоугольник	Себя
Характеристики	Выпуклый, циклический, равносторонний, изогональный, изотоксальный

Сторона (${ displaystyle t}$), радиус описанной окружности (${ displaystyle R}$), радиус вписанной окружности (${ displaystyle r}$), высота (${ displaystyle R + r}$), ширина / диагональ (${ displaystyle varphi t}$)

А обычный пятиугольник имеет Символ Шлефли {5} и внутренние углы равны 108 °.

А обычный пятиугольник имеет пять строк отражательная симметрия, и вращательная симметрия порядка 5 (через 72 °, 144 °, 216 ° и 288 °). В диагонали из выпуклый правильный пятиугольник в Золотое сечение по бокам. Его высота (расстояние от одной стороны до противоположной вершины) и ширина (расстояние между двумя наиболее удаленными друг от друга точками, равное длине диагонали) задаются выражением

${ displaystyle { text {Height}} = { frac { sqrt {5 + 2 { sqrt {5}}}} {2}} cdot { text {Side}} примерно 1,539 cdot { текст {Side}},}$

${ displaystyle { text {Width}} = { text {Diagonal}} = { frac {1 + { sqrt {5}}} {2}} cdot { text {Side}} приблизительно 1,618 cdot { text {Side}},}$

${ displaystyle { text {Width}} = { sqrt {2 - { frac {2} { sqrt {5}}}}} cdot { text {Height}} приблизительно 1.051 cdot { text {Высота}},}$

${ displaystyle { text {Diagonal}} = R { sqrt { frac {5 + { sqrt {5}}} {2}}} = 2R cos 18 ^ { circ} = 2R cos { frac { pi} {10}} приблизительно 1,902R,}$

куда р это радиус описанный круг.

Площадь правильного выпуклого пятиугольника с длиной стороны т дан кем-то

${ displaystyle A = { frac {t ^ {2} { sqrt {25 + 10 { sqrt {5}}}}} {4}} = { frac {5t ^ {2} tan (54 ^ { circ})} {4}} = { frac {{ sqrt {5 (5 + 2 { sqrt {5}})}} t ^ {2}} {4}} приблизительно 1,720t ^ { 2}.}$

А пентаграмма или пятиугольник - это обычный звезда пятиугольник. Его Символ Шлефли составляет {5/2}. Его стороны образуют диагонали правильного выпуклого пятиугольника - в таком расположении стороны двух пятиугольников находятся в Золотое сечение.

Когда правильный пятиугольник ограниченный по кругу с радиусом р, длина его края т дается выражением

${ displaystyle t = R { sqrt { frac {5 - { sqrt {5}}} {2}}} = 2R sin 36 ^ { circ} = 2R sin { frac { pi} {5}} около 1,176Р,}$

и его площадь

${ displaystyle A = { frac {5R ^ {2}} {4}} { sqrt { frac {5 + { sqrt {5}}} {2}}};}$

так как площадь описанной окружности равна ${ displaystyle pi R ^ {2},}$ правильный пятиугольник заполняет приблизительно 0,7568 описанной окружности.

Вывод формулы площади

Площадь любого правильного многоугольника равна:

${ displaystyle A = { frac {1} {2}} Pr}$

куда п периметр многоугольника, а р это inradius (эквивалентно апофема ). Подставляя значения регулярного пятиугольника на п и р дает формулу

${ displaystyle A = { frac {1} {2}} cdot 5t cdot { frac {t tan (54 ^ { circ})} {2}} = { frac {5t ^ {2} tan (54 ^ { circ})} {4}}}$

с длиной стороны т.

Inradius

Как и любой правильный выпуклый многоугольник, правильный выпуклый пятиугольник имеет вписанный круг. В апофема, который является радиусом р вписанной окружности, правильного пятиугольника связана с длиной стороны т к

${ displaystyle r = { frac {t} {2 tan ( pi / 5)}} = { frac {t} {2 { sqrt {5 - { sqrt {20}}}}}} примерно 0,6882 cdot т.}$

Хорды ​​от описанной окружности к вершинам

Как и любой правильный выпуклый многоугольник, правильный выпуклый пятиугольник имеет описанный круг. Для правильного пятиугольника с последовательными вершинами A, B, C, D, E, если P - любая точка на описанной окружности между точками B и C, то PA + PD = PB + PC + PE.

Точка в плоскости

Для произвольной точки на плоскости правильного пятиугольника с описанным радиусом ${ displaystyle R}$, расстояние до центра тяжести правильного пятиугольника и его пяти вершин равно ${ displaystyle L}$ и ${ displaystyle d_ {i}}$ соответственно имеем ^[2]

${ displaystyle textstyle sum _ {i = 1} ^ {5} d_ {i} ^ {2} = 5 (R ^ {2} + L ^ {2}),}$

${ displaystyle textstyle sum _ {i = 1} ^ {5} d_ {i} ^ {4} = 5 ((R ^ {2} + L ^ {2}) ^ {2} + 2R ^ {2 } L ^ {2}),}$

${ displaystyle textstyle sum _ {i = 1} ^ {5} d_ {i} ^ {6} = 5 ((R ^ {2} + L ^ {2}) ^ {3} + 6R ^ {2 } L ^ {2} (R ^ {2} + L ^ {2})),}$

${ displaystyle textstyle sum _ {i = 1} ^ {5} d_ {i} ^ {8} = 5 ((R ^ {2} + L ^ {2}) ^ {4} + 12R ^ {2 } L ^ {2} (R ^ {2} + L ^ {2}) ^ {2} + 6R ^ {4} L ^ {4}).}$

Если ${ displaystyle d_ {i}}$ - расстояния от вершин правильного пятиугольника до любой точки его описанной окружности, то ^[2]

${ displaystyle 3 ( textstyle sum _ {i = 1} ^ {5} d_ {i} ^ {2}) ^ {2} = 10 textstyle sum _ {i = 1} ^ {5} d_ { i} ^ {4}.}$

Построение правильного пятиугольника

Правильный пятиугольник можно построить с компас и линейка, поскольку 5 - это Ферма Прайм. Известно множество методов построения правильного пятиугольника. Некоторые обсуждаются ниже.

Метод Ричмонда

Один из способов построения правильного пятиугольника в данном круге описан Ричмондом.^[3] и далее обсуждается в работе Кромвеля. Многогранники.^[4]

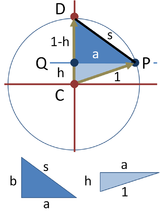
На верхней панели показана конструкция, использованная в методе Ричмонда для создания стороны вписанного пятиугольника. Окружность, определяющая пятиугольник, имеет единичный радиус. Его центр расположен в точке C и середина M отмечен на полпути по радиусу. Эта точка присоединяется к периферии вертикально над центром в точке D. Угол CMD делится пополам, а биссектриса пересекает вертикальную ось в точке Q. Горизонтальная линия через Q пересекает круг в точке п, и аккорд PD - искомая сторона вписанного пятиугольника.

Чтобы определить длину этой стороны, два прямоугольных треугольника DCM и QCM изображены под кружком. С помощью Теорема Пифагора и двух сторон, гипотенуза большего треугольника находится как ${ displaystyle scriptstyle { sqrt {5}} / 2}$. Сторона час меньшего треугольника находится с помощью формула полуугла:

${ Displaystyle загар ( фи / 2) = { гидроразрыва {1- соз ( фи)} { грех ( фи)}} ,}$

где косинус и синус ϕ известны из большего треугольника. Результат:

${ displaystyle h = { frac {{ sqrt {5}} - 1} {4}} .}$

Когда эта сторона известна, внимание обращается на нижнюю диаграмму, чтобы найти сторону s правильного пятиугольника. Во-первых, сторона а правого треугольника находится снова с помощью теоремы Пифагора:

${ displaystyle a ^ {2} = 1-h ^ {2} ; a = { frac {1} {2}} { sqrt { frac {5 + { sqrt {5}}} {2 }}} .}$

потом s находится с помощью теоремы Пифагора и левого треугольника как:

${ displaystyle s ^ {2} = (1-h) ^ {2} + a ^ {2} = (1-h) ^ {2} + 1-h ^ {2} = 1-2h + h ^ { 2} + 1-h ^ {2} = 2-2h = 2-2 left ({ frac {{ sqrt {5}} - 1} {4}} right) }$

${ displaystyle = { frac {5 - { sqrt {5}}} {2}} .}$

Сторона s следовательно является:

${ displaystyle s = { sqrt { frac {5 - { sqrt {5}}} {2}}} ,}$

хорошо зарекомендовавший себя результат.^[5] Следовательно, такая конструкция пятиугольника верна.

Карлайл круги

Метод с использованием кругов Карлайла

Круг Карлайла был изобретен как геометрический метод для поиска корней квадратное уровненеие.^[6] Эта методика приводит к процедуре построения правильного пятиугольника. Шаги следующие:^[7]

1. Нарисовать круг в который вписать пятиугольник и отметить центральную точку О.
2. Проведите горизонтальную линию через центр круга. Отметьте левое пересечение с кругом точкой B.
3. Проведите вертикальную линию через центр. Отметьте одно пересечение с кругом как точку А.
4. Постройте точку M как середина О и B.
5. Нарисуйте круг с центром в M через точку А. Отметьте его пересечение с горизонтальной линией (внутри исходного круга) как точку W и его пересечение вне круга как точка V.
6. Нарисуйте круг радиуса OA и центр W. Он пересекает исходный круг в двух вершинах пятиугольника.
7. Нарисуйте круг радиуса OA и центр V. Он пересекает исходный круг в двух вершинах пятиугольника.
8. Пятая вершина - это крайнее правое пересечение горизонтальной линии с исходной окружностью.

Шаги 6–8 эквивалентны следующей версии, показанной на анимации:

6а. Постройте точку F как середину точек O и W.

7а. Постройте вертикальную линию через F. Она пересекает исходную окружность в двух вершинах пятиугольника. Третья вершина - это крайнее правое пересечение горизонтальной линии с исходной окружностью.

8а. Постройте две другие вершины, используя циркуль и длину вершины, найденную на шаге 7a.

Использование тригонометрии и теоремы Пифагора

Использование тригонометрии и теоремы Пифагора для построения правильного пятиугольника.

Конструкция

1. Прежде всего отметим, что правильный пятиугольник можно разделить на 10 равных треугольников, как показано на рисунке. Наблюдение. Кроме того, cos 36 ° = ${ displaystyle { tfrac {1 + { sqrt {5}}} {4}}}$.†
2. В Шаг 1, мы используем четыре единицы (показаны синим) и прямой угол, чтобы построить отрезок длиной 1+√5, в частности, путем создания 1-2-√5 прямоугольный треугольник, а затем продолжая гипотенузу √5 на длину 1. Затем мы делим этот сегмент пополам, а затем снова делим пополам, чтобы получить отрезок длины ${ displaystyle { tfrac {1 + { sqrt {5}}} {4}}}$ (показан красным.)
3. В Шаг 2, построим две концентрические окружности с центром в О с радиусами 1 и длиной ${ displaystyle { tfrac {1 + { sqrt {5}}} {4}}}$. Затем мы помещаем п произвольно на меньшем круге, как показано. Построение линии перпендикулярно OP проходя через п, мы строим первую сторону пятиугольника, используя точки, созданные на пересечении касательной и единичной окружности. Копирование этой длины четыре раза по внешнему краю единичных кругов дает нам правильный пятиугольник.

† Доказательство того, что cos 36 ° = ${ displaystyle { tfrac {1 + { sqrt {5}}} {4}}}$

${ displaystyle 0 = cos 90 ^ { circ}}$

${ displaystyle = cos (72 ^ { circ} +18 ^ { circ})}$

${ displaystyle = cos 72 ^ { circ} cos 18 ^ { circ} - sin 72 ^ { circ} sin 18 ^ { circ}}$ (с использованием формула сложения углов для косинуса )

${ displaystyle = (2 cos ^ {2} 36 ^ { circ} -1) { sqrt { tfrac {1+ cos 36 ^ { circ}} {2}}} - 2 sin 36 ^ { circ} cos 36 ^ { circ} { sqrt { tfrac {1- cos 36 ^ { circ}} {2}}}}$ (с помощью формулы двойного и половинного угла )

Позволять ты = cos 36 °. Прежде всего отметим, что 0 < ты <1 (что поможет нам упростить работу). Сейчас же,

${ displaystyle { begin {align} 0 & {} = (2u ^ {2} -1) { sqrt { tfrac {1 + u} {2}}} - 2 { sqrt {1-u ^ {2 }}} cdot u { sqrt { tfrac {1-u} {2}}} 2 { sqrt {1-u ^ {2}}} cdot u { sqrt { tfrac {1- u} {2}}} & {} = (2u ^ {2} -1) { sqrt { tfrac {1 + u} {2}}} 2 { sqrt {1 + u}} { sqrt {1-u}} cdot u { sqrt {1-u}} & {} = (2u ^ {2} -1) { sqrt {1 + u}} 2u (1-u) & {} = 2u ^ {2} -1 2u-2u ^ {2} & {} = 2u ^ {2} -1 0 & {} = 4u ^ {2} -2u-1 u & {} = { frac {2 + { sqrt {(-2) ^ {2} -4 (4) (- 1)}}} {2 (4)}} u & {} = { frac {1+ { sqrt {5}}} {4}} end {align}}}$

Это быстро следует из знания, что удвоение синуса 18 градусов является обратным золотым сечением, которое мы знаем геометрически из треугольника с углами 72,72,36 градусов. Из тригонометрии мы знаем, что косинус дважды 18 градусов равен 1 минус два квадрата синуса 18 градусов, и это сводится к желаемому результату с помощью простой квадратичной арифметики.

Длина стороны указана

Правильный пятиугольник по Золотое сечение, разделение отрезка на внешнее деление

Пентагон при заданной длине стороны

1. Нарисуйте сегмент AB длина которого равна заданной стороне пятиугольника.
2. Расширить сегмент BA с точки А около трех четвертей сегмента BA.
3. Нарисуйте дугу круга, центральную точку B, с радиусом AB.
4. Нарисуйте дугу круга, центральную точку А, с радиусом AB; возникает перекресток F.
5. Постройте перпендикуляр к отрезку AB через точку F; возникает перекресток грамм.
6. Проведите линию, параллельную отрезку FG с точки А к дуге окружности вокруг точки А; возникает перекресток ЧАС.
7. Нарисуйте дугу круга, центральную точку грамм с радиусом GH к продолжению сегмента AB; возникает перекресток J.
8. Нарисуйте дугу круга, центральную точку B с радиусом Минет к перпендикуляру в точке грамм; возникает перекресток D на перпендикуляре, а пересечение E с дугой окружности, созданной вокруг точки А.
9. Нарисуйте дугу круга, центральную точку D, с радиусом BA пока эта дуга окружности не пересечет другую дугу окружности вокруг точки B; возникает перекресток C.
10. Соедините точки BCDEA. Получается пятиугольник.

Золотое сечение

${ displaystyle { frac { overline {BJ}} { overline {AB}}} = { frac { overline {AB}} { overline {AJ}}} = { frac {1 + { sqrt {5}}} {2}} = varphi приблизительно 1,618}$

Метод Евклида

Метод Евклида для пятиугольника в заданной окружности с использованием золотой треугольник, анимация 1 мин 39 с

Правильный пятиугольник - это конструктивный используя компас и линейка, либо вписав один в заданный круг, либо построив его на заданном крае. Этот процесс описал Евклид в его Элементы около 300 г. до н. э.^[8][9]

Просто с помощью транспортира (не классическая конструкция)

Ниже приводится прямой метод с использованием степеней:

1. Нарисуйте круг и выберите точку пятиугольника (например, верхний центр)
2. Выберите точку А на круге, который будет одной вершиной пятиугольника. Проведите линию через О и А.
3. Проведите через него направляющую линию и центр круга.
4. Нарисуйте линии под углом 54 ° (от направляющей), пересекающие точку пятиугольника.
5. Там, где они пересекают круг, нарисуйте линии под углом 18 ° (от параллели к направляющей).
6. Присоединяйтесь к тому месту, где они пересекают круг

После образования правильного выпуклого пятиугольника, если соединить несмежные углы (нарисовать диагонали пятиугольника), то получится пентаграмма, с меньшим правильным пятиугольником в центре. Или, если расширить стороны, пока не встретятся несмежные стороны, получится пентаграмма большего размера. Точность этого метода зависит от точности транспортира, используемого для измерения углов.

Физические методы

Узел сверху бумажной полосы

• Правильный пятиугольник можно создать из полоски бумаги, связав узел сверху в полоску и аккуратно расправив узел, потянув за концы полоски бумаги. Загибая один из концов над пятиугольником, можно увидеть пентаграмма при подсветке.
• Постройте регулярный шестиугольник на плотной бумаге или картоне. Сделайте складку по трем диаметрам между противоположными вершинами. Вырежьте от одной вершины к центру, чтобы получился равносторонний треугольный лоскут. Закрепите эту заслонку под своим соседом, чтобы пятиугольная пирамида. Основание пирамиды - правильный пятиугольник.

Симметрия

Симметрии правильного пятиугольника. Вершины окрашены в соответствии с их положением симметрии. Синие зеркальные линии проводятся через вершины и ребра. В центре даны приказы гирации.

В правильный пятиугольник имеет Dih₅ симметрия, порядок 10. Поскольку 5 - простое число есть одна подгруппа с диэдральной симметрией: Dih₁, и 2 циклическая группа симметрии: Z₅, а Z₁.

Эти 4 симметрии можно увидеть в 4 различных симметриях на пятиугольнике. Джон Конвей маркирует их буквой и групповым порядком.^[10] Полная симметрия правильной формы r10 и симметрия не помечена а1. Диэдральные симметрии разделяются в зависимости от того, проходят ли они через вершины (d для диагонали) или краев (п для перпендикуляров), и я когда линии отражения проходят через ребра и вершины. Циклические симметрии в среднем столбце помечены как грамм для их приказов центрального вращения.

Симметрия каждой подгруппы допускает одну или несколько степеней свободы для неправильных форм. Только g5 подгруппа не имеет степеней свободы, но может рассматриваться как направленные края.

Равносторонние пятиугольники

Равносторонний пятиугольник, состоящий из четырех равных кругов, расположенных в виде цепочки.

Равносторонний пятиугольник - это многоугольник с пятью сторонами равной длины. Однако его пять внутренних углов могут принимать ряд наборов значений, что позволяет ему образовывать семейство пятиугольников. Напротив, правильный пятиугольник уникален. вплоть до подобие, потому что оно равностороннее и равноугольное (его пять углов равны).

Циклические пятиугольники

А циклический пятиугольник - это тот, у которого окружность, называемая описанной окружностью, проходит через все пять вершин. Правильный пятиугольник - это пример циклического пятиугольника. Площадь циклического пятиугольника, правильного или неправильного, может быть выражена как одна четвертая квадратного корня одного из корней септическое уравнение коэффициенты которого являются функциями сторон пятиугольника.^[11][12][13]

Существуют циклические пятиугольники с рациональными сторонами и рациональной площадью; они называются Пентагоны Роббинса. В пятиугольнике Роббинса либо все диагонали рациональны, либо все иррациональны, и предполагается, что все диагонали должны быть рациональными.^[14]

Общие выпуклые пятиугольники

Для всех выпуклых пятиугольников сумма квадратов диагоналей меньше, чем в 3 раза больше суммы квадратов сторон.^{[15]:стр.75, № 1854}

Графики

K₅ полный график часто рисуется как правильный пятиугольник со всеми 10 соединенными ребрами. Этот график также представляет собой орфографическая проекция 5 вершин и 10 ребер 5-элементный. В выпрямленный 5-элементный, с вершинами на серединах краев 5-ячейки проецируется внутрь пятиугольника.

5-элементный (4D)

Выпрямленный 5-элементный (4D)

Примеры пятиугольников

Растения

• 

  Пятиугольное сечение окра.

• 

  Утренняя слава, как и многие другие цветы, имеют пятиугольную форму.

• 

  В гинецей из яблоко содержит пять плодолистиков, расположенных в пятиконечная звезда

• 

  Старфрут - еще один фрукт с пятикратной симметрией.

Животные

• 

  А морская звезда. Много иглокожие имеют пятикратную радиальную симметрию.

• 

  Другой пример иглокожих, a морской еж эндоскелет.

• 

  Иллюстрация хрупкие звезды, также иглокожие пятиугольной формы.

Минералы

• 

  Икосаэдр Ho-Mg-Zn квазикристалл в форме пятиугольника додекаэдр. Лица - правильные правильные пятиугольники.

• 

  А пиритоэдрический кристалл пирит. Пиритоэдр имеет 12 одинаковых пятиугольных граней, которые не обязательно должны быть правильными.

Искусственный

• 

  Пентагон, штаб-квартира Министерство обороны США.

• 

  Главная пластина из бейсбольное поле

Пентагоны в плитке

В самая известная упаковка правильных пятиугольников одинакового размера на плоскости есть двойная решетка структура, которая покрывает 92,131% плоскости.

Правильный пятиугольник не может появляться ни в одной мозаике из правильных многоугольников. Во-первых, доказать, что пятиугольник не может образовывать обычная черепица (тот, в котором все грани совпадают, что требует, чтобы все многоугольники были пятиугольниками), обратите внимание, что 360° / 108° = 3​¹⁄₃ (где 108 ° - внутренний угол), который не является целым числом; следовательно, не существует целого числа пятиугольников, разделяющих одну вершину и не оставляющих промежутков между ними. Сложнее доказать, что пятиугольник не может входить в состав любой мозаики от края до края, образованной правильными многоугольниками:

Максимально известный плотность упаковки правильного пятиугольника составляет примерно 0,921, что достигается двойная решетка Показанная упаковка. В препринте, выпущенном в 2016 году, Томас Хейлз и Wöden Kusner объявили доказательство того, что двойная решетчатая упаковка правильного пятиугольника (которую они называют упаковкой «пятиугольного ледяного луча» и которую они прослеживают до работы китайских ремесленников в 1900 году) имеет оптимальную плотность среди всех упаковок обычного пятиугольника. пятиугольники в плоскости.^[16] По состоянию на 2020 год^{[Обновить]}, их доказательства еще не реферированы и не опубликованы.

Не существует комбинаций правильных многоугольников с 4 или более, пересекающимися в вершине, содержащими пятиугольник. Для комбинаций с 3, если 3 многоугольника пересекаются в вершине и один имеет нечетное число сторон, другие 2 должны быть конгруэнтными. Причина этого в том, что многоугольники, соприкасающиеся с краями пятиугольника, должны чередоваться вокруг пятиугольника, что невозможно из-за нечетного количества сторон пятиугольника. Для пятиугольника получается многоугольник, все углы которого равны (360 − 108) / 2 = 126°. Чтобы найти количество сторон у этого многоугольника, результат: 360 / (180 − 126) = 6​²⁄₃, что не является целым числом. Следовательно, пятиугольник не может появиться ни в одной мозаике из правильных многоугольников.

Есть 15 классов пятиугольников, которые могут моноэдрально выложить плоскость. Ни один из пятиугольников не обладает какой-либо симметрией в целом, хотя у некоторых есть особые случаи с зеркальной симметрией.

15 одноугольных пятиугольных плиток

1	2	3	4	5
6	7	8	9	10
11	12	13	14	15

Пентагоны в многогранниках

ячас	Тчас	Тd	О	я	D5d
Додекаэдр	Пиритоэдр	Тетартоид	Пятиугольный икоситетраэдр	Пятиугольный шестиугольник	Усеченный трапецоэдр

Смотрите также

• Ассоциэдр; Пентагон - это ассоциаэдр четвертого порядка.
• Додекаэдр, многогранник правильной формы состоит из 12 пятиугольных граней
• Золотое сечение
• Список геометрических фигур
• Пятиугольные числа
• Пентаграмма
• Карта пентаграммы
• Pentastar, логотип Chrysler
• Теорема Пифагора # Подобные фигуры с трех сторон
• Тригонометрические константы пятиугольника

Встроенные заметки и ссылки

внешняя ссылка

• Вайсштейн, Эрик В. «Пентагон». MathWorld.
• Анимированная демонстрация построение вписанного пятиугольника с помощью циркуля и линейки.
• Как построить правильный пятиугольник только с компасом и линейкой.
• Как сложить правильный пятиугольник используя только полоску бумаги
• Определение и свойства пятиугольника, с интерактивной анимацией
• Примерные построения правильных пятиугольников художниками эпохи Возрождения
• Пентагон. Как рассчитать различные размеры правильных пятиугольников.