Семиугольник - Heptagon
| Обычный семиугольник | |
|---|---|
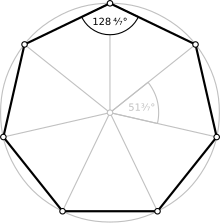 Обычный семиугольник | |
| Тип | Правильный многоугольник |
| Края и вершины | 7 |
| Символ Шлефли | {7} |
| Диаграмма Кокстера | |
| Группа симметрии | Двугранный (D7), порядок 2 × 7 |
| Внутренний угол (градусы ) | ≈128.571° |
| Двойной многоугольник | Себя |
| Характеристики | Выпуклый, циклический, равносторонний, изогональный, изотоксальный |
В геометрия, а семиугольник семигранный многоугольник или 7-угольник.
Гептагон иногда называют септагон, используя "септ-" ( элизия из септуа, а латинский -полученный числовой префикс, скорее, чем гепта-, а Греческий -производный числовой префикс; оба являются родственными) вместе с греческим суффиксом «-agon», означающим угол.
Обычный семиугольник
А обычный семиугольник, в котором все стороны и все углы равны, имеет внутренние углы из 5π / 7 радианы (1284⁄7 градусы ). Его Символ Шлефли равно {7}.
Площадь
Площадь (А) правильного семиугольника длины стороны а дан кем-то:
Это можно увидеть, разделив семиугольник с единичной стороной на семь треугольных «кусочков пирога» с вершинами в центре и в вершинах семиугольника, а затем разделив каждый треугольник пополам с помощью апофема как общая сторона. Апофема равна половине котангенса а площадь каждого из 14 маленьких треугольников составляет одну четвертую апофемы.
Точный алгебраическое выражение, начиная с кубический многочлен 8Икс3 + 4Икс2 − 4Икс − 1 (один из которых корни является )[1] дается в сложные числа к:
в котором мнимые части компенсируют друг друга, оставляя выражение с действительным знаком. Это выражение нельзя алгебраически переписать без сложных компонентов, так как указанное кубическая функция является казус несокрушимый.
Площадь правильного семиугольника вписанный в кругу радиус р является в то время как площадь самого круга таким образом, правильный семиугольник заполняет примерно 0,8710 своей площади. описанный круг.
Строительство
Поскольку 7 - это Pierpont Prime но не Ферма Прайм, правильный семиугольник не конструктивный с компас и линейка но строится с пометкой линейка и компас. Это самый маленький правильный многоугольник с этим свойством. Такой тип конструкции называется конструкция Neusis. Его также можно построить с помощью циркуля, линейки и трисектора угла. Невозможность построения линейки и циркуля следует из наблюдения, что является нулем несводимый кубический Икс3 + Икс2 − 2Икс − 1. Следовательно, этот многочлен является минимальный многочлен из 2cos (2π⁄7), тогда как степень минимального многочлена для конструктивное число должно быть степенью 2.
 А конструкция Neusis внутреннего угла в правильный семиугольник. | 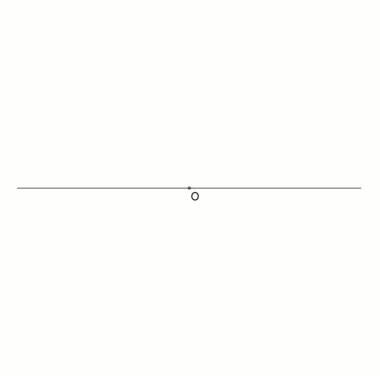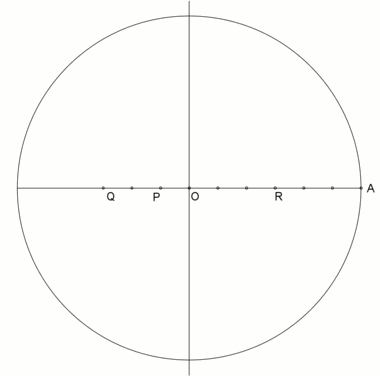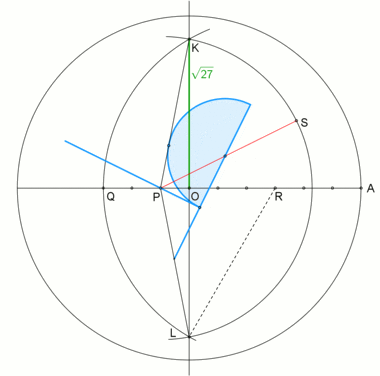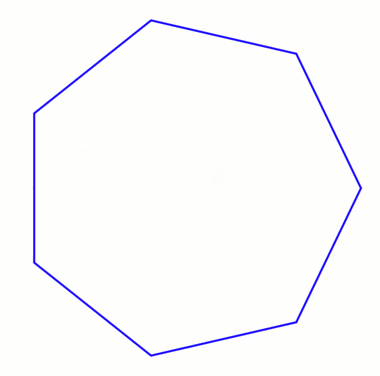 Анимация из конструкции neusis с радиусом описанной окружности , в соответствии с Эндрю М. Глисон[1] на основе трисекция угла с помощью Томагавк. Эта конструкция основана на том, что |
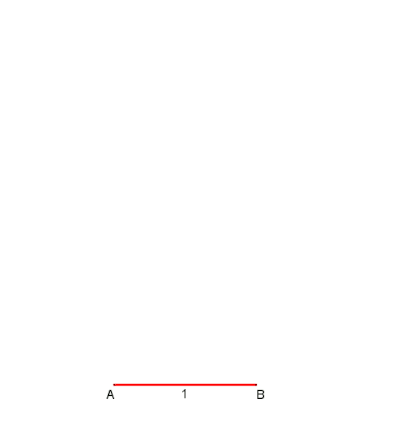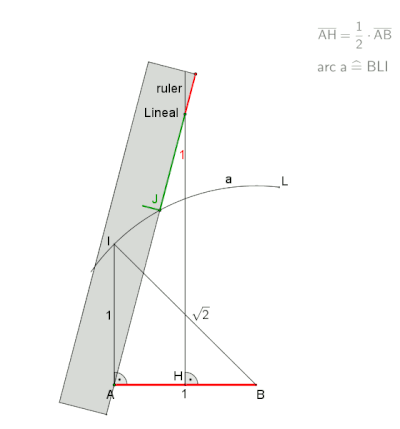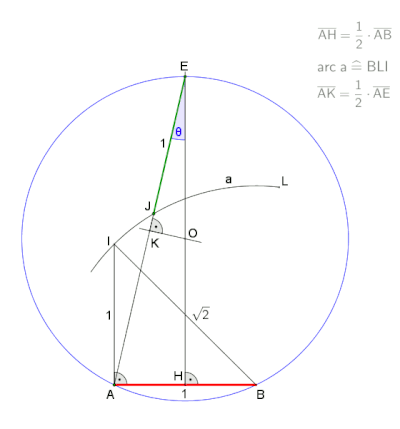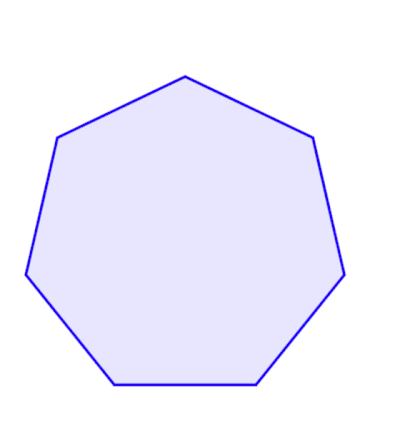
Анимация из конструкция Neusis с отмеченной линейкой, по словам Дэвида Джонсона Лейска (Крокетт Джонсон ),[2] пауза в конце 30 с.
Жерар т Хофт показывает правильный семиугольник, состоящий всего из 15 полосок Meccano с размером штанг 8 и 11.[3]

Конструкция состоит из двух равнобедренных треугольников, на которых закреплены остальные стержни. Сторона правильного семиугольника а, сторона более короткого равнобедренного треугольника е, а более длинная сторона равнобедренного треугольника d удовлетворить
Формула выводится из этого Семиугольный треугольник формула:
Небольшие возможные конструкции семиугольника:
| Семиугольник | а | d | е |
|---|---|---|---|
| 1 | 3 | 4 | 1 |
| 2 | 8 | 11 | 6 |
| 3 | 33 | 46 | 29 |
| 4 | 40 | 53 | 6 |
| 5 | 55 | 74 | 27 |
Самый маленький семиугольник конструктора 1: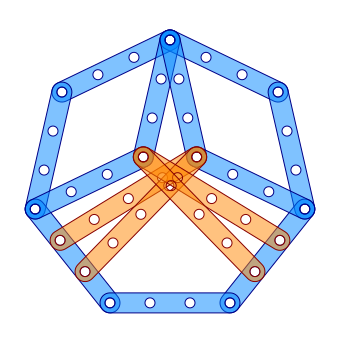
Приближение
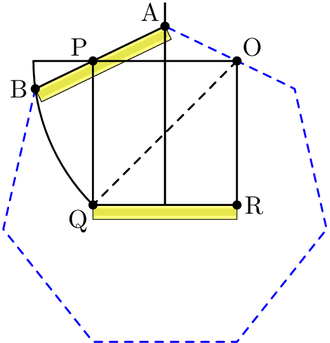
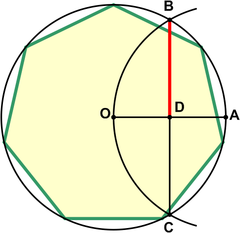
Примерное значение для практического использования с погрешностью около 0,2% показано на чертеже. Это приписывается Альбрехт Дюрер.[4] Позволять А лежат на окружности описанной окружности. Нарисуйте дугу BOC. потом дает приближение для края семиугольника.
Это приближение использует для стороны семиугольника, вписанной в единичный круг, а точное значение .
Пример для иллюстрации ошибки:
По радиусу описанной окружности r = 1 м, абсолютная погрешность 1-й стороны будет примерно -1,7 мм

Построение аппроксимации меккано может быть выполнено с одиннадцатью стержнями размером 20, 36 и 45. Эти значения оставляют ошибку около 0,1%.
Симметрия
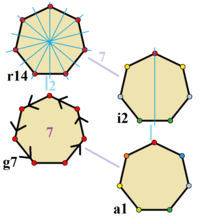
В правильный семиугольник принадлежит к D7ч точечная группа (Обозначение Шенфлиса ), порядок 28. Элементами симметрии являются: 7-кратная ось собственного вращения C7, 7-кратная неправильная ось вращения, S7, 7 вертикальных зеркальных плоскостей, σv, 7 осей 2-х кратного вращения, C2, в плоскости семиугольника и горизонтальной зеркальной плоскости σчас, также в плоскости семиугольника.[6]
Диагонали и семиугольный треугольник

Сторона правильного семиугольника а, короче диагональ б, и более длинная диагональ c, с а<б<cудовлетворить[7]:Лемма 1.
- (в оптическое уравнение )
и поэтому
и[7]:Коро. 2
Таким образом -б/c, c/а, и а/б все удовлетворяют кубическое уравнение Однако нет алгебраические выражения с чисто действительными членами существуют для решений этого уравнения, потому что это пример казус несокрушимый.
Приблизительная длина диагоналей относительно стороны правильного семиугольника определяется выражением
У нас также есть[8]
и
А семиугольный треугольник имеет вершины совпадающие с первой, второй и четвертой вершинами правильного семиугольника (из произвольной начальной вершины) и углами и Таким образом, его стороны совпадают с одной стороной и двумя частными диагонали правильного семиугольника.[7]
Звездные семиугольники
Два вида звездных семиугольников (гептаграммы ) можно построить из правильных семиугольников, помеченных Символы Шлефли {7/2} и {7/3} с делитель - интервал подключения.

Синие, {7/2} и зеленые {7/3} звездные семиугольники внутри красного семиугольника.
Эмпирические примеры

В настоящее время (2020 г.) Соединенное Королевство имеет две семиугольные монеты, то 50 пенсов и 20p штук, а Барбадос Доллар тоже семиугольный. В монете номиналом 20 евроцентов углубления размещены аналогично. Строго говоря, форма монет - это Семиугольник Reuleaux, а криволинейный семиугольник, чтобы сделать их кривые постоянной ширины: стороны изогнуты наружу, поэтому монета будет плавно катиться при вставке в торговый автомат. Ботсвана пула монеты достоинством 2 Пула, 1 Пула, 50 Фив и 5 Фив также имеют форму семиугольника равносторонней кривой. Монеты в форме семиугольника Рило также находятся в обращении на Маврикии, ОАЭ, Танзании, Самоа, Папуа-Новой Гвинее, Сан-Томе и Принсипи, Гаити, Ямайке, Либерии, Гане, Гамбии, Иордании, Джерси, Гернси, острове Мэн, Гибралтар, Гайана, Соломоновы острова, Фолклендские острова и остров Святой Елены. 1000 Квача Монета Замбии представляет собой настоящий семиугольник.
В Бразильский Монета достоинством 25 центов имеет семиугольник, вписанный в диск. Некоторые старые версии герб Грузии, в том числе в Советские времена, использовал гептаграмму {7/2} в качестве элемента.
В архитектуре семиугольные планы этажей встречаются очень редко. Замечательный пример - Мавзолей принца Эрнста в Stadthagen, Германия.
Многие полицейские значки в США имеют контур гептаграммы {7/2}.
Отдельно от семиугольная призма и семиугольная антипризма, ни один выпуклый многогранник, целиком состоящий из правильных многоугольников, не содержит семиугольника в качестве грани.
Обычные семиугольники могут выложить плитку гиперболическая плоскость, как показано в этом Модель диска Пуанкаре проекция:
Графики
K7 полный график часто рисуется как правильный семиугольник со всеми 21 ребром соединенными. Этот график также представляет собой орфографическая проекция из 7 вершин и 21 ребра 6-симплекс. В правильный косой многоугольник по периметру называется многоугольник петри.
 6-симплекс (6D) |
Гептагон в природе
Смотрите также
Рекомендации
- ^ а б Глисон, Эндрю Маттей (март 1988 г.). «Трехугольник, семиугольник и трехугольник стр. 186 (Рис.1) –187» (PDF). Американский математический ежемесячник. 95 (3): 185–194. Дои:10.2307/2323624. Архивировано из оригинал (PDF) 19 декабря 2015 г.
- ^ Вайсштейн, Эрик В. «Гептагон». Из MathWorld, веб-ресурса Wolfram.
- ^ Жерар т Хофт. "Meccano Mathematics I"
- ^ G.H. Хьюз, «Многоугольники Альбрехта Дюрера-1525, правильный семиугольник», рис. 11 сторона семиугольника (7) Рис. 15, изображение слева, получено 4 декабря 2015 г.
- ^ Джон Х. Конвей, Хайди Берджел, Хаим Гудман-Штраус, (2008) Симметрии вещей, ISBN 978-1-56881-220-5 (Глава 20, Обобщенные символы Шафли, Типы симметрии многоугольника, стр. 275-278)
- ^ Salthouse, J.A; Уэр, М.Дж. (1972). Таблицы знаков групп точек и связанные данные. Кембридж: Издательство Кембриджского университета. ISBN 0 521 08139 4.
- ^ а б c Абдилкадир Алтынтас, "Некоторые коллинеарности в семиугольном треугольнике", Форум Geometricorum 16, 2016, 249–256.http://forumgeom.fau.edu/FG2016volume16/FG201630.pdf
- ^ Леон Банкофф и Джек Гарфанкел, «Семигранный треугольник», Математический журнал 46 (1), январь 1973 г., 7–19.
внешняя ссылка
- Определение и свойства семиугольника С интерактивной анимацией
- Гептагон по Джонсону
- Еще один примерный способ строительства
- Полигоны - семиугольники
- Недавно открытое и очень точное приближение для построения правильного семиугольника.
- Гептагон, приближенная конструкция в виде анимации
- Семиугольник с заданной стороной, приближенная конструкция в виде анимации




![{ displaystyle A = { frac {a ^ {2}} {4}} { sqrt {{ frac {7} {3}} left (35 + 2 { sqrt [{3}] {196}) } left ({ sqrt [{3}] {13-3i { sqrt {3}}}} + { sqrt [{3}] {13 + 3i { sqrt {3}}}} right) верно)}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ee4a0e485c1fd2ddbeb7141f8eef064a997f70e5)




























