Кубическая функция - Cubic function

График кубической функции с 3 настоящий корни (где кривая пересекает горизонтальную ось - где у = 0). Показанный чехол имеет два критические точки. Здесь функция ж(Икс) = (Икс³ + 3Икс² − 6Икс − 8)/4.

В математика, а кубическая функция это функция формы

${ displaystyle f (x) = ax ^ {3} + bx ^ {2} + cx + d}$

где коэффициенты а, б, c, и d находятся действительные числа, а переменная Икс принимает реальные значения, и а ≠ 0. Другими словами, это одновременно полиномиальная функция степени три, и реальная функция. В частности, домен и codomain представляют собой набор действительных чисел.

Параметр ж(Икс) = 0 производит кубическое уравнение формы

${ displaystyle ax ^ {3} + bx ^ {2} + cx + d = 0,}$

чьи решения называются корни функции.

Кубическая функция имеет один или три действительных корня;^[1] все многочлены нечетной степени имеют хотя бы один действительный корень.

В график кубической функции всегда имеет единственный точка перегиба. Может быть два критические точки, локальный минимум и локальный максимум. В противном случае кубическая функция монотонный. График кубической функции симметричен относительно точки перегиба; то есть, он инвариантен относительно поворота на пол-оборота вокруг этой точки. Вплоть до ан аффинное преобразование, есть только три возможных графика для кубических функций.

Кубические функции являются фундаментальными для кубическая интерполяция.

История

Критические и переломные моменты

В корни, стационарные точки, точка перегиба и вогнутость из кубический многочлен Икс³ − 3Икс² − 144Икс + 432 (черная линия) и его первая и вторая производные (красный и синий).

В критические точки кубической функции являются ее стационарные точки, то есть точки, в которых наклон функции равен нулю.^[2] Таким образом, критические точки кубической функции ж определяется

ж(Икс) = топор³ + bx² + сх + d,

происходят при значениях Икс так что производная

${ displaystyle 3ax ^ {2} + 2bx + c = 0}$

кубической функции равна нулю.

Решениями этого уравнения являются Икс-значения критических точек и даны с использованием квадратичная формула, к

${ displaystyle x _ { text {critical}} = { frac {-b pm { sqrt {b ^ {2} -3ac}}} {3a}}.}$

Знак выражения внутри квадратного корня определяет количество критических точек. Если он положительный, то есть две критические точки, одна - локальный максимум, а другая - локальный минимум. Если б² – 3ac = 0, то есть только одна критическая точка - точка перегиба. Если б² – 3ac < 0, то (реальных) критических точек нет. В двух последних случаях, т. Е. Если б² – 3ac неположительна, кубическая функция строго монотонный. См. Рисунок для примера корпуса Δ₀ > 0.

Точка перегиба функции - это место, где она изменяется вогнутость.^[3] Точка перегиба возникает, когда вторая производная ${ displaystyle f '' (x) = 6ax + 2b,}$ равна нулю, а третья производная отлична от нуля. Таким образом, кубическая функция всегда имеет одну точку перегиба, которая встречается в

${ displaystyle x _ { text {inflection}} = - { frac {b} {3a}}.}$

Классификация

Кубические функции формы ${ displaystyle y = x ^ {3} + px.}$
График любой кубической функции есть похожий к такой кривой.

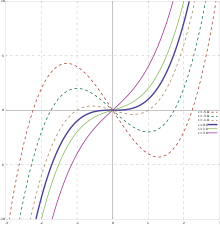
В график кубической функции является кубическая кривая, хотя многие кубические кривые не являются графиками функций.

Хотя кубические функции зависят от четырех параметров, их график может иметь очень мало форм. На самом деле график кубической функции всегда похожий графику функции вида

${ displaystyle y = x ^ {3} + px.}$

Это сходство можно построить как композицию переводы параллельно осям координат, a гомотия (равномерное масштабирование ), и, возможно, отражение (зеркальное изображение ) с уважением к у-ось. Дальше неравномерное масштабирование может преобразовать график в график одной из трех кубических функций

${ displaystyle { begin {align} y & = x ^ {3} + x y & = x ^ {3} y & = x ^ {3} -x. end {выравнивается}}}$

Это означает, что есть только три графика кубических функций вплоть до ан аффинное преобразование.

Вышесказанное геометрические преобразования можно построить следующим образом, исходя из общей кубической функции ${ displaystyle y = ax ^ {3} + bx ^ {2} + cx + d.}$

Во-первых, если а < 0, то изменение переменной Икс → –Икс позволяет предположить а > 0. После этой замены переменной новый график является зеркальным отображением предыдущего по отношению к у-ось.

Тогда замена переменной Икс = Икс₁ – б/3а предоставляет функцию формы

${ displaystyle y = ax_ {1} ^ {3} + px_ {1} + q.}$

Это соответствует переносу, параллельному Икс-ось.

Изменение переменной у = у₁ + q соответствует переводу относительно у-оси, и дает функцию вида

${ displaystyle y_ {1} = ax_ {1} ^ {3} + px_ {1}.}$

Изменение переменной ${ displaystyle textstyle x_ {1} = { frac {x_ {2}} { sqrt {a}}}, y_ {1} = { frac {y_ {2}} { sqrt {a}}} }$ соответствует равномерному масштабированию и дают после умножения на ${ displaystyle { sqrt {a}},}$ функция формы

${ displaystyle y_ {2} = x_ {2} ^ {3} + px_ {2},}$

что является самой простой формой, которую можно получить подобием.

Тогда, если п ≠ 0, неравномерное масштабирование ${ displaystyle textstyle x_ {2} = x_ {3} { sqrt {| p |}}, quad y_ {2} = y_ {3} { sqrt {| p | ^ {3}}}}$ дает после деления на ${ displaystyle textstyle { sqrt {| p | ^ {3}}},}$

${ displaystyle y_ {3} = x_ {3} ^ {3} + x_ {3} operatorname {sign} (p),}$

куда ${ displaystyle operatorname {знак} (p)}$ имеет значение 1 или –1, в зависимости от знака п. Если определить ${ displaystyle operatorname {sign} (0) = 0,}$ последняя форма функции применяется ко всем случаям (с ${ displaystyle x_ {2} = x_ {3}}$ и ${ displaystyle y_ {2} = y_ {3}}$).

Симметрия

Для кубической функции вида ${ displaystyle y = x ^ {3} + px,}$ точка перегиба, таким образом, является началом координат. Таким образом, функция является нечетная функция, его график симметричен относительно точки перегиба и инвариантен относительно поворота на пол-оборота вокруг точки перегиба. Поскольку эти свойства инвариантны сходство, для всех кубических функций верно следующее.

График кубической функции симметричен относительно точки перегиба и инвариантен при повороте на пол-оборота вокруг точки перегиба.

Коллинеарности

Точки п₁, п₂, и п₃ (синим цветом) коллинеарны и принадлежат графику Икс³ + 3/2Икс² − 5/2Икс + 5/4. Точки Т₁, Т₂, и Т₃ (красным) - точки пересечения (пунктирных) касательных к графику в этих точках с самим графиком. Они тоже коллинеарны.

Касательные к графику кубической функции в трех точках коллинеарные точки снова перехватить кубику в коллинеарных точках.^[4] Это можно увидеть следующим образом.

Поскольку это свойство инвариантно относительно жесткое движение, можно предположить, что функция имеет вид

${ displaystyle f (x) = x ^ {3} + px.}$

Если α действительное число, то касательная к графику ж в момент (α, ж(α)) это линия

{(Икс, ж(α) + (Икс − α)ж ′(α)) : Икс ∈ р}.

Итак, точка пересечения этой линии и графика ж можно получить, решив уравнение ж(Икс) = ж(α) + (Икс − α)ж ′(α), то есть

${ displaystyle x ^ {3} + px = alpha ^ {3} + p alpha + (x- alpha) (3 alpha ^ {2} + p),}$

который можно переписать

${ displaystyle x ^ {3} -3 alpha ^ {2} x + 2 alpha ^ {3} = 0,}$

и разложен на множители как

${ Displaystyle (х- альфа) ^ {2} (х + 2 альфа) = 0.}$

Итак, касательная пересекает кубику в точке

${ displaystyle (-2 alpha, -8 alpha ^ {3} -2p alpha) = (- 2 alpha, -8f ( alpha) -10p alpha).}$

Итак, функция, отображающая точку (Икс, у) графика в другую точку, где касательная пересекает график,

${ displaystyle (x, y) mapsto (-2x, -8y-10px).}$

Это аффинное преобразование который преобразует коллинеарные точки в коллинеарные точки. Это подтверждает заявленный результат.

Кубическая интерполяция

Учитывая значения функции и ее производной в двух точках, существует ровно одна кубическая функция, которая имеет те же четыре значения, которая называется кубический шлиц Эрмита.

Есть два стандартных способа использовать этот факт. Во-первых, если кто-то знает, например, путем физического измерения значения функции и ее производной в некоторых точках выборки, можно интерполировать функция с непрерывно дифференцируемая функция, что является кусочно кубическая функция.

Если значение функции известно в нескольких точках, кубическая интерполяция состоит в приближении функции непрерывно дифференцируемая функция, который кусочно кубический. Чтобы иметь однозначно определенную интерполяцию, необходимо добавить еще два ограничения, например, значения производных в конечных точках или нулевое значение. кривизна в конечных точках.

Ссылка

внешняя ссылка

• «Формула Кардано», Энциклопедия математики, EMS Press, 2001 [1994]
• История квадратных, кубических и четвертых уравнений на Архив MacTutor.