Строительство Neusis - Neusis construction

Строительство Neusis

В Neusis (от греч. νεῦσις от νεύειν neuein "склоняться к"; множественное число: νεύσεις Neuseis) - геометрический метод построения, который использовался в древности греческими математиками.

Геометрическая конструкция

Конструкция neusis состоит из подгонки линейного элемента заданной длины (а) между двумя заданными строками (л и м) таким образом, что элемент линии или его продолжение проходит через заданную точку п. То есть один конец линейного элемента должен лежать на л, другой конец на м, а линейный элемент «наклонен» к п.

Точка п называется полюсом неусиса, линия л директриса, или направляющая линия, и линия м линия захвата. Длина а называется диастема (διάστημα; по-гречески «расстояние»).

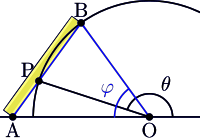
Построение neusis может быть выполнено с помощью «линейки neusis»: отмеченной линейки, которая может вращаться вокруг точки. п (это можно сделать, вставив булавку в острие п а затем прижав линейку к штифту). На рисунке один конец линейки отмечен желтым глазком с перекрестием: отсюда деление шкалы на линейке. Вторая отметка на линейке (синий глаз) указывает расстояние а от происхождения. Желтый глаз перемещается по линии л, пока синий глаз не совпадет с линией м. Положение найденного таким образом линейного элемента показано на рисунке в виде темно-синей полосы.

Трисекция угла по Нейзису θ > 135 °, чтобы найти φ = θ/ 3, используя только длину линейки. Радиус дуги равен длине линейки. Для углов θ <135 ° применяется та же конструкция, но с P, выходящим за пределы AB.

Использование neusis

Neuseis были важны, потому что они иногда предоставляют средства для решения геометрических задач, которые нельзя решить с помощью компас и линейка один. Примерами являются трисекция любого угла в трех равных частях удвоение куба, а строительство регулярного семиугольник, девятиугольник, или же трехугольник (полигоны с 7, 9 или 13 сторонами).[1] Математики, такие как Архимед Сиракуз (287–212 до н. э.) и Папп Александрийский (290-350 гг. Н.э.) свободно использовались Neuseis; сэр Исаак Ньютон (1642-1726) следовали их мышлению и также использовали конструкции neusis.[2] Тем не менее постепенно методика вышла из употребления.

Обычный п-gon, как известно, можно построить с помощью neusis для п =

3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 24, 26, 27, 28, 30, 32, 33, 34, 35, 36, 37, 38, 39, 40, 42, 44, 45, 48, 51, 52, 54, 55, 56, 57, 60, 63, 64, 65, 66, 68, 70, 72, 73, 74, 76, 77, 78, 80, 81, 84, 85, 88, 90, 91, 95, 96, 97, 99, 102, 104, 105, 108, 109, 110, 111, 112, 114, 117, 119, 120, 126, 128, ... (последовательность A122254 в OEIS ), измененный недавним открытием Бенджамина и Снайдера, что обычный девичник неузис-конструируемый,[3]

в то время как регулярный п-gon, как известно, не может быть построен с помощью neusis для п =

23, 29, 43, 46, 47, 49, 53, 58, 59, 67, 69, 71, 79, 83, 86, 87, 89, 92, 94, 98, 103, 106, 107, 113, 115, 116, 118, 121, 127, ... (последовательность A048136 в OEIS ), модифицированный аналогично.

со статусом все еще открытый вопрос для п =

25, 31, 41, 50, 61, 62, 75, 82, 93, 100, 101, 122, 123, 124, 125, ...

Падение популярности

Т. Л. Хит, историк математики, предположил, что греческий математик Энопид (ок. 440 г. до н.э.) был первым, кто поместил конструкции из циркуля и линейки над Neuseis. Принцип избегать Neuseis по возможности мог быть распространен Гиппократ Хиосский (ок. 430 г. до н.э.), который происходил с того же острова, что и Энопид, и который, насколько нам известно, был первым, кто написал систематически упорядоченный учебник геометрии. Через сто лет после него Евклид слишком избегаемый Neuseis в его очень влиятельном учебнике, Элементы.

Следующая атака на невзис произошла, когда с четвертого века до нашей эры Платон с идеализм набрал силу. Под его влиянием сложилась иерархия из трех классов геометрических построений. Переходя от «абстрактного и благородного» к «механическому и земному», эти три класса были:

  1. конструкции только с прямыми и окружностями (циркуль и линейка);
  2. конструкции, в которых кроме этого используются конические сечения (эллипсы, параболы, гиперболы );
  3. конструкции, которые нуждались в других средствах строительства, например Neuseis.

В конце концов, использование neusis было сочтено приемлемым только тогда, когда две другие, более высокие категории конструкций не предложили решения. Neusis стал своего рода последним средством, которое использовалось только тогда, когда все другие, более респектабельные методы потерпели неудачу. Использование neusis там, где могли быть использованы другие методы построения, было заклеймено позднегреческим математиком. Папп Александрийский (ок. 325 г.) как «немалую ошибку».

Смотрите также

Рекомендации

  1. ^ Вайсштейн, Эрик В. «Neusis Construction». Материал из MathWorld - веб-ресурса Wolfram. http://mathworld.wolfram.com/NeusisConstruction.html
  2. ^ Гвиччардини, Никколо (2009). Исаак Ньютон о математической достоверности и методе, выпуск 4. M.I.T Press. п. 68. ISBN  9780262013178.
  3. ^ Бенджамин, Эллиот; Снайдер, К. (май 2014 г.). «О построении правильного пятиугольника с помощью линейки и циркуля». Математические труды Кембриджского философского общества. 156 (3): 409–424. Дои:10.1017 / S0305004113000753. В архиве с оригинала 26 сентября 2020 г.. Получено 26 сентября 2020.
  • Р. Бёкер, «Neusis», в: Paulys Realencyclopädie der Classischen Altertumswissenschaft, G. Wissowa red. (1894–), Дополнение 9 (1962) 415–461. – На немецком языке. Самый полный обзор; однако у автора иногда возникают довольно любопытные мнения.
  • Т. Л. Хит, История греческой математики (2 тома; Оксфорд 1921).
  • Х. Г. Цойтен, Die Lehre von den Kegelschnitten im Altertum [= Теория конических сечений в древности] (Копенгаген, 1886 г .; перепечатано в Хильдесхайме, 1966 г.).

внешняя ссылка