Конструкция линейки и компаса - Википедия - Straightedge and compass construction

Создание регулярного шестиугольник с линейкой и компасом

Геометрия
Проектирование а сфера к самолет
Контур История
ветви Евклидово Неевклидово Эллиптический Сферический Гиперболический Неархимедова геометрия Проективный Аффинный Синтетический Аналитический Алгебраический Арифметика Диофантин Дифференциальный Риманов Симплектический Дискретный дифференциал Сложный Конечный Дискретный / Комбинаторный Цифровой Выпуклый Вычислительная Фрактал Заболеваемость
Концепции Функции Измерение Конструкции линейки и компаса Угол Изгиб Диагональ Ортогональность (Перпендикуляр ) Параллельный Вершина Конгруэнтность Сходство Симметрия
Нульмерный Точка
Одномерный Линия сегмент луч Длина
Двумерный Самолет Площадь Многоугольник Треугольник Высота Гипотенуза теорема Пифагора Параллелограмм Квадрат Прямоугольник Ромб Ромбовидный Четырехугольник Трапеция летающий змей Круг Диаметр Длина окружности Площадь
Трехмерный Объем Куб кубовид Цилиндр Пирамида Сфера
Четыре - / другое измерение Тессеракт Гиперсфера
Геометры
по имени Аида Арьябхата Ахмес Альхазен Аполлоний Архимед Атья Баудхаяна Бойяи Брахмагупта Картан Coxeter Декарт Евклид Эйлер Гаусс Громов Гильберта Джиешхадева Катьяяна Хайям Кляйн Лобачевский Манава Минковский Минггату Паскаль Пифагор Парамешвара Пуанкаре Риман Сакабэ Sijzi ат-Туси Веблен Вирасена Ян Хуэй аль-Ясамин Чжан Список геометров
по периоду До н.э. Ахмес Баудхаяна Манава Пифагор Евклид Архимед Аполлоний 1–1400 Чжан Катьяяна Арьябхата Брахмагупта Вирасена Альхазен Sijzi Хайям аль-Ясамин ат-Туси Ян Хуэй Парамешвара 1400–1700 гг. Джиешхадева Декарт Паскаль Минггату Эйлер Сакабэ Аида 1700–1900-е гг. Гаусс Лобачевский Бойяи Риман Кляйн Пуанкаре Гильберта Минковский Картан Веблен Coxeter Сегодняшний день Атья Громов

Конструкция линейки и компаса, также известный как линейка-компас или же классическая конструкция, - построение длин, углы, и другие геометрические фигуры, используя только идеализированный линейка и компас.

Идеализированный правитель, известный как прямая грань, предполагается иметь бесконечную длину, иметь только одну кромку и без маркировки на ней. Предполагается, что у компаса нет максимального или минимального радиуса, и предполагается, что компас «схлопывается» при поднятии со страницы, поэтому его нельзя напрямую использовать для переноса расстояний. (Это неважное ограничение, поскольку, используя многоступенчатую процедуру, расстояние можно передать даже с помощью сворачивающегося компаса; см. компас теорема эквивалентности.) Более формально, единственно допустимые конструкции - это те, которые предоставлены Евклид первые три постулаты.

Оказывается, каждая точка может быть построена с помощью линейки и циркуля. также могут быть построены с использованием только компаса.

В древнегреческие математики впервые задумал конструкции линейки и компаса, а также ряд древних проблем в плоская геометрия наложить это ограничение. Древние греки разработали множество построек, но в некоторых случаях не смогли этого сделать. Гаусс показал, что некоторые полигоны конструктивны, но большинство из них - нет. Некоторые из самых известных задач с линейкой и компасом оказались невозможными. Пьер Ванцель в 1837 г., используя математическую теория полей.

Несмотря на существующие доказательства невозможности, Некоторые упорно пытаются решить эти проблемы.^[1] Многие из этих проблем легко решаются при условии, что разрешены другие геометрические преобразования: например, удвоение куба можно использовать геометрические конструкции, но нельзя использовать только линейку и циркуль.

С точки зрения алгебра, длина конструктивна если и только если он представляет собой конструктивное число, а угол конструктивен тогда и только тогда, когда его косинус конструктивное число. Число можно построить тогда и только тогда, когда оно может быть записано с использованием четырех основных арифметических операций и извлечения квадратные корни но не корней высшего порядка.

Инструменты линейки и компаса

Линейка и компас

Компас

«Линейка» и «циркуль» в конструкциях линейки и компаса - это идеализации линейок и циркулей в реальном мире:

• В прямая грань бесконечно длинная, но на ней нет маркировки и только одна прямая кромка, в отличие от обычных линейок. Его можно использовать только для рисования отрезка между двумя точками или для удлинения существующего отрезка.
• В компас может открываться сколь угодно широко, но (в отличие от некоторых реальных компасы ) на нем нет маркировки. Круги можно нарисовать только из двух заданных точек: центра и точки на окружности. Компас может или не может сломаться, когда он не рисует круг.

Настоящие компасы не разрушаются, и современные геометрические конструкции часто используют эту функцию. «Коллапсирующий компас» может показаться менее мощным инструментом. компас теорема эквивалентности в предложении 2 книги 1 Элементы Евклида, никакая сила не теряется при использовании рушащегося компаса. Хотя утверждение верно, его доказательства имеют долгую и неоднозначную историю.^[2]

Каждая конструкция должна быть точный. «Наблюдать» за ним (по сути, смотреть на конструкцию и угадывать ее точность или использовать какую-либо форму измерения, например, единицы измерения на линейке) и приближение не считается решением.

Каждая конструкция должна прекратить. То есть он должен иметь конечное число шагов, а не быть пределом все более близких приближений.

Таким образом, линейка и компас выглядят как салонная игра, а не серьезная практическая проблема; но цель ограничения - гарантировать, что конструкции могут быть доказано быть точно правильный.

История

В древнегреческие математики сначала попытались построить линейку и циркуль, и они обнаружили, как строить суммы, разности, произведения, отношения и квадратные корни заданной длины.^{[3]:п. 1} Они также могли построить половина заданного угла, квадрат, площадь которого вдвое больше, чем у другого квадрата, квадрат, имеющий такую ​​же площадь, что и данный многоугольник, и правильный многоугольник с 3, 4 или 5 сторонами^{[3]:п. xi} (или один с удвоенным количеством сторон данного многоугольника^{[3]:стр. 49–50}). Но они не могли построить одну треть заданного угла, кроме особых случаев, или квадрат с той же площадью, что и данный круг, или правильный многоугольник с другим числом сторон.^{[3]:п. xi} Также они не могли построить сторону куба, объем которой был бы вдвое больше объема куба с данной стороной.^{[3]:п. 29}

Гиппократ и Менахм показали, что объем куба можно увеличить вдвое, найдя пересечения гиперболы и параболы, но их нельзя построить с помощью линейки и компаса.^{[3]:п. 30} В пятом веке до нашей эры Гиппий использовал кривую, которую он назвал квадратик чтобы разрезать общий угол и возвести круг в квадрат, и Никомед во втором веке до нашей эры показали, как использовать раковина разрезать произвольный угол;^{[3]:п. 37} но этим методам также нельзя следовать с помощью линейки и циркуля.

Никакого прогресса в решении нерешенных проблем не было на протяжении двух тысячелетий, до 1796 года. Гаусс показал, что можно построить правильный многоугольник с 17 сторонами; пять лет спустя он показал достаточный критерий правильного многоугольника п стороны должны быть конструктивными.^{[3]:стр. 51 и сл.}

В 1837 г. Пьер Ванцель опубликовал доказательство невозможности разрезания произвольного угла на три части или удвоения объема куба,^[4] по причине невозможности строительства кубические корни длин. Он также показал, что достаточное условие конструктивности Гаусса для правильных многоугольников также необходимо.^[5]

Затем в 1882 г. Lindemann показало, что ${ displaystyle pi}$ это трансцендентное число, и, таким образом, с помощью линейки и циркуля невозможно построить квадрат с той же площадью, что и данный круг.^{[3]:п. 47}

Основные конструкции

Основные конструкции

Все построения линейки и циркуля состоят из многократного применения пяти основных построений с использованием уже построенных точек, линий и окружностей. Это:

• Создание линии через две существующие точки
• Создание круга через одну точку с центром в другой точке
• Создание точки, являющейся пересечением двух существующих непараллельных линий
• Создание одной или двух точек на пересечении прямой и окружности (если они пересекаются)
• Создание одной или двух точек на пересечении двух окружностей (если они пересекаются).

Например, начав всего с двух различных точек, мы можем создать линию или любой из двух кругов (в свою очередь, используя каждую точку как центр и проходя через другую точку). Если мы нарисуем оба круга, на их пересечении будут созданы две новые точки. Проведение линий между двумя исходными точками и одной из этих новых точек завершает построение равностороннего треугольника.

Следовательно, в любой геометрической задаче у нас есть исходный набор символов (точек и линий), алгоритм и некоторые результаты. С этой точки зрения геометрия эквивалентна аксиоматике. алгебра, заменяя его элементы символами. Наверное Гаусс впервые осознал это и использовал это, чтобы доказать невозможность некоторых конструкций; только намного позже Гильберта найти полный набор аксиомы геометрии.

Часто используемые линейки и компасные конструкции

К наиболее часто используемым конструкциям линейки и компаса относятся:

• Строительство серединный перпендикуляр из сегмента
• Нахождение середина сегмента.
• Рисование перпендикулярная линия от точки до линии.
• Деление угла пополам
• Зеркальное отображение точки на линии
• Построение прямой через точку, касательную к окружности
• Построение круга через 3 неколлинеарные точки
• Проведение линии через заданную точку параллельно заданной линии.

Конструируемые точки и длины

Конструкции линейки и циркуля, соответствующие алгебраическим операциям
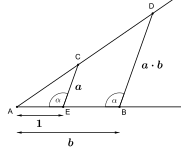Икс=а·б (теорема о перехвате)	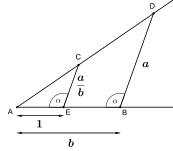Икс=а/б (теорема о перехвате)	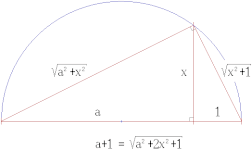Икс=√а (Теорема Пифагора)

Многое из того, что можно построить, описано в теорема о перехвате к Фалес.

Мы могли бы связать алгебру с нашей геометрией, используя Декартова система координат состоящий из двух линий, и представляют точки нашей плоскости векторов. Наконец, мы можем записать эти векторы в виде комплексных чисел.

Используя уравнения для прямых и окружностей, можно показать, что точки, в которых они пересекаются, лежат в квадратичное расширение самого маленького поля F содержащий две точки на прямой, центр круга и радиус круга. То есть они имеют вид Икс +у√k, куда Икс, у, и k находятся в F.

Поскольку поле конструктивных точек замкнуто относительно квадратные корни, он содержит все точки, которые могут быть получены конечной последовательностью квадратичных расширений поля комплексных чисел с рациональными коэффициентами. С помощью приведенного выше абзаца можно показать, что любая конструктивная точка может быть получена такой последовательностью расширений. Как следствие этого, можно найти, что степень минимального многочлена для конструктивной точки (и, следовательно, любой конструктивной длины) равна степени 2. В частности, любая конструктивная точка (или длина) является алгебраическое число, хотя не всякое алгебраическое число конструктивно; Например, ³√2 алгебраичен, но не конструктивен.^[4]

Конструируемые углы

Существует биекция между углами, которые можно построить, и точками, которые можно построить, на любой конструктивной окружности. Углы, которые можно построить, образуют абелева группа при сложении по модулю 2π (что соответствует умножению точек на единичной окружности, рассматриваемой как комплексные числа). Конструируемые углы - это именно те углы, тангенс которых (или, что то же самое, синус или косинус) может быть сконструирован как число. Например, обычный гептадекагон (семнадцатигранный правильный многоугольник ) конструктивно, потому что

${ displaystyle cos { left ({ frac {2 pi} {17}} right)} = - { frac {1} {16}} ; + ; { frac {1} {16 }} { sqrt {17}} ; + ; { frac {1} {16}} { sqrt {34-2 { sqrt {17}}}} ; + ; { frac {1 } {8}} { sqrt {17 + 3 { sqrt {17}} - { sqrt {34-2 { sqrt {17}}}} - 2 { sqrt {34 + 2 { sqrt {17 }}}}}}}$

как обнаружено Гаусс.^[6]

Группа конструктивных углов замыкается операцией деления углов пополам (что соответствует извлечению квадратного корня из комплексных чисел). Единственные углы конечного порядка, которые могут быть построены, начиная с двух точек, - это углы, порядок которых является либо степенью двойки, либо произведением степени двойки и множества различных Простые числа Ферма. Вдобавок существует плотный набор конструктивных углов бесконечного порядка.

Конструкции линейки и циркуля как сложная арифметика

Учитывая набор точек в Евклидова плоскость, выбирая любой из них для вызова 0 и еще один будет называться 1, вместе с произвольным выбором ориентация позволяет рассматривать точки как набор сложные числа.

При любой такой интерпретации набора точек как комплексных чисел, точки, которые можно построить с использованием только правильных построений линейки и компаса, являются в точности элементами наименьшего поле содержащий исходный набор точек и закрытый под комплексно сопряженный и квадратный корень операций (чтобы избежать неоднозначности, мы можем указать квадратный корень с сложный аргумент меньше π). Элементы этого поля - это именно те элементы, которые могут быть выражены в виде формулы в исходных точках, используя только операции добавление, вычитание, умножение, разделение, комплексно сопряженный, и квадратный корень, которое, как легко видеть, является счетным плотным подмножеством плоскости. Каждая из этих шести операций соответствует простой конструкции линейки и циркуля. По такой формуле легко произвести построение соответствующей точки, комбинируя конструкции для каждой из арифметических операций. Более эффективное построение определенного набора точек соответствует сокращению в таких расчетах.

Эквивалентным образом (и без необходимости произвольно выбирать две точки) мы можем сказать, что при произвольном выборе ориентации набор точек определяет набор комплексных соотношений, задаваемых отношениями разностей между любыми двумя парами точек. Набор соотношений, который можно построить с помощью линейки и циркуля из такого набора соотношений, является в точности наименьшим полем, содержащим исходные соотношения и замкнутым при взятии комплексных сопряжений и квадратных корней.

Например, действительная часть, мнимая часть и модуль точки или отношения z (принимая одну из двух точек зрения, приведенных выше) конструктивны, поскольку они могут быть выражены как

${ displaystyle mathrm {Re} (z) = { frac {z + { bar {z}}} {2}} ;}$

${ displaystyle mathrm {Im} (z) = { frac {z - { bar {z}}} {2i}} ;}$

${ displaystyle left | z right | = { sqrt {z { bar {z}}}}. ;}$

Удвоение куба и трисечение угла (кроме особых углов, таких как любой φ такой, что φ/ 2π является Рациональное число с знаменатель не делится на 3) требуются соотношения, которые являются решением кубические уравнения, пока квадрат круга требует трансцендентный соотношение. Ни один из них не входит в описанные поля, поэтому для них не существует линейки и компаса.

Невозможные конструкции

Древние греки думали, что проблемы строительства, которые они не могли решить, были просто упрямыми, а не неразрешимыми.^[7] Однако с помощью современных методов эти конструкции линейки и циркуля оказались логически невозможными. (Однако сами проблемы разрешимы, и греки знали, как их решать, не ограничиваясь работой только с линейкой и компасом.)

Квадрат круга

Самая известная из этих проблем, квадрат круга, иначе известная как квадратура круга, включает построение квадрата с той же площадью, что и данный круг, с использованием только линейки и циркуля.

Было доказано, что возведение круга в квадрат невозможно, поскольку оно предполагает создание трансцендентное число, то есть, √π. Только определенные алгебраические числа могут быть построены только с помощью линейки и циркуля, а именно построены из целых чисел с конечной последовательностью операций сложения, вычитания, умножения, деления и извлечения квадратных корней. По этой причине фраза «квадрат круга» часто используется для обозначения «невозможного».

Без ограничения, требующего решения только с помощью линейки и циркуля, проблема легко решается с помощью самых разных геометрических и алгебраических средств, и в древности она решалась много раз.^[8]

Метод, очень близкий к аппроксимации "квадратуры круга", может быть достигнут с использованием Треугольник Кеплера.

Удвоение куба

Удвоение куба - это построение с использованием только линейки и циркуля ребра куба, который имеет вдвое больший объем, чем куб с данным ребром. Это невозможно, потому что кубический корень из 2, хотя и является алгебраическим, не может быть вычислен из целых чисел сложением, вычитанием, умножением, делением и извлечением квадратных корней. Это следует потому, что его минимальный многочлен над рациональными числами имеет степень 3. Это построение возможно с помощью линейки с двумя отметками на ней и циркуля.

Трисекция угла

Трисекция угла - это построение с использованием только линейки и циркуля угла, который составляет одну треть заданного произвольного угла. В общем случае это невозможно. Например, угол 2π / 5 радианы (72 ° = 360 ° / 5) можно разрезать пополам, но угол π / 3 радианы (60° ) нельзя разделить на три части.^[9] Общая проблема трисекции также легко решается, когда линейка с двумя отметками на ней разрешена (a Neusis строительство).

Расстояние до эллипса

Отрезок от любой точки на плоскости до ближайшей точки на круг можно построить, но отрезок от любой точки на плоскости до ближайшей точки на эллипс положительных эксцентриситет вообще не могут быть построены.^[10]

Проблема Альхазена

В 1997 г. Оксфорд математик Питер М. Нойман доказал теорему о том, что не существует линейки и циркуля для общего решения древних Проблема Альхазена (бильярдная задача или отражение от сферического зеркала).^[11][12]

Построение правильных многоугольников

Строительство регулярного пятиугольник

Немного правильные многоугольники (например, пятиугольник ) легко построить с помощью линейки и циркуля; другие нет. Это привело к вопросу: можно ли построить все правильные многоугольники с помощью линейки и циркуля?

Карл Фридрих Гаусс в 1796 г. показал, что можно построить правильный 17-сторонний многоугольник, а пять лет спустя показал, что правильный п-сторонний многоугольник можно построить с помощью линейки и циркуля, если нечетное главные факторы из п отличны Простые числа Ферма. Гаусс предполагаемый что это условие также было необходимо, но он не представил доказательств этого факта, которые были представлены Пьер Ванцель в 1837 г.^[5]

Первые несколько конструктивных правильных многоугольников имеют следующее количество сторон:

3, 4, 5, 6, 8, 10, 12, 15, 16, 17, 20, 24, 30, 32, 34, 40, 48, 51, 60, 64, 68, 80, 85, 96, 102, 120, 128, 136, 160, 170, 192, 204, 240, 255, 256, 257, 272 ... (последовательность A003401 в OEIS )

Известно, что существует бесконечное множество конструктивных правильных многоугольников с четным числом сторон (потому что если правильный п-gon конструктивно, то и обычный 2п-угольник и, следовательно, правильный 4п-угольник, 8п-гон и др.). Однако существует только 31 известный конструктивный регулярный п-угольники с нечетным числом сторон.

Построение треугольника из трех заданных характерных точек или длин

Шестнадцать ключевых моментов треугольник это его вершины, то середины его сторон, ноги его высоты, ноги его биссектриса внутреннего угла, и это центр окружности, центроид, ортоцентр, и стимулятор. Их можно брать по три за раз, чтобы получить 139 различных нетривиальных задач построения треугольника из трех точек.^[13] Из этих проблем три связаны с точкой, которую можно однозначно построить из двух других точек; 23 может быть построено не однозначно (фактически, для бесконечного числа решений), но только в том случае, если положения точек подчиняются определенным ограничениям; в 74 задача в общем случае конструктивна; а в 39 требуемый треугольник существует, но не может быть построен.

Двенадцать ключевых длин треугольника - это три стороны, три высоты, три медианы, а три биссектриса угла. Вместе с тремя углами они дают 95 различных комбинаций, 63 из которых образуют конструктивный треугольник, 30 из которых нет, а два из которых не определены.^{[14]:стр. 201–203}

Ограниченные конструкции

Были предприняты различные попытки ограничить допустимые инструменты для конструкций в соответствии с различными правилами, чтобы определить, что еще можно построить и как это может быть построено, а также определить минимальные критерии, необходимые для того, чтобы все еще можно было построить все, что компас и линейка может.

Строительство с помощью только линейки или только компаса

Возможно (согласно Теорема Мора – Маскерони ), чтобы построить что-либо с помощью только компаса, если это можно построить с помощью линейки и компаса, при условии, что данные и данные, которые необходимо найти, состоят из дискретных точек (не линий или кругов). Истинность этой теоремы зависит от истинности аксиомы Архимеда,^[15] что не является первопорядком по своей природе.

Невозможно извлечь квадратный корень с помощью одной линейки, поэтому некоторые вещи, которые нельзя построить с помощью линейки, можно построить с помощью циркуля; но (по Теорема Понселе – Штейнера ) по единственному кругу и его центру их можно построить.

Расширенные конструкции

Древние греки классифицировали конструкции на три основные категории в зависимости от сложности инструментов, необходимых для их решения. Если в конструкции использовались только линейка и циркуль, ее называли планарной; если также требовалось одно или несколько конических сечений (кроме круга), то его называли сплошным; в третью категорию вошли все конструкции, не попавшие ни в одну из двух других категорий.^[16] Эта категоризация хорошо сочетается с современной алгебраической точкой зрения. Комплексное число, которое может быть выражено только с помощью полевых операций и квадратных корней (как описано над ) имеет плоскую конструкцию. Комплексное число, включающее также извлечение кубических корней, имеет прочную конструкцию.

На языке полей плоское комплексное число имеет степень двойки и лежит в расширение поля это можно разбить на башню полей, где каждое расширение имеет степень два. Комплексное число, имеющее прочную конструкцию, имеет степень с простыми множителями только два и три и лежит в расширении поля, которое находится на вершине башни полей, где каждое расширение имеет степень 2 или 3.

Прочные конструкции

Точка имеет прочную конструкцию, если ее можно построить с помощью линейки, циркуля и (возможно, гипотетического) инструмента для рисования конусов, который может рисовать любую конусу с уже построенным фокусом, направляющей и эксцентриситетом. Такой же набор точек часто можно построить с помощью меньшего набора инструментов. Например, используя циркуль, линейку и лист бумаги, на котором у нас есть парабола y = x² вместе с точками (0,0) и (1,0) можно построить любое комплексное число, имеющее прочную конструкцию. Точно так же инструмент, который может нарисовать любой эллипс с уже построенными фокусами и большой осью (подумайте, две булавки и кусок веревки), столь же эффективен.^[17]

Древние греки знали, что удвоение куба и деление на три части произвольного угла имеют твердые конструкции. Архимед дал прочную конструкцию правильного 7-угольника. Квадратура круга не имеет твердой конструкции.

Обычный п-gon имеет прочную конструкцию тогда и только тогда, когда п=2^j3^kм куда м является продуктом различных Простые числа Пьерпона (простые числа вида 2^р3^s+1). Набор таких п это последовательность

7, 9, 13, 14, 18, 19, 21, 26, 27, 28, 35, 36, 37, 38, 39, 42, 45, 52, 54, 56, 57, 63, 65, 70, 72, 73, 74, 76, 78, 81, 84, 90, 91, 95, 97 ... (последовательность A051913 в OEIS )

Набор п для которых постоянный п-угольник не имеет твердой конструкции - это последовательность

11, 22, 23, 25, 29, 31, 33, 41, 43, 44, 46, 47, 49, 50, 53, 55, 58, 59, 61, 62, 66, 67, 69, 71, 75, 77, 79, 82, 83, 86, 87, 88, 89, 92, 93, 94, 98, 99, 100... (последовательность A048136 в OEIS )

Как и в случае с простыми числами Ферма, остается открытым вопрос, существует ли бесконечное количество простых чисел Пьерпонта.

Трисекция угла

Что, если бы вместе с линейкой и циркулем у нас был инструмент, который мог бы (только) разрезать пополам произвольный угол? Такие конструкции являются прочными конструкциями, но существуют номера с прочными конструкциями, которые нельзя построить с помощью такого инструмента. Например, мы не можем удвоить куб с помощью такого инструмента.^[18] С другой стороны, любой правильный n-угольник, имеющий твердую конструкцию, можно построить с помощью такого инструмента.

Оригами

В математическая теория оригами более мощный, чем линейка и конструкция компаса. Складки, удовлетворяющие аксиомам Хузиты – Хатори, могут построить точно такой же набор точек, что и расширенные конструкции, с помощью циркуля и инструмента для рисования конусов. Следовательно, оригами также может использоваться для решения кубических уравнений (и, следовательно, уравнений четвертой степени) и, таким образом, решения двух классических задач.^[19]

Яркие правители

Архимед, Никомед и Аполлоний дал конструкции с использованием размеченной линейки. Это позволило бы им, например, взять отрезок, две линии (или окружности) и точку; а затем нарисуйте линию, проходящую через заданную точку и пересекающую три прямые, и такую, чтобы расстояние между точками пересечения равнялось заданному отрезку. Это греки называли Neusis («наклон», «тенденция» или «грани»), потому что новая строка имеет тенденцию В этой расширенной схеме мы можем разрезать пополам произвольный угол (см. Трисечение архимеда ) или извлеките произвольный кубический корень (благодаря Никомеду). Следовательно, любое расстояние, отношение которого к существующему расстоянию является решением кубический или уравнение четвертой степени конструктивно. Используя размеченную линейку, правильные многоугольники с твердыми конструкциями, например семиугольник, являются конструктивными; и Джон Х. Конвей и Ричард К. Гай дать конструкции для нескольких из них.^[20]

Конструкция neusis более мощная, чем инструмент конического рисования, так как можно построить комплексные числа, не имеющие твердых конструкций. Фактически, с помощью этого инструмента можно решить некоторые квинтики, которые не решается радикалами.^[21] Известно, что нельзя решить неприводимый многочлен простой степени, большей или равной 7, с помощью конструкции Neusis, поэтому с помощью этого инструмента невозможно построить правильный 23-угольник или 29-угольник. Бенджамин и Снайдер доказали, что можно построить правильный 11-угольник, но не дали конструкции.^[22] Пока не ясно, можно ли построить с помощью этого инструмента обычный 25-угольник или 31-угольник.

Вычисление двоичных цифр

В 1998 г. Саймон Плафф дал линейку и компас алгоритм что можно использовать для вычисления двоичные цифры определенных номеров.^[23]Алгоритм включает многократное удвоение угла и становится физически непрактичным после примерно 20 двоичных цифр.

Смотрите также

• Карлайл круг
• Геометрическая криптография
• Геометрография
• Список программного обеспечения для интерактивной геометрии, на большинстве из них изображены линейка и компас.
• Математика складывания бумаги
• Андервуд Дадли, математик, который занимался сбором ложных проверок с помощью линейки и компаса.

Рекомендации

внешняя ссылка

• Правильные многоугольные конструкции доктора Математики в Математический форум @ Drexel
• Строительство только с помощью компаса в завязать узел
• Трисекция угла по Гиппократу в завязать узел
• Вайсштейн, Эрик В. "Угловая тройка". MathWorld.