Тетрактагон - Tetracontagon

Обычный тетраконтагон
Обычный тетраконтагон
Тип	Правильный многоугольник
Края и вершины	40
Символ Шлефли	{40}, т {20}, тт {10}, ттт {5}
Диаграмма Кокстера
Группа симметрии	Двугранный (D40), заказ 2 × 40
Внутренний угол (градусы )	171°
Двойной многоугольник	Себя
Характеристики	Выпуклый, циклический, равносторонний, изогональный, изотоксальный

В геометрия, а тетраконтагон или тессараконтагон это сорокугольник многоугольник или 40-гон.^[1][2] Сумма внутренних углов любого тетраконтагона составляет 6840 градусов.

Обычный тетраконтагон

А обычный тетраконтагон представлен Символ Шлефли {40} а также может быть выполнен в виде усеченный икосагон, t {20}, который чередует два типа ребер. Кроме того, он также может быть сконструирован как дважды усеченный десятиугольник, tt {10}, или трижды усеченный пятиугольник, ttt {5}.

Один внутренний угол в правильном четырехугольнике равен 171 °, что означает, что один внешний угол будет равен 9 °.

В площадь правильного тетраконтагона (с т = длина кромки)

${ displaystyle { begin {align} A = 10t ^ {2} cot { frac { pi} {40}} = & 10 left (1 + { sqrt {5}} + { sqrt {5+) 2 { sqrt {5}}}} + { sqrt { left (1 + { sqrt {5}} + { sqrt {5 + 2 { sqrt {5}}}} right) ^ {2 } +1}} right) t ^ {2} = & 10 left (1 + { sqrt {5}} + { sqrt {5 + 2 { sqrt {5}}}} + { sqrt { left (1 + { sqrt {5}} right) ^ {2} + { binom {2} {1}} left (1 + { sqrt {5}} right) { sqrt { 5 + 2 { sqrt {5}}}} + left ({ sqrt {5 + 2 { sqrt {5}}}} right) ^ {2} +1}} right) t ^ {2 } = & 10 left (1 + { sqrt {5}} + { sqrt {5 + 2 { sqrt {5}}}} + { sqrt { left (6 + { binom {2}) {1}} { sqrt {5}} right) ^ {} + { binom {2} {1}} left (1 + { sqrt {5}} right) { sqrt {5 + 2 { sqrt {5}}}} + left (5 + 2 { sqrt {5}} right) ^ {} + 1}} right) t ^ {2} = & 10 left (1+ { sqrt {5}} + { sqrt {5 + 2 { sqrt {5}}}} + { sqrt { left (11 + 4 { sqrt {5}} + { binom {2} { 1}} left (1 + { sqrt {5}} right) { sqrt {5 + 2 { sqrt {5}}}} right) +1}} right) t ^ {2} = & 10 left (1 + { sqrt {5}} + { sqrt {5 + 2 { sqrt {5}}}} + { sqrt {12 + 4 { sqrt {5}} + { binom {2} {1}} left (1 + { sqrt {5}} right) { sqrt {5 + 2 { sqrt {5}}}}}} right) t ^ {2} конец {выровнен}}}$

и это inradius является

${ displaystyle r = { frac {1} {2}} t cot { frac { pi} {40}}}$

Фактор ${ displaystyle cot { frac { pi} {40}}}$ является корнем октическое уравнение ${ displaystyle x ^ {8} -8x ^ {7} -60x ^ {6} -8x ^ {5} + 134x ^ {4} + 8x ^ {3} -60x ^ {2} + 8x + 1}$.

В по окружности правильного тетраконтагона

${ displaystyle { begin {align} R = { frac {1} {2}} t csc { frac { pi} {40}} end {align}}}$

Поскольку 40 = 2³ × 5 правильный четырехугольник конструктивный с помощью компас и линейка.^[3] Как усеченный икосагон, его можно построить с помощью ребраделение пополам обычного икосагона. Это означает, что значения ${ displaystyle sin { frac { pi} {40}}}$ и ${ displaystyle cos { frac { pi} {40}}}$ может быть выражено в радикалах следующим образом:

${ displaystyle sin { frac { pi} {40}} = { frac {1} {4}} ({ sqrt {2}} - 1) { sqrt {{ frac {1} {2} }} (2 + { sqrt {2}}) (5 + { sqrt {5}})}} - { frac {1} {8}} { sqrt {2 - { sqrt {2}} }} (1 + { sqrt {2}}) ({ sqrt {5}} - 1)}$

${ displaystyle cos { frac { pi} {40}} = { frac {1} {8}} ({ sqrt {2}} - 1) { sqrt {2 + { sqrt {2} }}} ({ sqrt {5}} - 1) + { frac {1} {4}} (1 + { sqrt {2}}) { sqrt {{ frac {1} {2}} (2 - { sqrt {2}}) (5 + { sqrt {5}})}}}$

Построение правильного четырехугольника

Правильный четырехугольник с данной описанной окружностью

Дана окружность

1. Постройте сначала длину стороны JE₁ из пятиугольник.
2. Перенесите это на описанную окружность, возникнет пересечение E₃₉.
3. Подключите точку E₃₉ с центральной точкой M возникает угол E₃₉МЕНЯ₁ с 72 °.
4. Уменьшить угол E вдвое₃₉МЕНЯ₁, возникает пересечение E₄₀ а угол E₄₀МЕНЯ₁ с 9 °.
5. Подключите точку E₁ с точкой E₄₀, возникает длина первой стороны а тетраконтагона.
6. Наконец, вы переносите сегмент E₁E₄₀ (длина стороны а) несколько раз против часовой стрелки по описанной окружности, пока не появится правильный четырехугольник.

Золотое сечение

${ displaystyle { frac { overline {JM}} { overline {BJ}}} = { frac { overline {BM}} { overline {JM}}} = { frac {1 + { sqrt {5}}} {2}} = varphi приблизительно 1,618}$

Длина стороны указана

Правильный четырехугольник с заданной длиной стороны
(Конструкция очень похожа на икосагон с заданной длиной стороны )

1. Нарисуйте сегмент E₄₀E₁ длина которого указана длина стороны а тетраконтагона.
2. Расширить сегмент E₄₀E₁ более чем в два раза.
3. Нарисуйте каждую дугу окружности вокруг точек E₁ и E₄₀, возникают пересечения A и B.
4. Проведите вертикальную прямую линию от точки B до точки A.
5. Нарисуйте параллельную линию и отрезок AB из точки E₁ с дугой окружности возникает пересечение D.
6. Нарисуйте дугу окружности вокруг точки C с радиусом компакт диск пока к продолжению длины стороны не возникает пересечение F.
7. Нарисуйте дугу окружности вокруг точки E₄₀ с радиусом E₄₀F до вертикальной прямой возникает пересечение G и угол E₄₀GE₁ с 36 °.
8. Нарисуйте дугу окружности вокруг точки G с радиусом E₄₀г до вертикальной прямой возникает пересечение H и угол E₄₀ОН₁ с 18 °.
9. Нарисуйте дугу окружности вокруг точки H с радиусом E₄₀ЧАС до вертикальной прямой возникает центральная точка M описанной окружности и угол E₄₀МЕНЯ₁ с 9 °.
10. Проведите вокруг центральной точки M радиусом E₄₀M описанная окружность четырехугольника.
11. Наконец перенесите сегмент E₄₀E₁ (длина стороны а) несколько раз против часовой стрелки по описанной окружности до тех пор, пока не появится правильный четырехугольник.

Золотое сечение

${ displaystyle { frac { overline {E_ {40} E_ {1}}} { overline {E_ {1} F}}} = { frac { overline {E_ {40} F}} { overline {E_ {40} E_ {1}}}} = { frac {1 + { sqrt {5}}} {2}} = varphi приблизительно 1,618}$

Симметрия

Симметрии правильного четырехугольника. Голубыми линиями показаны подгруппы индекса 2. Левый и правый подграфы позиционно связаны подгруппами индекса 5.

В обычный тетраконтагон есть Dih₄₀ двугранная симметрия, порядок 80, представленный 40 линиями отражения. Dih₄₀ имеет 7 диэдральных подгрупп: (Dih₂₀, Ди₁₀, Ди₅) и (Dih₈, Ди₄, Ди₂, Ди₁). Также есть еще восемь циклический симметрии как подгруппы: (Z₄₀, Z₂₀, Z₁₀, Z₅) и (Z₈, Z₄, Z₂, Z₁), причем Z_п представляющий π /п радианная вращательная симметрия.

Джон Конвей обозначает эти более низкие симметрии буквой, а порядок симметрии следует за буквой.^[4] Он дает d (диагональ) с зеркальными линиями через вершины, п с зеркальными линиями по краям (перпендикулярно), я с зеркальными линиями через вершины и края, и грамм для вращательной симметрии. а1 этикетки не симметричны.

Эти более низкие симметрии позволяют степеням свободы определять неправильные четырехугольники. Только g40 подгруппа не имеет степеней свободы, но может рассматриваться как направленные края.

Рассечение

40-угольник с 560 ромбами

обычный

Изотоксал

Coxeter заявляет, что каждый зоногон (а 2м-угольник, противоположные стороны которого параллельны и равной длины) можно разрезать на м(м-1) / 2 параллелограмма. Эти мозаики содержатся в виде подмножеств вершин, ребер и граней в ортогональных проекциях. м-кубики^[5]В частности, это верно для правильных многоугольников с равным числом сторон, и в этом случае все параллелограммы являются ромбическими. Для обычный тетраконтагон, м= 20, и его можно разделить на 190: 10 квадратов и 9 наборов по 20 ромбов. Это разложение основано на Многоугольник Петри проекция 20-куб.

Примеры

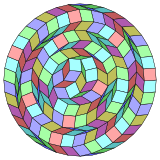Тетрактаграмма

Тетрактаграмма - это 40-гранная звездный многоугольник. Есть семь обычных форм, которые дает Символы Шлефли {40/3}, {40/7}, {40/9}, {40/11}, {40/13}, {40/17} и {40/19}, и 12 соединений звездные фигуры с тем же конфигурация вершины.

Обычный звездные многоугольники {40 / к}

Рисунок	{40/3}	{40/7}	{40/9}	{40/11}	{40/13}	{40/17}	{40/19}
Внутренний угол	153°	117°	99°	81°	63°	27°	9°

Правильные составные многоугольники

Рисунок	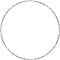{40/2}=2{20}	{40/4}=4{10}	{40/5}=5{8}	{40/6}=2{20/3}	{40/8}=8{5}	{40/10}=10{4}
Внутренний угол	162°	144°	135°	126°	108°	90°
Рисунок	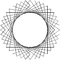{40/12}=4{10/3}	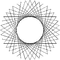{40/14}=2{20/7}	{40/15}=5{8/3}	{40/16}=8{5/2}	{40/18}=2{20/9}	{40/20}=20{2}
Внутренний угол	72°	54°	45°	36°	18°	0°

Много изогональный тетрактаграммы также могут быть построены как более глубокие усечения регулярных икосагон {20} и икосаграммы {20/3}, {20/7} и {20/9}. Они также создают четыре квазиусечения: t {20/11} = {40/11}, t {20/13} = {40/13}, t {20/17} = {40/17} и t {20 / 19} = {40/19}. Некоторые изогональные тетраконтаграммы изображены ниже в виде усеченной последовательности с конечными точками t {20} = {40} и t {20/19} = {40/19}.^[6]

t {20} = {40}
				т {20/19} = {40/19}

Рекомендации

внешняя ссылка

• Вайсштейн, Эрик В. «Тетраконтагон». MathWorld.
• Именование многоугольников и многогранников
• тессараконтагон