Изогональная фигура - Википедия - Isogonal figure
В геометрия, а многогранник (а многоугольник, многогранник или мозаика, например) изогональный или же вершинно-транзитивный если все это вершины эквивалентны относительно симметрии фигуры. Это означает, что каждая вершина окружена одними и теми же типами лицо в том же или обратном порядке и с одинаковыми углами между соответствующими гранями.
Технически мы говорим, что для любых двух вершин существует симметрия многогранника, отображающего первый изометрически на второй. Другие способы сказать это: группа автоморфизмов многогранника действует переходно на его вершинах, или что вершины лежат в пределах одного орбита симметрии.
Все вершины конечного п-мерная изогональная фигура существует на (п−1) -сфера.[нужна цитата ]
Период, термин изогональный давно используется для многогранников. Вершинно-транзитивный синоним, заимствованный из современных идей, таких как группы симметрии и теория графов.
В псевдоромбокубооктаэдр - который нет изогональный - демонстрирует, что простое утверждение, что «все вершины выглядят одинаково», не так ограничительно, как используемое здесь определение, которое включает группу изометрий, сохраняющую многогранник или мозаику.
Изогональные многоугольники и апейрогоны
| Изогональный апейрогоны |
|---|
 |
| Изогональный косые апейрогоны |
Все правильные многоугольники, апейрогоны и правильные звездчатые многоугольники находятся изогональный. В двойной изогонального многоугольника является изотоксальный многоугольник.
Некоторые чётные полигоны и апейрогоны которые чередуют две длины кромки, например прямоугольник, находятся изогональный.
Все плоские изогональные 2п-угольники имеют двугранная симметрия (Dп, п = 2, 3, ...) с линиями отражения через средние точки края.
| D2 | D3 | D4 | D7 |
|---|---|---|---|
 Изогональный прямоугольники и скрещенные прямоугольники разделяя то же самое расположение вершин | 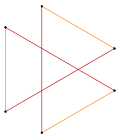 Изогональный гексаграмма с 6 одинаковыми вершинами и 2 длинами ребер.[1] | 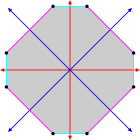 Изогонально выпуклый восьмиугольник с синими и красными радиальными линиями отражения | 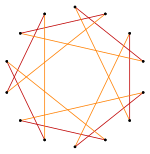 Изогональная «звезда» четырехугольник с одним типом вершины и двумя типами ребер[2] |
Изогональные многогранники и 2D мозаики
 |
| Искаженный квадратная черепица |
 |
| Искаженный усеченная квадратная мозаика |
An изогональный многогранник а 2D-мозаика имеет единственный вид вершины. An изогональный многогранник со всеми правильными гранями также равномерный многогранник и может быть представлен конфигурация вершины обозначение, упорядочивающее грани вокруг каждой вершины. Геометрически искаженные вариации однородных многогранников и мозаик также могут иметь конфигурацию вершин.
| D3D, заказ 12 | Тчас, заказ 24 | Очас, заказ 48 | |
|---|---|---|---|
| 4.4.6 | 3.4.4.4 | 4.6.8 | 3.8.8 |
 Искаженный шестиугольная призма (дитригональная трапеция) |  Искаженный ромбокубооктаэдр | 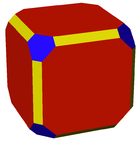 Мелкий усеченный кубооктаэдр |  Гиперусеченный куб |
Изогональные многогранники и двумерные мозаики можно дополнительно классифицировать:
- Обычный если это также равногранный (лицо-переходное) и изотоксальный (реберно-транзитивный); это означает, что каждое лицо - это один и тот же правильный многоугольник.
- Квазирегулярный если это также изотоксальный (реберно-транзитивный), но не равногранный (лицо-переходное).
- Полурегулярный если каждая грань представляет собой правильный многоугольник, но это не равногранный (лицо-переходный) или изотоксальный (реберно-транзитивный). (Определение различается у разных авторов; например, некоторые исключают тела с двугранной симметрией или невыпуклые тела.)
- Униформа если каждая грань является правильным многоугольником, т. е. правильным, квазирегулярным или полурегулярным.
- Полуформ если его элементы также изогональны.
- Чешуйчатый если все края одинаковой длины.
- благородный если это также равногранный (лицо-переходное).
N размеры: изогональные многогранники и мозаики
Эти определения могут быть расширены до многомерных многогранники и мозаика. Все однородные многогранники находятся изогональный, например, равномерные 4-многогранники и выпуклые однородные соты.
В двойной изогонального многогранника является равногранная фигура, который транзитивен на своем грани.
k-изогональные и k-унифицированные фигуры
Многогранник или мозаику можно назвать k-изогональный если его вершины образуют k классы транзитивности. Более ограничительный срок, k-униформа определяется как k-изогональная фигура построен только из правильные многоугольники. Визуально они могут быть представлены цветами разными равномерные раскраски.
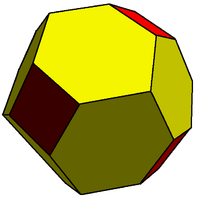 Этот усеченный ромбический додекаэдр является 2-изогональный потому что он содержит два класса транзитивности вершин. Этот многогранник состоит из квадраты и сплющенный шестиугольники. |  Этот полурегулярная черепица это также 2-изогональный (и 2-униформа). Эта плитка сделана из равносторонний треугольник и регулярный шестиугольник лица. |  2-изогональный 9/4 эннеаграмма (лицо окончательная звездчатость икосаэдра ) |
Смотрите также
- Edge-транзитивный (Изотоксический показатель)
- Лицо-переходный (Изогранная фигура)
Рекомендации
- ^ Кокстер, Плотности правильных многогранников II, стр. 54-55, фигура вершины «гексаграммы» h {5 / 2,5}.
- ^ Светлая сторона математики: материалы конференции Мемориала Эжена Стренса по развлекательной математике и ее истории, (1994), Метаморфозы полигонов, Бранко Грюнбаум, Рисунок 1. Параметр т=2.0
- Питер Р. Кромвель, Многогранники, Издательство Кембриджского университета 1997, ISBN 0-521-55432-2, п. 369 Транзитивность
- Грюнбаум, Бранко; Шепард, Г.С. (1987). Плитки и узоры. В. Х. Фриман и компания. ISBN 0-7167-1193-1. (стр.33 k-изогональный черепица, стр. 65 k-однородные мозаики)
внешняя ссылка
- Вайсштейн, Эрик В. «Вершинно-транзитивный граф». MathWorld.
- Ольшевский, Георгий. «Транзитивность». Глоссарий по гиперпространству. Архивировано из оригинал 4 февраля 2007 г.
- Ольшевский, Георгий. «Изогонал». Глоссарий по гиперпространству. Архивировано из оригинал 4 февраля 2007 г.
- Изогональные калейдоскопические многогранники Владимир Львович Булатов, Физический факультет, Университет штата Орегон, Корваллис, представленный на Mosaic2000, Millennium Open Symposium on the Arts and Interdisciplinary Computing, 21–24 августа 2000 г., Сиэтл, Вашингтон. Модели VRML
- Стивен Датч использует термин k-uniform для перечисления k-изогональных мозаик.
- Список n-однородных мозаик
- Вайсштейн, Эрик В. "Демирегулярная мозаика". MathWorld. (Также используется термин k-uniform для k-isogonal)
