Ромб - Rhombus
| Ромб | |
|---|---|
 Два ромба | |
| Тип | четырехугольник, параллелограмм, воздушный змей |
| Края и вершины | 4 |
| Символ Шлефли | { } + { } {2α} |
| Диаграмма Кокстера | |
| Группа симметрии | Двугранный (D2), [2], (* 22), порядок 4 |
| Площадь | (половина произведения диагоналей) |
| Двойной многоугольник | прямоугольник |
| Характеристики | выпуклый, изотоксальный |

В самолете Евклидова геометрия, а ромб (множественное число ромбовидные или ромбы) это четырехугольник все четыре стороны которого имеют одинаковую длину. Другое имя равносторонний четырехугольник, поскольку равносторонний означает, что все его стороны равны по длине. Ромб часто называют алмаз, после бриллианты костюм в игральные карты что напоминает проекцию восьмигранный алмаз, или лепешка, хотя первое иногда относится конкретно к ромбу с углом 60 ° (который некоторые авторы называют Калиссон после французское сладкое[1] - также см Полиалмаз ), а под последним иногда понимают именно ромб с углом 45 °.
Каждый ромб просто (несамопересекающиеся), и является частным случаем параллелограмм и воздушный змей. Ромб с прямыми углами - это квадрат.[2][3]
Этимология
Слово «ромб» происходит от Греческий ῥόμβος (ромбы), что означает то, что вращается,[4] которое происходит от глагола ῥέμβω (rhembō), что означает «вертеться кругом».[5] Слово использовалось как Евклид и Архимед, который употребил термин «сплошной ромб» для обозначения биконус, два правых циркуляра шишки разделяя общую базу.[6]
Поверхность, которую мы называем ромб сегодня поперечное сечение биконуса на плоскости через вершины двух конусов.
Характеристики
А просто (несамопересекающийся ) четырехугольник - ромб если и только если это любое из следующих:[7][8]
- а параллелограмм в котором диагональ делит пополам внутренний угол
- параллелограмм, у которого не менее двух последовательных сторон равны по длине
- параллелограмм, в котором диагонали перпендикулярны ( ортодиагональный параллелограмм)
- четырехугольник с четырьмя сторонами одинаковой длины (по определению)
- четырехугольник, в котором диагонали перпендикуляр и делить пополам друг друга
- четырехугольник, в котором каждая диагональ делит пополам два противоположных внутренних угла
- четырехугольник ABCD имея точку п в своей плоскости так, что четыре треугольника ABP, BCP, CDP, и DAP все конгруэнтный[9]
- четырехугольник ABCD в которой в кругах в треугольниках ABC, BCD, CDA и DAB иметь общую точку зрения[10]
Основные свойства
В каждом ромбе по два диагонали соединяющие пары противоположных вершин и две пары параллельных сторон. С помощью конгруэнтный треугольники, можно доказывать что ромб симметричный по каждой из этих диагоналей. Отсюда следует, что любой ромб обладает следующими свойствами:
- Напротив углы ромба имеют равную меру.
- Две диагонали ромба равны перпендикуляр; то есть ромб - это ортодиагональный четырехугольник.
- Его диагонали делят пополам противоположные углы.
Первое свойство означает, что каждый ромб является параллелограмм. Следовательно, ромб имеет все свойства параллелограмма: например, противоположные стороны параллельны; смежные углы дополнительный; две диагонали делить пополам друг друга; любая линия, проходящая через середину, делит область пополам; а сумма квадратов сторон равна сумме квадратов диагоналей ( закон параллелограмма ). Таким образом, обозначая общую сторону как а и диагонали как п и q, в каждом ромбе
Не каждый параллелограмм является ромбом, хотя любой параллелограмм с перпендикулярными диагоналями (второе свойство) является ромбом. В общем, любой четырехугольник с перпендикулярными диагоналями, одна из которых является линией симметрии, является воздушный змей. Каждый ромб - это воздушный змей, а любой четырехугольник, который одновременно является воздушным змеем и параллелограммом, является ромбом.
Ромб - это тангенциальный четырехугольник.[11] То есть имеет вписанный круг это касается всех четырех сторон.

Диагонали
Длина диагоналей p = AC и q = BD можно выразить через сторону ромба а и один угол при вершине α так как
и
Эти формулы являются прямым следствием закон косинусов.
Inradius
Inradius (радиус круга вписанный в ромбе), обозначенный р, можно выразить через диагонали п и q так как[11]
или по длине стороны а и любой угол при вершине α или β так как
Площадь
Что касается всех параллелограммов, площадь K ромба - произведение его основания и высоты (час). База просто любая длина стороны а:
Площадь также можно выразить как квадрат основания, умноженный на синус любого угла:
или по высоте и углу при вершине:
или как половину произведения диагоналей п, q:
или как полупериметр умножить на радиус круга вписанный в ромбе (inradius):
Другой способ, аналогичный параллелограммам, - рассматривать две смежные стороны как векторы, образующие бивектор, поэтому площадь - это величина бивектора (величина векторного произведения двух векторов), которая является детерминант декартовых координат двух векторов: K = Икс1у2 – Икс2у1.[12]
Двойные свойства
В двойной многоугольник ромба это прямоугольник:[13]
- У ромба все стороны равны, а у прямоугольника все углы равны.
- У ромба противоположные углы равны, а у прямоугольника равны противоположные стороны.
- В ромб вписан круг, а в прямоугольник - описанный круг.
- Ромб имеет ось симметрии через каждую пару противоположных углов при вершине, а прямоугольник имеет ось симметрии через каждую пару противоположных сторон.
- Диагонали ромба пересекаются под равными углами, а диагонали прямоугольника равны по длине.
- Фигура, образованная соединением середин сторон ромба, представляет собой прямоугольник, и наоборот.
Декартово уравнение
Стороны ромба с центром в начале координат и диагоналями, приходящимися на ось, состоят из всех точек (х, у) удовлетворение
Вершины находятся в и Это частный случай суперэллипс, с показателем 1.
Другие свойства
- Один из пяти 2D решетка типов - это ромбическая решетка, также называемая центрированная прямоугольная решетка.
- Идентичные ромбики могут мозаику двухмерной плоскости тремя различными способами, включая, для ромба 60 °, ромбовидная плитка.
| Как топологический квадратные мозаики | Как 30-60 градусов ромбик черепица | |
|---|---|---|
 |  |  |
- Трехмерные аналоги ромба включают бипирамида и биконус.
- Несколько многогранники имеют ромбические грани, такие как ромбический додекаэдр и трапеции-ромбический додекаэдр.
| Изоэдральные многогранники | Неизоэдральные многогранники | |||
|---|---|---|---|---|
| Идентичные ромбы | Идентичные золотые ромбы | Два вида ромбов | Три вида ромбов | |
 | 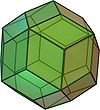 | 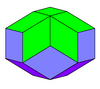 |  |  |
| Ромбический додекаэдр | Ромбический триаконтаэдр | Ромбический икосаэдр | Ромбический эннеконтаэдр | Ромбоэдр |
Как грани многогранника
А ромбоэдр (также называемый ромбическим шестигранником) представляет собой трехмерную фигуру, похожую на кубовид (также называемый прямоугольным параллелепипедом), за исключением того, что его 3 пары параллельных граней представляют собой до трех типов ромбов вместо прямоугольников.
В ромбический додекаэдр это выпуклый многогранник с 12 конгруэнтный ромбы как его лица.
В ромбический триаконтаэдр это выпуклый многогранник с 30 золотые ромбики (ромбы, диагонали которых Золотое сечение ) как его лица.
В большой ромбический триаконтаэдр невыпуклый равногранный, изотоксальный многогранник с 30 пересекающимися ромбическими гранями.
В ромбический гексеконтаэдр это звездчатость ромбического триаконтаэдра. Он невыпуклый с 60 золотой ромбический сталкивается с икосаэдрическая симметрия.
В ромбический эннеконтаэдр представляет собой многогранник, состоящий из 90 ромбических граней, с тремя, пятью или шестью ромбами, пересекающимися в каждой вершине. В нем 60 широких ромбов и 30 тонких.
В трапеции-ромбический додекаэдр - выпуклый многогранник с 6 ромбическими и 6 трапециевидный лица.
В ромбический икосаэдр представляет собой многогранник, состоящий из 20 ромбических граней, три, четыре или пять из которых пересекаются в каждой вершине. У него 10 граней на полярной оси и 10 граней, следующих за экватором.
Смотрите также
- Меркель-Рауте
- Ромб Михаэлиса, в анатомии человека
- Ромбовидный, либо параллелепипед, либо параллелограмм, который не является ни ромбом, ни прямоугольником
- Ромбическая антенна
- Ромбические шахматы
- Флаг департамента Северный Сантандер Колумбии, содержащий четыре звезды в форме ромба
- Суперэллипс (включает ромб со скругленными углами)
Рекомендации
- ^ http://books.google.com/books?id=2F_0DwAAQBAJ&pg=PA28
- ^ Заметка: Евклид Оригинальное определение ромба и определение некоторых английских словарей исключают квадраты, но современные математики предпочитают всеобъемлющее определение.
- ^ Вайсштейн, Эрик В. "Квадрат". MathWorld. инклюзивное использование
- ^ ῥόμβος В архиве 2013-11-08 в Wayback Machine, Генри Джордж Лидделл, Роберт Скотт, Греко-английский лексикон, на Персее
- ^ ρέμβω В архиве 2013-11-08 в Wayback Machine, Генри Джордж Лидделл, Роберт Скотт, Греко-английский лексикон, на Персее
- ^ «Происхождение ромба». Архивировано из оригинал на 2015-04-02. Получено 2005-01-25.
- ^ Залман Усискин и Дженнифер Гриффин "Классификация четырехугольников. Исследование определения В архиве 2020-02-26 в Wayback Machine ", Издательство" Век информации ", 2008 г., стр. 55-56.
- ^ Оуэн Байер, Феликс Лазебник и Дейдре Смелцер, Методы евклидовой геометрии В архиве 2019-09-01 в Wayback Machine, Математическая ассоциация Америки, 2010, стр. 53.
- ^ Пэрис Памфилос (2016), «Характеристика ромба», Форум Geometricorum 16, стр. 331–336, [1] В архиве 2016-10-23 на Wayback Machine
- ^ "IMOmath", 26-я Бразильская математическая олимпиада 2004 г."" (PDF). В архиве (PDF) из оригинала от 18.10.2016. Получено 2020-01-06.
- ^ а б Вайсштейн, Эрик В. "Ромб". MathWorld.
- ^ WildLinAlg, эпизод 4 В архиве 2017-02-05 в Wayback Machine, Норман Дж. Вильдбергер, Univ. Нового Южного Уэльса, 2010 г., лекция на YouTube
- ^ де Вильерс, Майкл, "Равносторонние циклические и равносторонние описанные многоугольники", Математический вестник 95, март 2011 г., 102-107.
внешняя ссылка
- Параллелограмм и ромб - Анимированный курс (Построение, Окружность, Площадь)
- Определение ромба, Открытый справочник по математике с интерактивным апплетом.
- Площадь ромба, Открытый справочник по математике - показывает три различных способа вычисления площади ромба с помощью интерактивного апплета














