Ромбоэдр - Rhombohedron

Ромбоэдр

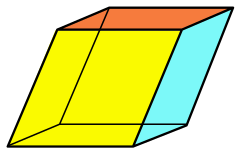Тип	призма
Лица	6 ромбовидные
Края	12
Вершины	8
Группа симметрии	C_я , [2⁺,2⁺], (×), порядок 2
Характеристики	выпуклый, зоноэдр

В геометрия, а ромбоэдр (также называемый ромбический шестигранник) представляет собой трехмерную фигуру, подобную кубовид (также называемый прямоугольным параллелепипедом), за исключением того, что его грани не прямоугольники, а ромбовидные. Это частный случай параллелепипед где все ребра одинаковой длины. Его можно использовать для определения ромбоэдрическая решетчатая система, а соты с ромбоэдрическими ячейками.

В целом ромбоэдр может иметь до трех типов ромбических граней в конгруэнтных противоположных парах, C_я симметрия порядок 2.

Четыре точки, образующие несмежные вершины ромбоэдра, обязательно образуют четыре вершины ромбоэдра. ортоцентрический тетраэдр, и таким образом могут быть образованы все ортоцентрические тетраэдры.^[1]

Ромбоэдрическая решетчатая система

В ромбоэдрическая решетчатая система имеет ромбоэдрические ячейки с 3 парами уникальных ромбических граней:

Особые случаи по симметрии

Частные случаи ромбоэдра

Форма	Куб	Тригональный трапецоэдр	Правильно ромбическая призма	Косая ромбическая призма
Угол ограничения	α = β = γ = 90 °	α = β = γ	α = β = 90 °	α = β
Симметрия	О_час заказ 48	D_3D заказ 12	D_2ч заказ 8	C_2ч заказ 4
Лица	6 квадратов	6 одинаковых ромбов	2 ромба, 4 квадрата	6 ромбов

Куб: с О_час симметрия, порядок 48. Все грани квадраты.
Тригональный трапецоэдр (также называемый равногранный ромбоэдр,^[2] или же ромбический шестигранник^[3]): с D_3D симметрия, порядок 12. Все не тупые внутренние углы граней равны (все грани равны конгруэнтным ромбам). Это можно увидеть, растянув куб по диагональной оси тела. Например, обычный октаэдр с двумя обычными тетраэдры крепится на противоположных сторонах, образует 60-градусный треугольный трапецоэдр.
Правильно ромбическая призма: с D_2ч симметрия, порядок 8. Она построена из двух ромбов и четырех квадратов. Это можно увидеть, растянув куб на его грань диагональной оси. Например, два правых призмы с правильными треугольными основаниями, соединенными вместе, составляет 60 градусов правая ромбическая призма.
Косая ромбическая призма: с C_2ч симметрия, порядок 4. Он имеет только одну плоскость симметрии через четыре вершины и шесть ромбических граней.

Твердая геометрия

Для единицы (т.е. с длиной стороны 1) равногранный ромбоэдр,^[2] с ромбическим острым углом ${ displaystyle theta ~}$ , с одной вершиной в начале координат (0, 0, 0) и с одним ребром, лежащим вдоль оси x, три порождающих вектора

е₁ :

{ Displaystyle { biggl (} 1,0,0 { biggr)},}

е₂ :

{ Displaystyle { biggl (} соз тета, грех тета, 0 { biggr)},}

е₃ :

{ displaystyle { biggl (} cos theta, { cos theta - cos ^ {2} theta over sin theta}, {{ sqrt {1-3 cos ^ {2} theta +2 cos ^ {3} theta}} over sin theta} { biggr)}.}

Остальные координаты можно получить сложением векторов^[4] из 3-х векторов направления: е₁ + е₂ , е₁ + е₃ , е₂ + е₃ , и е₁ + е₂ + е₃ .

Громкость ${ displaystyle V}$ равногранного ромбоэдра по длине стороны ${ displaystyle a}$ и его ромбический острый угол ${ displaystyle theta ~}$ , является упрощением объема параллелепипед, и задается

{ displaystyle V = a ^ {3} (1- cos theta) { sqrt {1 + 2 cos theta}} = a ^ {3} { sqrt {(1- cos theta) ^ {2} (1 + 2 cos theta)}} = a ^ {3} { sqrt {1-3 cos ^ {2} theta +2 cos ^ {3} theta}} ~.}

Мы можем выразить объем ${ displaystyle V}$ по-другому :

{ displaystyle V = 2 { sqrt {3}} ~ a ^ {3} sin ^ {2} left ({ frac { theta} {2}} right) { sqrt {1 - { frac {4} {3}} sin ^ {2} left ({ frac { theta} {2}} right)}} ~.}

Поскольку площадь (ромбической) основы определяется выражением ${ Displaystyle а ^ {2} грех тета ~}$ , а поскольку высота ромбоэдра определяется его объемом, деленным на площадь его основания, высота ${ displaystyle h}$ равногранного ромбоэдра по длине стороны ${ displaystyle a}$ и его ромбический острый угол ${ displaystyle theta}$ дан кем-то

{ displaystyle h = a ~ {(1- cos theta) { sqrt {1 + 2 cos theta}} over sin theta} = a ~ {{ sqrt {1-3 cos ^ {2} theta +2 cos ^ {3} theta}} over sin theta} ~.}

Примечание:

{ Displaystyle ч = а ~ я}

₃ , куда

{ displaystyle z}

₃ третья координата е₃ .

Диагональ тела между остроугольными вершинами самая длинная. Из-за симметрии вращения относительно этой диагонали все остальные три диагонали тела между тремя парами противоположных тупоугольных вершин имеют одинаковую длину.

Смотрите также

Списки фигур

внешняя ссылка

[1] Суд, Н.А. (Октябрь 1934 г.), "Заметки об ортоцентрическом тетраэдре", Американский математический ежемесячный журнал: 499–502, Дои:10.2307/2300415, JSTOR 2300415.

[:0-2] а ^б Линии, Л. (1965). Твердая геометрия: с разделами о пространственных решетках, сферах-пакетах и кристаллах.. Dover Publications.

[3] ttp://www.origamiheaven.com/rhombicpolyhedra.htm

[4] «Сложение векторов». Вольфрам. 17 мая 2016. Получено 17 мая 2016.

[1]

[2]

[3]

[4]