Каталонский твердый - Catalan solid

В математика, а Каталонский твердый, или же Архимедова двойственная, это двойственный многогранник для Архимедово твердое тело. Всего 13 каталонских твердых тел. Они названы в честь бельгийский математик, Эжен Каталонский, который впервые описал их в 1865 году.
Все каталонские твердые тела выпуклые. Они есть лицо переходный но нет вершинно-транзитивный. Это связано с тем, что двойственные архимедовы тела транзитивны по вершинам и не транзитивны по граням. Обратите внимание, что в отличие от Платоновы тела и Архимедовы тела, грани каталонских тел равны нет правильные многоугольники. Тем не менее фигуры вершин твердых веществ Каталонии регулярны, и они имеют постоянный двугранные углы. Каталонские твердые тела являются транзитивными. изоэдра.
Кроме того, два каталонских твердых вещества являются ребро-транзитивный: the ромбический додекаэдр и ромбический триаконтаэдр. Эти двойники из двух квазирегулярный Архимедовы тела.
Как только призмы и антипризмы обычно не считаются архимедовыми телами, поэтому бипирамиды и трапецоэдры обычно не считаются каталонскими твердыми телами, несмотря на то, что они являются переходными по поверхности.
Два каталонских твердых вещества хиральный: the пятиугольный икоситетраэдр и пятиугольный гексеконтаэдр, двойственная киральной курносый куб и курносый додекаэдр. Каждый из них состоит из двух энантиоморфы. Не считая энантиоморфов, бипирамид и трапецоэдров, всего существует 13 каталонских твердых тел.
Симметрия
Каталонские твердые тела вместе с их двойными Архимедовы тела, могут быть сгруппированы в те, которые имеют тетраэдрическую, октаэдрическую и икосаэдрическую симметрию. Как для октаэдрической, так и для икосаэдрической симметрии существует шесть форм. Единственное каталонское твердое тело с подлинной тетраэдрической симметрией - это триакис тетраэдр (двойной усеченный тетраэдр ). Ромбический додекаэдр и тетракис шестигранник имеют октаэдрическую симметрию, но их можно раскрасить, чтобы они имели только тетраэдрическую симметрию. Исправление и курносый также существуют с тетраэдрической симметрией, но они Платонический вместо Архимеда, поэтому их двойники платонические, а не каталонские. (Они показаны на коричневом фоне в таблице ниже.)
| Архимедов (Платонический) |  |  |  |  |  |  |
|---|---|---|---|---|---|---|
| Каталонский (Платонический) |  |  |  |  |  |  |
| Архимедов |  |  |  |  |  |  |
|---|---|---|---|---|---|---|
| Каталонский |  |  |  |  |  |  |
| Архимедов |  |  |  |  |  |  |
|---|---|---|---|---|---|---|
| Каталонский |  |  |  |  |  |  |
Список
| Имя (Двойное имя) Имя Конвей | Картинки | Ортогональный каркасы | Лицо многоугольник | Углы лица (°) | Двугранный угол (°) | Лица | Края | Vert | Сим. |
|---|---|---|---|---|---|---|---|---|---|
| триакис тетраэдр (усеченный тетраэдр ) «кТ» |   |    | Равнобедренный V3.6.6 | 112.885 33.557 33.557 | 129.521 | 12 | 18 | 8 | Тd |
| ромбический додекаэдр (кубооктаэдр ) "jC" |   |    | Ромб V3.4.3.4 | 70.529 109.471 70.529 109.471 | 120 | 12 | 24 | 14 | Очас |
| триакис октаэдр (усеченный куб ) «КО» |   |   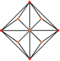 | Равнобедренный V3.8.8 | 117.201 31.400 31.400 | 147.350 | 24 | 36 | 14 | Очас |
| тетракис шестигранник (усеченный октаэдр ) "kC" | 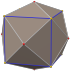  |    | Равнобедренный V4.6.6 | 83.621 48.190 48.190 | 143.130 | 24 | 36 | 14 | Очас |
| дельтовидный икоситетраэдр (ромбокубооктаэдр ) "oC" |   |  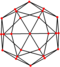  | летающий змей V3.4.4.4 | 81.579 81.579 81.579 115.263 | 138.118 | 24 | 48 | 26 | Очас |
| disdyakis додекаэдр (усеченный кубооктаэдр ) «mC» |   |    | Неравносторонний V4.6.8 | 87.202 55.025 37.773 | 155.082 | 48 | 72 | 26 | Очас |
| пятиугольный икоситетраэдр (курносый куб ) "gC" |   |    | Пентагон V3.3.3.3.4 | 114.812 114.812 114.812 114.812 80.752 | 136.309 | 24 | 60 | 38 | О |
| ромбический триаконтаэдр (икосододекаэдр ) "jD" |   |    | Ромб V3.5.3.5 | 63.435 116.565 63.435 116.565 | 144 | 30 | 60 | 32 | ячас |
| триакис икосаэдр (усеченный додекаэдр ) "ки" |   |    | Равнобедренный V3.10.10 | 119.039 30.480 30.480 | 160.613 | 60 | 90 | 32 | ячас |
| пентакид додекаэдр (усеченный икосаэдр ) "кД" |   |    | Равнобедренный V5.6.6 | 68.619 55.691 55.691 | 156.719 | 60 | 90 | 32 | ячас |
| дельтовидный гексеконтаэдр (ромбикосододекаэдр ) "oD" |   |    | летающий змей V3.4.5.4 | 86.974 67.783 86.974 118.269 | 154.121 | 60 | 120 | 62 | ячас |
| дисьякис триаконтаэдр (усеченный икосододекаэдр ) "мД" |   |    | Неравносторонний V4.6.10 | 88.992 58.238 32.770 | 164.888 | 120 | 180 | 62 | ячас |
| пятиугольный гексеконтаэдр (курносый додекаэдр ) "gD" |   |    | Пентагон V3.3.3.3.5 | 118.137 118.137 118.137 118.137 67.454 | 153.179 | 60 | 150 | 92 | я |
Геометрия
Все двугранные углы каталонского твердого тела равны. Обозначая их стоимость , обозначая угол грани в вершинах, где лица встречаются , у нас есть
- .
Это можно использовать для вычисления и , , ... , из , ... Только.
Треугольные грани
Из 13 каталонских тел 7 имеют треугольные грани. Они имеют вид Vp.q.r, где p, q и r принимают свои значения из 3, 4, 5, 6, 8 и 10. Углы , и можно вычислить следующим образом. Положить , , и положи
- .
потом
- ,
- .
За и выражения, конечно, похожи. В двугранный угол можно вычислить из
- .
Применяя это, например, к дисьякис триаконтаэдр (, и , следовательно , и , куда это Золотое сечение ) дает и .
Четырехугольные грани
Из 13 каталонских тел 4 имеют четырехугольные грани. Они имеют вид Vp.q.p.r, где p, q и r принимают свои значения среди 3, 4 и 5. Угол можно вычислить по следующей формуле:
- .
Из этого, , а двугранный угол легко вычислить. В качестве альтернативы положите , , . потом и можно найти, применив формулы для треугольного случая. Угол конечно, можно вычислить аналогично. воздушные змеи, или если , ромбовидные. Применяя это, например, к дельтовидный икоситетраэдр (, и ), мы получили .
Пятиугольные грани
Из 13 каталонских тел 2 имеют пятиугольные грани. Они имеют вид Vp.p.p.p.q, где p = 3 и q = 4 или 5. Угол можно вычислить, решив уравнение третьей степени:
- .
Метрические свойства
Для каталонского солидного позволять быть двойственным по отношению к средняя сфера из . потом архимедово твердое тело с той же средней сферой. Обозначим длину краев к . Позволять быть inradius лиц , средний радиус и , радиус , и окружной радиус . Тогда эти величины можно выразить через и двугранный угол следующее:
- ,
- ,
- ,
- .
Эти количества связаны соотношением , и .
В качестве примера пусть быть кубооктаэдром с длиной ребра . потом представляет собой ромбический додекаэдр. Применяя формулу для четырехугольных граней с и дает , следовательно , , , .
Все вершины типа лежать на сфере радиуса данный
- ,
и аналогично для .
По сути, есть сфера, которая касается всех граней которые являются регулярными -угольники (и аналогично для ) в их центре. Радиус этой сферы задается
- .
Эти два радиуса связаны соотношением . Продолжая приведенный выше пример: и , который дает , , и .
Если является вершиной типа , край начинается с , и точка, где край касается середины сферы , обозначим расстояние к . Тогда края соединение вершин типа и введите иметь длину . Эти количества могут быть вычислены с помощью
- ,
и аналогично для . Продолжая приведенный выше пример: , , , , поэтому ребра ромбического додекаэдра имеют длину .
Двугранные углы между -гональные и -кональные грани удовлетворить
- .
Завершая пример ромбического додекаэдра, двугранный угол кубооктаэдра определяется выражением .
Применение к другим твердым телам
Все формулы этого раздела применимы к Платоновы тела, и бипирамиды и трапецоэдры с равными двугранными углами также, потому что они могут быть получены только из свойства постоянного двугранного угла. Для пятиугольный трапецоэдр, например, с гранями V3.3.5.3, получаем , или же . Это неудивительно: можно отрезать обе вершины таким образом, чтобы получить правильный додекаэдр.
Смотрите также
- Список однородных мозаик Показывает двойные однородные многоугольные мозаики, похожие на каталонские тела.
- Обозначения многогранника Конвея Процесс построения обозначений
- Архимедово твердое тело
- Джонсон солид
Рекомендации
- Эжен Каталонский Mémoire sur la Théorie des Polyèdres. J. l'École Polytechnique (Париж) 41, 1-71, 1865.
- Алан Холден Формы, пространство и симметрия. Нью-Йорк: Довер, 1991.
- Веннингер, Магнус (1983), Двойные модели, Издательство Кембриджского университета, ISBN 978-0-521-54325-5, МИСТЕР 0730208 (Тринадцать полуправильных выпуклых многогранников и их двойники)
- Уильямс, Роберт (1979). Геометрическая основа естественной структуры: первоисточник дизайна. Dover Publications, Inc. ISBN 0-486-23729-X. (Раздел 3-9)
- Энтони Пью (1976). Многогранники: визуальный подход. Калифорния: Калифорнийский университет Press в Беркли. ISBN 0-520-03056-7. Глава 4: Двойники архимедовых многогранников, призмы и антипризмы
внешняя ссылка
- Вайсштейн, Эрик В. "Каталонские твердые вещества". MathWorld.
- Вайсштейн, Эрик В. "Изогедр". MathWorld.
- Каталонские твердые вещества - в визуальных многогранниках
- Архимедовы двойники - в Многогранниках виртуальной реальности
- Интерактивный каталонский солид в Java
- Ссылка для скачивания оригинальной публикации Каталонии за 1865 год - с красивыми рисунками, формат PDF