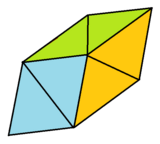
Тригональный трапецоэдр - Trigonal trapezohedron
| Тригональный трапецоэдр | |
|---|---|
 | |
| Тип | трапецоэдр |
| Обозначение Конвея | dA3 |
| Диаграмма Кокстера | |
| Лица | 6 ромбовидные |
| Края | 12 |
| Вершины | 8 |
| Конфигурация лица | 3,3,3,3 |
| Группа симметрии | D3D, [2+, 6], (2 * 3), порядок 12 |
| Группа вращения | D3, [2,3]+, (223), порядок 6 |
| Двойной многогранник | тригональный антипризма |
| Характеристики | выпуклый, лицо переходный |
В геометрия, а тригональный трапецоэдр, или же треугольный дельтоэдр[1], или же равногранный ромбоэдр[2], или же ромбический шестигранник[3] представляет собой трехмерную фигуру, образованную шестью конгруэнтный ромбовидные.
Шесть одинаковых ромбических граней могут составить две конфигурации тригональных трапеций. В острый или же вытянутый форма имеет три острых угловых угла ромбических граней, пересекающихся в вершинах двух полярных осей. В тупой или же сплюснутый или же плоский форма имеет три тупоугольных угла ромбических граней, пересекающихся в вершинах двух полярных осей.
А треугольный трапецоэдр является равногранный ромбоэдр. (Генерал ромбоэдр допускает до трех типов ромбических граней, трех разных ромбических углов, с порядком симметрии 2.)
Геометрия
Тригональные трапецоэдры - особый вид параллелепипеды, и являются единственными параллелепипедами с шестью конгруэнтными гранями. Поскольку все ребра должны иметь одинаковую длину, каждый тригональный трапецоэдр также является ромбоэдр.
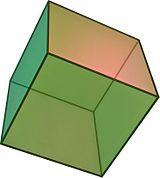 Треугольный трапецоэдр с квадрат лица это куб. |  А ромбический додекаэдр можно разрезать на 4 одинаковых тупых тригональных трапецоэдра. |  В ромбический гексеконтаэдр можно разделить на 20 острые золотые ромбоэдры встреча в центральной точке. |
Золотой ромбоэдр
 Острая форма |  Тупая форма |
В золотые ромбоэдры два частных случая треугольный трапецоэдр с золотой ромб лица. В острый или же вытянутый форма имеет три острых угловых угла ромбических граней, пересекающихся в вершинах двух полярных осей. В тупой или же сплюснутый или же плоский форма имеет три тупоугольных угла ромбических граней, пересекающихся в вершинах двух полярных осей.
Связанные многогранники
Асимметричная вариация
Вариация более низкой симметрии треугольный трапецоэдр имеет только вращательную симметрию, D3, и состоит из 6 одинаковых нерегулярных четырехугольники.[4] У этих четырехугольников обязательно есть две смежные стороны равной длины. Эта форма представляет собой витой трапецииэдр за п=3.
| Полярная ось | Сторона | Сеть |
|---|---|---|
 |  |  |
Обычный октаэдр дополненный на 2 обычных тетраэдры создает треугольный трапецоэдр, с компланарной равносторонние треугольники сливаются в ромбические грани под углом 60 градусов.
Это простейший из трапецоэдров, бесконечная последовательность многогранники которые двойной к антипризмы. В двойной из треугольный трапецоэдр это треугольная антипризма.
| Семья п-гональный трапецоэдры | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Изображение многогранника |  |  |  |  |  |  |  |  | ... | Апейрогональный трапецоэдр | |
| Сферическое мозаичное изображение |  |  |  |  |  |  |  |  | Плоское мозаичное изображение | ||
| Конфигурация лица Vп.3.3.3 | V2.3.3.3 | V3.3.3.3 | V4.3.3.3 | V5.3.3.3 | V6.3.3.3 | V7.3.3.3 | V8.3.3.3 | V10.3.3.3 | V12.3.3.3 | ... | V∞.3.3.3 |
Смотрите также
Рекомендации
- ^ http://mathworld.wolfram.com/TrigonalTrapezohedron.html
- ^ Линии, Л. (1965). Твердая геометрия: с разделами о пространственных решетках, сферах-пакетах и кристаллах.. Dover Publications.
- ^ http://www.origamiheaven.com/rhombicpolyhedra.htm
- ^ Fair Dice: Тригональный трапецоэдр с асимметричными сторонами
| Этот многогранник -связанная статья является заглушка. Вы можете помочь Википедии расширяя это. |