Закон косинусов - Law of cosines

Рис. 1 - Треугольник. Углы α (или же А), β (или же B), и γ (или же C) соответственно противоположны сторонам а, б, и c.

Тригонометрия
Контур История использование Функции  (обратный ) Обобщенная тригонометрия
Ссылка
Идентичности Точные константы Столы Единичный круг
Законы и теоремы
Синусы Косинусы Касательные Котангенсы теорема Пифагора
Исчисление
Тригонометрическая замена Интегралы  (обратные функции ) Производные

В тригонометрия, то закон косинусов (также известный как формула косинуса, правило косинуса, или же аль-Каши теорема^[1]) связывает длины сторон треугольник к косинус одного из углы. Используя обозначения, как на рис.1, закон косинусов утверждает

${displaystyle c ^ {2} = a ^ {2} + b ^ {2} -2abcos gamma,}$

куда γ обозначает угол между сторонами отрезков а и б и противоположная сторона длины c. Для того же рисунка два других соотношения аналогичны:

${displaystyle a ^ {2} = b ^ {2} + c ^ {2} -2bccos alpha,}$

${displaystyle b ^ {2} = a ^ {2} + c ^ {2} -2accos eta.}$

Закон косинусов обобщает теорема Пифагора, что справедливо только для прямоугольные треугольники: если угол γ - прямой угол (меры 90 градусы, или же π/2 радианы ), тогда потому что γ = 0, а значит, закон косинусов уменьшает к теорема Пифагора:

${displaystyle c ^ {2} = a ^ {2} + b ^ {2}.}$

Закон косинусов полезен для вычисления третьей стороны треугольника, когда известны две стороны и их внутренний угол, и для вычисления углов треугольника, если известны все три стороны.

История

Рис.2 - Тупой треугольник ABC с перпендикулярным BH

Хотя понятие косинус еще не был разработан в его время, Евклид с Элементы, относящаяся к III веку до нашей эры, содержит раннюю геометрическую теорему, почти эквивалентную закону косинусов. Случаи тупые треугольники и острые треугольники (соответствующие двум случаям отрицательного или положительного косинуса) рассматриваются отдельно в предложениях 12 и 13 Книги 2. Поскольку тригонометрические функции и алгебра (в частности, отрицательные числа) отсутствуют во времена Евклида, утверждение имеет более геометрический оттенок:

Предложение 12.
В треугольниках с тупым углом квадрат на стороне, образующей тупой угол, больше квадратов на сторонах, содержащих тупой угол, в два раза больше прямоугольника, содержащегося на одной из сторон относительно тупого угла, а именно того, на который падает перпендикуляр, и прямая, отрезанная снаружи перпендикуляром к тупому углу.

— Евклида Элементы, перевод Томас Л. Хит.^[2]

Используя обозначения, как на рис.2, утверждение Евклида можно представить формулой

${displaystyle AB ^ {2} = CA ^ {2} + CB ^ {2} +2 (CA) (CH).}$

Эту формулу можно преобразовать в закон косинусов, отметив, что CH = (CB) cos (π - γ) = −(CB) cos γ. Предложение 13 содержит полностью аналогичное утверждение для острых треугольников.

Евклида Элементы проложил путь к открытию закона косинусов. В 15 веке Джамшид аль-Каши, персидский математик и астроном, представил первое явное изложение закона косинусов в форме, подходящей для триангуляция. Он предоставил точные тригонометрические таблицы и выразил теорему в форме, пригодной для современного использования. По состоянию на 1990-е годы в Франция, закон косинусов по-прежнему называется Теорема д'Аль-Каши.^[1][3][4]

Теорема была популяризирована в западный мир к Франсуа Виет в 16 веке. В начале XIX века современные алгебраические обозначения позволили записать закон косинусов в его нынешней символической форме.

Приложения

Рис. 3 - Применение закона косинусов: неизвестная сторона и неизвестный угол.

Теорема используется в триангуляция, чтобы решить треугольник или круг, т.е. найти (см. рисунок 3):

• третья сторона треугольника, если известны две стороны и угол между ними:

${displaystyle, c = {sqrt {a ^ {2} + b ^ {2} -2abcos gamma}} ,;}$

• углы треугольника, если известны три стороны:

${displaystyle, gamma = arccos left ({frac {a ^ {2} + b ^ {2} -c ^ {2}} {2ab}} ight) ,;}$

• третья сторона треугольника, если известны две стороны и угол, противоположный одной из них (можно также использовать теорема Пифагора сделать это, если это прямоугольный треугольник ):

${displaystyle, a = bcos gamma pm {sqrt {c ^ {2} -b ^ {2} sin ^ {2} gamma}} ,.}$

Эти формулы производят высокие ошибки округления в плавающая точка вычисления, если треугольник очень острый, т.е. если c мала по сравнению с а и б или же γ мала по сравнению с 1. Можно даже получить результат немного больше единицы для косинуса угла.

Третья показанная формула является результатом решения для а в квадратное уровненеие а² − 2ab потому что γ + б² − c² = 0. Это уравнение может иметь 2, 1 или 0 положительных решений, соответствующих количеству возможных треугольников с учетом данных. У него будет два положительных решения, если б грех γ < c < б, только одно положительное решение, если c = б грех γ, и нет решения, если c < б грех γ. Эти разные случаи также объясняются неоднозначность конгруэнтности бокового угла.

Доказательства

Используя формулу расстояния

Рис.4 - Доказательство координатной геометрии

Рассмотрим треугольник со сторонами длины а, б, c, куда θ измерение угла, противоположного стороне длины c. Этот треугольник можно разместить на Декартова система координат по краю а с началом в C, построив компоненты трех точек треугольника, как показано на рисунке 4:

${displaystyle A = (bcos heta, bsin heta), B = (a, 0), {ext {and}} C = (0,0).}$

Посредством формула расстояния,

${displaystyle c = {sqrt {(a-bcos heta) ^ {2} + (0-bsin heta) ^ {2}}}.}$

Квадрат с обеих сторон и упрощение

${displaystyle {egin {выровнено} c ^ {2} & {} = (a-bcos heta) ^ {2} + (- bsin heta) ^ {2} c ^ {2} & {} = a ^ {2 } -2abcos heta + b ^ {2} cos ^ {2} heta + b ^ {2} sin ^ {2} heta c ^ {2} & {} = a ^ {2} + b ^ {2} ( sin ^ {2} heta + cos ^ {2} heta) -2abcos heta c ^ {2} & {} = a ^ {2} + b ^ {2} -2abcos heta .end {выровнено}}}$

Преимущество этого доказательства состоит в том, что оно не требует рассмотрения разных случаев, когда треугольник острый, прямой или тупой.

Использование тригонометрии

Рис.5 - Острый треугольник с перпендикуляром

Отбрасывая перпендикуляр на стороне c через точку C, высота треугольника, показывает (см. рис. 5)

${displaystyle c = acos eta + bcos alpha.}$

(Это все еще верно, если α или же β тупой, и в этом случае перпендикуляр выходит за пределы треугольника.) Умножение на c дает

${displaystyle c ^ {2} = accos eta + bccos alpha.}$

Рассмотрение двух других высот треугольника дает

${displaystyle a ^ {2} = accos eta + abcos gamma,}$

${displaystyle b ^ {2} = bccos alpha + abcos gamma.}$

Добавление двух последних уравнений дает

${displaystyle a ^ {2} + b ^ {2} = accos eta + bccos alpha + 2abcos gamma.}$

Вычитание первого уравнения из последнего приводит к

${displaystyle a ^ {2} + b ^ {2} -c ^ {2} = accos eta + bccos alpha + 2abcos gamma - (accos eta + bccos alpha)}$

что упрощает

${displaystyle c ^ {2} = a ^ {2} + b ^ {2} -2abcos gamma.}$

Это доказательство использует тригонометрия в том, что он рассматривает косинусы различных углов как самостоятельные величины. Он использует тот факт, что косинус угла выражает отношение между двумя сторонами, охватывающими этот угол в любой прямоугольный треугольник. Другие доказательства (ниже) являются более геометрическими, поскольку они рассматривают такие выражения, как а потому что γ просто как метка для длины определенного отрезка линии.

Многие доказательства относятся к случаям тупых и острых углов. γ раздельно.

Использование теоремы Пифагора

Тупой треугольник ABC с высотой BH

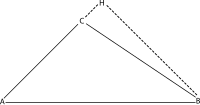
Случай тупого угла

Евклид доказал эту теорему, применив теорема Пифагора к каждому из двух прямоугольных треугольников на показанном рисунке (AHB и CHB). С помощью d для обозначения отрезка CH и час на высоту BH, треугольник AHB дает нам

${displaystyle c ^ {2} = (b + d) ^ {2} + h ^ {2},}$

и треугольник CHB дает

${displaystyle d ^ {2} + h ^ {2} = a ^ {2}.}$

Расширение первое уравнение дает

${displaystyle c ^ {2} = b ^ {2} + 2bd + d ^ {2} + h ^ {2}.}$

Подставляя в это второе уравнение, можно получить следующее:

${displaystyle c ^ {2} = a ^ {2} + b ^ {2} + 2bd.}$

Это предложение Евклида 12 из книги 2 Элементы.^[5] Чтобы преобразовать его в современную форму закона косинусов, обратите внимание, что

${displaystyle d = acos (pi -gamma) = - acos gamma.}$

Случай острого угла

Доказательство Евклидом его предложения 13 происходит по той же схеме, что и его доказательство предложения 12: он применяет теорему Пифагора к обоим прямоугольным треугольникам, образованным путем опускания перпендикуляра на одну из сторон, образующих угол γ и использует биномиальную теорему для упрощения.

Рис.6 - Краткое доказательство с использованием тригонометрии для случая острого угла

Еще одно доказательство в остром случае

Используя больше тригонометрии, закон косинусов можно вывести с помощью теоремы Пифагора только один раз. Фактически, используя правый треугольник в левой части рисунка 6, можно показать, что:${displaystyle {egin {align} quad c ^ {2} & = (b-acos gamma) ^ {2} + (asin gamma) ^ {2} & = b ^ {2} -2abcos gamma + a ^ {2 } cos ^ {2} гамма + a ^ {2} sin ^ {2} гамма & = b ^ {2} + a ^ {2} -2abcos gamma, конец {выровнен}}}$

с использованием тригонометрическая идентичность

${displaystyle quad cos ^ {2} gamma + sin ^ {2} gamma = 1.}$

Это доказательство нуждается в небольшой модификации, если б < а cos (γ). В этом случае прямоугольный треугольник, к которому применяется теорема Пифагора, перемещается за пределами треугольник ABC. Единственное влияние, которое это оказывает на расчет, состоит в том, что б − а cos (γ) заменяется на а cos (γ) − б. Поскольку эта величина входит в расчет только через свой квадрат, остальная часть доказательства не изменяется. Однако эта проблема возникает только тогда, когда β тупой, и его можно избежать, отразив треугольник вокруг биссектрисы γ.

Обращаясь к рис.6, стоит отметить, что если угол противоположной стороны а является α тогда:

${displaystyle an alpha = {frac {asin gamma} {b-acos gamma}}.}$

Это полезно для прямого вычисления второго угла, когда заданы две стороны и включенный угол.

Используя теорему Птолемея

Доказательство закона косинусов с использованием теоремы Птолемея

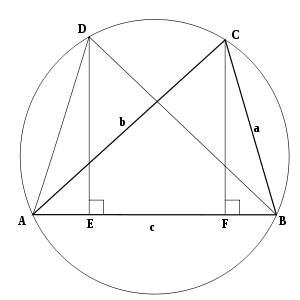
Ссылаясь на схему, треугольник ABC с боков AB = c, до н.э = а и AC = б нарисован внутри описанной окружности, как показано. Треугольник ABD построен конгруэнтно треугольнику ABC с ОБЪЯВЛЕНИЕ = до н.э и BD = AC. Перпендикуляры от D и C встретить базу AB в E и F соответственно. Потом:

${displaystyle {egin {выровнено} & BF = AE = BCcos {hat {B}} = acos {hat {B}} Rightarrow & DC = EF = AB-2BF = c-2acos {hat {B}}. конец {выровнено} }}$

Теперь закон косинусов передается прямым применением Теорема Птолемея к циклический четырехугольник ABCD:

${displaystyle {egin {align} & AD imes BC + AB imes DC = AC imes BD Rightarrow & a ^ {2} + c (c-2acos {hat {B}}) = b ^ {2} Rightarrow & a ^ {2 } + c ^ {2} -2accos {hat {B}} = b ^ {2} .end {выровнено}}}$

Ясно если угол B является верно, тогда ABCD является прямоугольником, и применение теоремы Птолемея дает теорема Пифагора:

${displaystyle a ^ {2} + c ^ {2} = b ^ {2} .quad}$

Сравнивая области

Можно также доказать закон косинусов, вычислив области. Смена знака как угла γ становится тупым, делает необходимым различие падежей.

Напомним, что

• а², б², и c² площади квадратов со сторонами а, б, и c, соответственно;
• если γ остро, то ab потому что γ это площадь параллелограмм с боков а и б образуя угол γ ′ = π/2 − γ;
• если γ тупой, и поэтому потому что γ отрицательно, то −ab потому что γ это площадь параллелограмм с боков а и б образуя угол γ ′ = γ − π/2.

Рис. 7a - Доказательство закона косинусов для острого угла γ путем «вырезания и вставки».

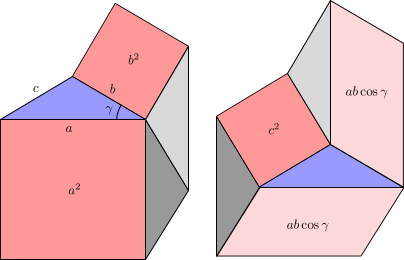
Острый случай. На рис. 7а показан семиугольник разрезать на более мелкие части (двумя разными способами), чтобы получить доказательство закона косинусов. Различные части

• розовым цветом области а², б² слева и области 2ab потому что γ и c² справа;
• синим цветом треугольник ABC, слева и справа;
• серым, вспомогательные треугольники, все конгруэнтный к ABC, равное количество (а именно 2) как слева, так и справа.

Равенство площадей слева и справа дает

${displaystyle, a ^ {2} + b ^ {2} = c ^ {2} + 2abcos gamma,.}$

Рис. 7b - Доказательство закона косинусов для тупого угла γ путем «вырезания и вставки».

Тупой случай. Рисунок 7b разрезает шестиугольник двумя разными способами на более мелкие части, что дает доказательство закона косинусов в случае, когда угол γ тупой. У нас есть

• розовым цветом области а², б², и −2ab потому что γ слева и c² справа;
• синим цветом треугольник ABC дважды, как слева, так и справа.

Равенство площадей слева и справа дает

${displaystyle, a ^ {2} + b ^ {2} -2abcos (gamma) = c ^ {2}.}$

Строгое доказательство должно включать доказательства того, что различные формы конгруэнтный и поэтому имеют равную площадь. Это будет использовать теорию конгруэнтные треугольники.

Использование геометрии круга

С использованием геометрия круга, можно дать больше геометрический доказательство, чем использование теорема Пифагора один. Алгебраический манипуляции (в частности биномиальная теорема ) избегаются.

Рис. 8а - Треугольник ABC (розовый), вспомогательный круг (голубой) и вспомогательный прямоугольный треугольник (желтый)

Случай острого угла γ, куда а > 2б потому что γ. Отбросьте перпендикуляр из А на а = до н.э, создавая отрезок линии длиной б потому что γ. Дублируйте прямоугольный треугольник сформировать равнобедренный треугольник ACP. Построить круг с центром А и радиус б, и это касательная час = BH через B. Касательная час образует прямой угол с радиусом б (Евклидов Элементы: Книга 3, предложение 18; или посмотреть здесь ), поэтому желтый треугольник на рисунке 8 - правый. Применить теорема Пифагора чтобы получить

${displaystyle c ^ {2} = b ^ {2} + h ^ {2}.}$

Затем используйте касательная теорема о секущей (Евклидов Элементы: Книга 3, предложение 36), в котором говорится, что квадрат касательной, проходящей через точку B вне круга равно произведению двух отрезков прямых (от B) созданный любым секущий круга через B. В данном случае: BH² = до н.э·BP, или же

${displaystyle h ^ {2} = a (a-2bcos gamma).}$

Подстановка в предыдущее уравнение дает закон косинусов:

${displaystyle c ^ {2} = b ^ {2} + a (a-2bcos gamma).}$

Обратите внимание, что час² это мощность по делу B относительно круга. Использование теорем Пифагора и теоремы о касательном секансе может быть заменено одним применением теорема о силе точки.

Рис. 8b - Треугольник ABC (розовый), вспомогательный круг (голубой) и два вспомогательных прямоугольных треугольника (желтый)

Случай острого угла γ, куда а < 2б потому что γ. Отбросьте перпендикуляр из А на а = до н.э, создавая отрезок линии длиной б потому что γ. Дублируйте прямоугольный треугольник сформировать равнобедренный треугольник ACP. Построить круг с центром А и радиус б, а аккорд через B перпендикулярно c = AB, половина из которых час = BH. Применить теорема Пифагора чтобы получить

${displaystyle b ^ {2} = c ^ {2} + h ^ {2}.}$

Теперь используйте теорема о хорде (Евклидов Элементы: Книга 3, предложение 35), в котором говорится, что если две хорды пересекаются, произведение двух отрезков, полученных на одном хорде, равно произведению двух отрезков, полученных на другом хорде. В данном случае: BH² = до н.э·BP, или же

${displaystyle h ^ {2} = a (2bcos gamma -a).}$

Подстановка в предыдущее уравнение дает закон косинусов:

${displaystyle b ^ {2} = c ^ {2} + a (2bcos gamma -a) ,.}$

Обратите внимание, что сила точки B относительно круга имеет отрицательное значение −час².

Рис. 9 - Доказательство закона косинусов с использованием теоремы о степени точки.

Случай тупого угла γ. В этом доказательстве напрямую используется сила точечной теоремы, без вспомогательных треугольников, получаемых путем построения касательной или хорды. Постройте круг с центром B и радиус а (см. рисунок 9), который пересекает секущий через А и C в C и K. В мощность по делу А относительно круга равно как AB² − до н.э² и AC·АК. Следовательно,

${displaystyle {egin {выровнен} c ^ {2} -a ^ {2} & {} = b (b + 2acos (pi -gamma)) & {} = b (b-2acos gamma), конец {выровнен} }}$

что является законом косинусов.

Использование алгебраических мер для отрезков прямых (позволяющих отрицательные числа как длины отрезков) случай тупого угла (СК > 0) и острый угол (СК < 0) можно лечить одновременно.

Используя закон синусов

Используя закон синуса и зная, что углы треугольника должны составлять в сумме 180 градусов, мы имеем следующую систему уравнений (три неизвестных - это углы):

${displaystyle {frac {c} {sin gamma}} = {frac {b} {sin eta}},}$

${displaystyle {frac {c} {sin gamma}} = {frac {a} {sin alpha}},}$

${displaystyle alpha + eta + gamma = pi.}$

Тогда, используя третье уравнение системы, мы получим систему из двух уравнений с двумя переменными:

${displaystyle {frac {c} {sin gamma}} = {frac {b} {sin (alpha + gamma)}},}$

${displaystyle {frac {c} {sin gamma}} = {frac {a} {sin alpha}},}$

где мы использовали тригонометрическое свойство, что синус дополнительный угол равен синусу угла.

Используя тождество (см. Сумма углов и тождества разностей )

${displaystyle sin (alpha + gamma) = sin alpha cos gamma + sin gamma cos alpha}$

приводит к

${displaystyle c (sin alpha cos gamma + sin gamma cos alpha) = bsin gamma,}$

${displaystyle csin alpha = asin gamma.}$

Разделив всю систему на потому что γ, у нас есть:

${displaystyle c (sin alpha + an gamma cos alpha) = b an gamma,}$

${displaystyle {frac {csin alpha} {cos gamma}} = a гамма,}$

${displaystyle {frac {c ^ {2} sin ^ {2} alpha} {cos ^ {2} gamma}} = a ^ {2} an ^ {2} gamma.}$

Следовательно, из первого уравнения системы можно получить

${displaystyle {frac {csin alpha} {b-ccos alpha}} = гамма}$

Подставляя это выражение во второе уравнение и используя

${displaystyle 1+ an ^ {2} gamma = {frac {1} {cos ^ {2} gamma}}}$

мы можем получить одно уравнение с одной переменной:

${displaystyle c ^ {2} sin ^ {2} alpha left [1+ {frac {c ^ {2} sin ^ {2} alpha} {(b-ccos alpha) ^ {2}}} ight] = a ^ {2} cdot {frac {c ^ {2} sin ^ {2} alpha} {(b-ccos alpha) ^ {2}}}}$

Умножая на (б − c потому что α)², можно получить следующее уравнение:

${displaystyle (b-ccos alpha) ^ {2} + c ^ {2} sin ^ {2} alpha = a ^ {2}.}$

Из этого следует

${displaystyle b ^ {2} -2bccos alpha + c ^ {2} cos ^ {2} alpha + c ^ {2} sin ^ {2} alpha = a ^ {2}.}$

Напоминая о Пифагорейская идентичность, получаем закон косинусов:

${displaystyle a ^ {2} = b ^ {2} + c ^ {2} -2bccos alpha.}$

Использование векторов

Обозначить

${displaystyle {overrightarrow {CB}} = {vec {a}}, {overrightarrow {CA}} = {vec {b}}, {overrightarrow {AB}} = {vec {c}}}$

Следовательно,

${displaystyle {vec {c}} = {vec {a}} - {vec {b}}}$

Принимая скалярное произведение каждой стороны с собой:

${displaystyle {vec {c}} cdot {vec {c}} = ({vec {a}} - {vec {b}}) cdot ({vec {a}} - {vec {b}})}$

${displaystyle Vert {vec {c}} Vert ^ {2} = Vert {vec {a}} Vert ^ {2} + Vert {vec {b}} Vert ^ {2} -2, {vec {a}} cdot {vec {b}}}$

Используя тождество (см. Скалярное произведение )

${displaystyle {vec {u}} cdot {vec {v}} = Vert {vec {u}} Vert, Vert {vec {v}} Vert cos angle ({vec {u}}, {vec {v}}) }$

приводит к

${displaystyle Vert {vec {c}} Vert ^ {2} = Vert {vec {a}} Vert ^ {2} + {Vert {vec {b}} Vert} ^ {2} -2, Vert {vec {a }} Vert!; Vert {vec {b}} Vert cos angle ({vec {a}}, {vec {b}})}$

Результат следует.

Равнобедренный случай

Когда а = б, т.е. когда треугольник равнобедренный с двумя сторонами, падающими на угол γ равных, закон косинусов значительно упрощается. А именно потому, что а² + б² = 2а² = 2ab, закон косинусов принимает вид

${displaystyle cos gamma = 1- {frac {c ^ {2}} {2a ^ {2}}}}$

или же

${displaystyle c ^ {2} = 2a ^ {2} (1-cos гамма).}$

Аналог для тетраэдров

Аналогичное утверждение начинается с того, что α, β, γ, δ быть площадями четырех граней тетраэдр. Обозначим двугранные углы к ${displaystyle {widehat {eta gamma}}}$ и т.д. Тогда^[6]

${displaystyle alpha ^ {2} = eta ^ {2} + gamma ^ {2} + delta ^ {2} -2left [eta gamma cos left ({widehat {eta gamma}} ight) + gamma delta cos left ({widehat {gamma delta}} ight) + delta eta cos left ({widehat {delta eta}} ight) ight].}$

Версия для малых углов

Когда угол, γ, малая и соседние стороны, а и б, имеют одинаковую длину, правая часть стандартной формы закона косинусов может потерять большую точность числовой потеря значимости. В ситуациях, когда это важно, математически эквивалентная версия закона косинусов, подобная формула гаверсина, может оказаться полезным:

${Displaystyle {начало {выровнено} c ^ {2} & = (ab) ^ {2} + 4absin ^ {2} left ({frac {gamma} {2}} ight) & = (ab) ^ {2} + 4aboperatorname {haversin} (гамма) .end {выровнено}}}$

В пределе бесконечно малого угла закон косинусов вырождается в длина дуги окружности формула c = а γ.

В сферической и гиперболической геометрии

Сферический треугольник решается по закону косинусов.

Версии, аналогичные закону косинусов для евклидовой плоскости, также справедливы для единичной сферы и гиперболической плоскости. В сферическая геометрия, треугольник определяется тремя точками ты, v, и ш на единичной сфере, а дуги большие круги соединяя эти точки. Если эти большие круги образуют углы А, B, и C с противоположных сторон а, б, c затем сферический закон косинусов утверждает, что выполняются оба следующих отношения:

${displaystyle {egin {выровнен} cos a & = cos bcos c + sin bsin ccos A cos A & = - cos Bcos C + sin Bsin Ccos a.end {выровнен}}}$

В гиперболическая геометрия, пара уравнений вместе известна как гиперболический закон косинусов. Первый

${displaystyle cosh a = cosh bcosh c-sinh bsinh ccos A}$

куда грех и шиш являются гиперболический синус и косинус, а второй -

${displaystyle cos A = -cos Bcos C + sin Bsin Ccosh a.}$

Как и в евклидовой геометрии, можно использовать закон косинусов для определения углов А, B, C от знания сторон а, б, c. В отличие от евклидовой геометрии в обеих неевклидовых моделях возможно и обратное: углы А, B, C определить стороны а, б, c.

Единая формула для поверхностей постоянной кривизны

Определение двух функций ${displaystyle cos _ {R}}$ и ${displaystyle sin _ {R}}$ в качестве

${displaystyle cos _ {R} (x) = cos (x / R) quad}$ и ${displaystyle quad sin _ {R} (x) = Rcdot sin (x / R)}$

позволяет унифицировать формулы для самолет, сфера и псевдосфера в:

${displaystyle cos _ {R} (BC) = cos _ {R} (AB) cdot cos _ {R} (AC) + {frac {1} {R ^ {2}}} sin _ {R} (AB) cdot sin _ {R} (AC) cdot cos ({widehat {BAC}}).}$

В этих обозначениях ${displaystyle R}$ это комплексное число, представляющий поверхность радиус кривизны.

• За ${displaystyle Rin mathbb {R}}$ поверхность - это сфера радиуса ${displaystyle R}$, а его постоянная кривизна равна ${displaystyle 1 / R ^ {2};}$

• за ${displaystyle R = iR'colon R'in mathbb {R}}$ поверхность - это псевдосфера (мнимого) радиуса ${displaystyle R,}$ с постоянной кривизной равно ${displaystyle 1 / R ^ {2} = - 1 / R '^ {2};}$

• за ${displaystyle R o infty}$ : поверхность стремится к евклидовой самолет, с постоянной нулевой кривизной.

Проверка формулы неевклидовой геометрии

В первых двух случаях ${displaystyle cos _ {R}}$ и ${displaystyle sin _ {R}}$ четко определены в целом комплексная плоскость для всех ${displaystyle Req 0}$, и получить предыдущие результаты очень просто.

Следовательно, для сферы радиуса ${displaystyle 1}$

${displaystyle cos (BC) = cos (AB) cdot cos (AC) + sin (AB) cdot sin (AC) cdot cos ({widehat {BAC}})}$.

Аналогично, для псевдосферы радиуса ${displaystyle i}$

${displaystyle cosh (BC) = cosh (AB) cdot cosh (AC) -sinh (AB) cdot sinh (AC) cdot cos ({widehat {BAC}}).}$

В самом деле, ${displaystyle cosh (x) = cos (x / i)}$ и ${displaystyle sinh (x) = icdot sin (x / i).}$

Проверка формулы в пределе евклидовой геометрии

В евклидовой плоскости необходимо вычислить соответствующие пределы для приведенного выше уравнения:

${displaystyle cos _ {R} (x) = cos (x / R) = 1- {frac {1} {2}} cdot {frac {x ^ {2}} {R ^ {2}}} + oleft ( {гидроразрыв {1} {R ^ {4}}} ight)}$

и

${displaystyle sin _ {R} (x) = Rcdot sin (x / R) = x + oleft ({frac {1} {R ^ {3}}} ight)}$.

Применяя это к общей формуле для конечного ${displaystyle R}$ дает:

${displaystyle {egin {align} 1- {frac {BC ^ {2}} {2R ^ {2}}} + oleft [{frac {1} {R ^ {4}}} ight] = {} & left [1 - {frac {AB ^ {2}} {2R ^ {2}}} + oleft ({frac {1} {R ^ {4}}} ight) ight] cdot left [1- {frac {AC ^ {2 }} {2R ^ {2}}} + oleft ({frac {1} {R ^ {4}}} ight) ight] + [5pt] & {} + {frac {1} {R ^ {2} }} left [AB + oleft ({frac {1} {R ^ {3}}} ight) ight] cdot left [AC + oleft ({frac {1} {R ^ {3}}} ight) ight] cdot cos ({widehat {BAC}}) конец {выровнено}}}$

Собирая термины, умножая на ${displaystyle -2R ^ {2},}$ и принимая ${displaystyle R o infty}$ дает ожидаемую формулу:

${displaystyle BC ^ {2} = AB ^ {2} + AC ^ {2} -2cdot ABcdot ACcdot cos ({widehat {BAC}}).}$

Смотрите также

• Формула половинной стороны
• Закон синусов
• Закон касательных
• Закон котангенсов
• Список тригонометрических тождеств
• Формула Моллвейде
• Решение треугольников
• Триангуляция

Рекомендации

внешняя ссылка

• "Теорема косинусов", Энциклопедия математики, EMS Press, 2001 [1994]
• Несколько выводов закона косинусов, включая закон Евклида. в завязать узел
• Интерактивный апплет закона косинусов