Комплексная плоскость - Complex plane

В математика, то комплексная плоскость или же z-самолет является геометрическим представлением сложные числа установленный реальная ось и перпендикуляр мнимая ось. Его можно рассматривать как модифицированный Декартова плоскость, с реальная часть комплексного числа, представленного смещением по оси x, и мнимая часть перемещением по оси ординат.[примечание 1]
Концепция комплексной плоскости позволяет геометрическую интерпретацию комплексных чисел. Под добавление, они добавляют лайк векторов. В умножение двух комплексных чисел проще всего выразить через полярные координаты - величина или модуль продукта - продукт двух абсолютные значения, или модули, а угол или же аргумент продукта - это сумма двух углов или аргументов. В частности, умножение на комплексное число по модулю 1 действует как поворот.
Комплексную плоскость иногда называют Самолет Арганд или же Самолет Гаусса.
Условные обозначения
В комплексный анализ, комплексные числа обычно обозначаются символом z, который можно разделить на его реальные (Икс) и мнимой (у) части:
Например: z = 4 + 5я, куда Икс и у настоящие числа, и я это мнимая единица. В этой привычной записи комплексное число z соответствует точке (Икс, у) в Декартова плоскость.
На декартовой плоскости точка (Икс, у) также могут быть представлены в полярные координаты в качестве
В декартовой плоскости можно предположить, что арктангенс принимает значения от -π / 2 к π / 2 (в радианы ), и необходимо позаботиться о том, чтобы определить более полную функцию арктангенса для точек (Икс, у) когда Икс ≤ 0.[заметка 2] В комплексной плоскости эти полярные координаты принимают вид
куда
Здесь |z| это абсолютная величина или же модуль комплексного числа z; θ, то аргумент из z, обычно берется на интервале 0 ≤ θ < 2π; и последнее равенство (к |z|еiθ) взято из Формула Эйлера. Без ограничения диапазона θ, аргумент z многозначен, потому что комплексная экспоненциальная функция периодическая, с периодом 2π я. Таким образом, если θ одно значение arg (z), остальные значения даются arg (z) = θ + 2nπ, куда п - любое целое ≠ 0.[2]
Хотя геометрическое представление комплексных чисел редко используется явно, оно неявно основано на его структура евклидова векторного пространства размерности 2, где внутренний продукт комплексных чисел ш и z дан кем-то ; затем для комплексного числа z его абсолютное значение |z| совпадает со своей евклидовой нормой, а его аргумент аргумент (z) с углом поворота от 1 доz.
Теория контурная интеграция составляет большую часть комплексного анализа. В этом контексте важно направление движения по замкнутой кривой - изменение направления, в котором пересекается кривая, увеличивает значение интеграла на -1. По соглашению положительный направление против часовой стрелки. Например, единичный круг проходит в положительном направлении, когда мы начинаем с точки z = 1, затем пройдите вверх и влево через точку z = я, затем вниз и влево через −1, затем вниз и вправо через -я, и, наконец, вверх и вправо до z = 1, с чего мы начали.
Практически весь комплексный анализ связан с сложные функции - то есть с функциями, которые отображают некоторое подмножество комплексной плоскости в какое-то другое (возможно, перекрывающееся или даже идентичное) подмножество комплексной плоскости. Здесь принято говорить о домен из ж(z) как лежащий в z-самолет, имея в виду ассортимент из ж(z) как набор точек в ш-самолет. В символах пишем
и часто думаю о функции ж как преобразование из z-плоскость (с координатами (Икс, у)) в ш-плоскость (с координатами (ты, v)).
Диаграмма Аргана
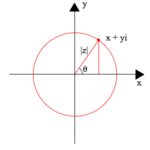
Диаграмма Аргана относится к геометрическому участок комплексных чисел как точки z = x + iy, используя ось x как действительную ось и ось y как мнимую ось.[3] Такие участки названы в честь Жан-Робер Арган (1768–1822), хотя впервые они были описаны норвежско-датским землемером и математиком. Каспар Вессель (1745–1818).[примечание 4] Диаграммы Аргана часто используются для определения положения нули и полюсы функции на комплексной плоскости.
Стереографические проекции

Может быть полезно думать о комплексной плоскости, как если бы она занимала поверхность сферы. Учитывая сфера единичного радиуса, поместите его центр в начало комплексной плоскости, ориентируя так, чтобы экватор на сфере совпадал с единичным кругом в плоскости, а северный полюс находился «над» плоскостью.
Мы можем установить индивидуальная переписка между точками на поверхности сферы за вычетом северного полюса и точками на комплексной плоскости следующим образом. Для данной точки на плоскости проведите прямую линию, соединяющую ее с северным полюсом на сфере. Эта линия будет пересекать поверхность сферы ровно в одной точке. Смысл z = 0 будет проецироваться на южный полюс сферы. Поскольку внутренняя часть единичного круга лежит внутри сферы, вся эта область (|z| < 1) будет нанесен на карту южного полушария. Сама единичная окружность (|z| = 1) будет отображаться на экватор, а внешность единичной окружности (|z| > 1) будет нанесен на карту северного полушария без северного полюса. Ясно, что эта процедура обратима - для любой точки на поверхности сферы, не являющейся северным полюсом, мы можем провести прямую линию, соединяющую эту точку с северным полюсом и пересекающую плоскую плоскость ровно в одной точке.
В рамках этой стереографической проекции северный полюс не связан ни с одной точкой комплексной плоскости. Мы улучшаем взаимно однозначное соответствие, добавляя еще одну точку к комплексной плоскости - так называемую точка в бесконечности - и отождествляя его с северным полюсом на сфере. Это топологическое пространство, комплексная плоскость плюс бесконечно удаленная точка, известно как расширенная комплексная плоскость. При обсуждении комплексного анализа мы говорим об одной «бесконечно удаленной точке». На экране есть две бесконечно удаленные точки (положительная и отрицательная). действительная числовая линия, но есть только одна бесконечно удаленная точка (северный полюс) на расширенной комплексной плоскости.[5]
Представьте на мгновение, что произойдет с линиями широты и долготы, когда они будут проецироваться со сферы на плоскую плоскость. Все линии широты параллельны экватору, поэтому они станут идеальными кругами с центром в начале координат. z = 0. И линии долготы станут прямыми линиями, проходящими через начало координат (а также через «точку в бесконечности», поскольку они проходят как через северный, так и через южный полюса на сфере).
Это не единственная возможная, но правдоподобная стереографическая ситуация проекции сферы на плоскость, состоящую из двух или более значений. Например, северный полюс сферы может быть помещен поверх начала координат. z = −1 в плоскости, касательной к окружности. Детали особого значения не имеют. Любая стереографическая проекция сферы на плоскость создаст одну «точку в бесконечности», и она отобразит линии широты и долготы на сфере в окружности и прямые линии, соответственно, на плоскости.
Режем самолет
При обсуждении функций комплексной переменной часто удобно думать о резать в комплексной плоскости. Эта идея естественно возникает в нескольких различных контекстах.
Многозначные отношения и точки ветвления
Рассмотрим простое двузначное отношение
Прежде чем мы сможем рассматривать эти отношения как однозначные функция, диапазон результирующего значения нужно как-то ограничить. Когда имеешь дело с квадратными корнями из неотрицательных действительных чисел, это легко сделать. Например, мы можем просто определить
быть неотрицательным действительным числом у такой, что у2 = Икс. Эта идея не так хорошо работает в двумерной комплексной плоскости. Чтобы понять почему, давайте подумаем о том, как ценность ж(z) меняется в зависимости от точки z перемещается по единичному кругу. Мы можем написать
Очевидно, как z движется по кругу, ш очерчивает только половину круга. Таким образом, одно непрерывное движение в комплексной плоскости преобразовало положительный квадратный корень е0 = 1 в отрицательный квадратный корень ея = −1.
Эта проблема возникает из-за того, что точка z = 0 имеет только один квадратный корень, а любое другое комплексное число z ≠ 0 имеет ровно два квадратных корня. На прямой числовой линии мы могли бы обойти эту проблему, установив «барьер» в единственной точке. Икс = 0. В комплексной плоскости необходим более крупный барьер, чтобы любой замкнутый контур не мог полностью охватить точка ветвления z = 0. Обычно это делается путем введения срезанная ветка; в этом случае «разрез» может выходить из точки z = 0 вдоль положительной вещественной оси до бесконечно удаленной точки, так что аргумент переменной z в плоскости сечения ограничивается диапазоном 0 ≤ arg (z) < 2π.
Теперь мы можем дать полное описание ш = z½. Для этого нам понадобятся две копии z-плоскость, каждый из них разрезан по реальной оси. На одном экземпляре мы определяем квадратный корень из 1 как e0 = 1, а с другой стороны, мы определяем квадратный корень из 1 как ея = -1. Мы называем эти две копии полной разрезанной плоскости листы. Приводя аргумент непрерывности, мы видим, что (теперь однозначная) функция ш = z½ отображает первый лист в верхнюю половину ш-плоскость, где 0 ≤ arg (ш) < π, сопоставляя второй лист с нижней половиной ш-самолет (где π ≤ arg (ш) < 2π).[6]
Отрезок ветви в этом примере не обязательно должен лежать вдоль действительной оси. Это даже не обязательно должна быть прямая линия. Любая непрерывная кривая, соединяющая начало координат z = 0 с точкой на бесконечности будет работать. В некоторых случаях отрезок ветви даже не должен проходить через бесконечно удаленную точку. Например, рассмотрим отношения
Здесь многочлен z2 - 1 исчезает, когда z = ± 1, поэтому грамм очевидно, имеет две точки ветвления. Мы можем «разрезать» плоскость по действительной оси от -1 до 1 и получить лист, на котором грамм(z) - однозначная функция. Как вариант, разрез может идти от z = 1 вдоль положительной действительной оси через бесконечно удаленную точку, затем продолжить движение «вверх» по отрицательной действительной оси до другой точки ветвления, z = −1.
Эту ситуацию легче всего визуализировать с помощью стереографическая проекция, описанная выше. На сфере один из этих разрезов проходит в продольном направлении через южное полушарие, соединяя точку на экваторе (z = −1) с другой точкой на экваторе (z = 1), и проходя через южный полюс (начало координат, z = 0) в пути. Второй вариант разреза проходит в продольном направлении через северное полушарие и соединяет те же две экваториальные точки, проходя через северный полюс (то есть точку на бесконечности).
Ограничение области определения мероморфных функций
А мероморфная функция сложная функция, которая голоморфный и поэтому аналитический везде в своей области, кроме конечного, или счетно бесконечный, количество баллов.[примечание 5] Точки, в которых такая функция не может быть определена, называются полюса мероморфной функции. Иногда все эти полюса лежат на одной прямой. В этом случае математики могут сказать, что функция «голоморфна на плоскости сечения». Вот простой пример.
В гамма-функция, определяется
куда γ это Константа Эйлера – Маскерони, и имеет простые полюсы в точках 0, −1, −2, −3, ... потому что ровно один знаменатель в бесконечный продукт исчезает, когда z равно нулю или отрицательному целому числу.[примечание 6] Поскольку все его полюса лежат на отрицательной действительной оси, от z = 0 до бесконечно удаленной точки, эта функция может быть описана как «голоморфная на плоскости сечения, разрез проходит вдоль отрицательной действительной оси от 0 (включительно) до бесконечно удаленной точки».
В качестве альтернативы Γ (z) можно было бы описать как «голоморфный в плоскости сечения с -π
Этот крой немного отличается от срезанная ветка мы уже сталкивались, потому что на самом деле исключает отрицательная действительная ось от плоскости сечения. Разрез ветви оставлял действительную ось, соединенную с плоскостью разреза, с одной стороны (0 ≤ θ), но оторвал его от плоскости разреза по другой стороне (θ < 2π).
Конечно, на самом деле нет необходимости исключать весь линейный сегмент из z = 0 до −∞, чтобы построить область, в которой Γ (z) голоморфен. Все, что нам действительно нужно сделать, это прокол плоскость в счетном бесконечном множестве точек {0, −1, −2, −3, ...}. Но замкнутый контур в проколотой плоскости может охватывать один или несколько полюсов Γ (z), давая контурный интеграл который не обязательно равен нулю, по теорема о вычетах. Разрезая комплексную плоскость, мы гарантируем не только то, что Γ (z) голоморфен в этой ограниченной области - мы также гарантируем, что контурный интеграл Γ по любой замкнутой кривой, лежащей в плоскости сечения, тождественно равен нулю.
Определение регионов конвергенции
Многие сложные функции определяются бесконечная серия, или непрерывные дроби. Фундаментальным соображением при анализе этих бесконечно длинных выражений является определение части комплексной плоскости, в которой они сходятся к конечному значению. Как показывают следующие примеры, разрез в плоскости может облегчить этот процесс.
Рассмотрим функцию, определяемую бесконечным рядом
С z2 = (−z)2 для каждого комплексного числа z, ясно что ж(z) является даже функция из z, поэтому анализ можно ограничить половиной комплексной плоскости. А поскольку серия не определена, когда
имеет смысл разрезать плоскость по всей мнимой оси и установить сходимость этого ряда там, где действительная часть z не равняется нулю, прежде чем приступить к более трудной задаче исследования ж(z) когда z это чисто мнимое число.[примечание 7]
В этом примере разрез - простое удобство, потому что точки, в которых бесконечная сумма не определена, изолированы, а резать самолет можно заменить подходящим проколотый самолет. В некоторых случаях резка необходима, а не просто удобна. Рассмотрим бесконечную периодическую цепную дробь
Это можно показать который ж(z) сходится к конечному значению тогда и только тогда, когда z не является отрицательным действительным числом такое, что z <−¼. Другими словами, область сходимости для этой непрерывной дроби является плоскостью сечения, где разрез проходит вдоль отрицательной действительной оси от −¼ до бесконечно удаленной точки.[8]
Склеивание отрезанной плоскости обратно вместе
У нас есть уже видел как отношения
можно преобразовать в однозначную функцию, разделив область определения ж на два несвязанных листа. Также можно «склеить» эти два листа вместе, чтобы сформировать единый Риманова поверхность на котором ж(z) = z1/2 можно определить как голоморфную функцию, образ которой есть весь ш-плоскость (кроме точки ш = 0). Вот как это работает.
Представьте себе две копии комплексной плоскости разреза, причем разрезы проходят вдоль положительной вещественной оси от z = 0 до бесконечности. На одном листе определите 0 ≤ arg (z) < 2π, так что 11/2 = е0 = 1, по определению. На втором листе определите 2π ≤ arg (z) < 4π, так что 11/2 = ея = −1, опять же по определению. Теперь переверните второй лист вверх дном так, чтобы мнимая ось указывала в направлении, противоположном мнимой оси на первом листе, причем обе действительные оси указывали в одном направлении, и «склейте» два листа вместе (так, чтобы край на первый лист с надписью "θ = 0"подключен к краю с меткой"θ < 4π"на втором листе, а край на втором листе помечен"θ = 2π"подключен к краю с меткой"θ < 2π"на первом листе). В результате получается область римановой поверхности, на которой ж(z) = z1/2 однозначно и голоморфно (кроме случаев, когда z = 0).[6]
Чтобы понять почему ж однозначно в этой области, представьте себе контур вокруг единичной окружности, начиная с z = 1 на первом листе. Когда 0 ≤ θ < 2π мы все еще на первом листе. Когда θ = 2π мы перешли на второй лист и вынуждены сделать второй полный обход вокруг точки ветвления z = 0 прежде чем вернуться к нашей отправной точке, где θ = 4π эквивалентно θ = 0, потому что мы склеили два листа вместе. Другими словами, поскольку переменная z делает два полных оборота вокруг точки ветвления, изображение z в ш-плоскость очерчивает только один полный круг.
Формальная дифференциация показывает, что
откуда можно заключить, что производная от ж существует и конечна всюду на римановой поверхности, кроме тех случаев, когда z = 0 (то есть, ж голоморфно, кроме случаев, когда z = 0).
Каким образом риманова поверхность функции
также обсудили над, быть построенным? Еще раз начнем с двух копий z-плоскость, но на этот раз каждый разрезан по реальному отрезку, идущему от z = −1 к z = 1 - это две точки ветвления грамм(z). Мы переворачиваем один из них вверх дном, чтобы две воображаемые оси указывали в противоположных направлениях, и склеиваем соответствующие края двух вырезанных листов. Мы можем проверить, что грамм является однозначной функцией на этой поверхности путем обведения контура вокруг круга единичного радиуса с центром в z = 1. Начиная с точки z = 2 на первом листе мы поворачиваем половину круга до того, как встретимся с разрезом на z = 0. Разрез заставляет нас попасть на второй лист, так что когда z прошел один полный оборот вокруг точки ветвления z = 1, ш прошел всего половину полного оборота, признак ш был отменен (с ея = −1), и наш путь привел нас к точке z = 2 на второй лист поверхности. Пройдя еще пол-оборота, мы встретим другую сторону разреза, где z = 0, и наконец достигаем нашей отправной точки (z = 2 на первый лист) после двух полных оборотов вокруг точки разветвления.
Естественный способ маркировки θ = arg (z) в этом примере установить −π < θ ≤ π на первом листе с π < θ ≤ 3π на второй. Воображаемые оси на двух листах направлены в противоположные стороны, так что направление положительного вращения против часовой стрелки сохраняется, когда замкнутый контур перемещается от одного листа к другому (помните, что второй лист - это Сверху вниз). Представьте себе эту поверхность, встроенную в трехмерное пространство, причем оба листа параллельны поверхности. ху-самолет. Затем на поверхности появляется вертикальное отверстие, в котором два разреза соединяются вместе. Что делать, если разрез сделан из z = −1 вниз по действительной оси до бесконечно удаленной точки, а от z = 1вверх по реальной оси, пока разрез не встретится сам? Снова можно построить риманову поверхность, но на этот раз «дыра» горизонтальна. Топологически говоря, обе версии этой римановой поверхности эквивалентны - они ориентируемый двумерные поверхности род один.
Использование комплексной плоскости в теории управления
В теория управления, одно использование комплексной плоскости известно как 's-plane '. Он используется для графической визуализации корней уравнения, описывающего поведение системы (характеристическое уравнение). Уравнение обычно выражается полиномом от параметра s Преобразование Лапласа, отсюда и название «самолет». Точки в s-плоскости принимают вид , куда 'j' используется вместо обычного 'я' для представления мнимой составляющей.
Еще одно связанное использование комплексной плоскости с Критерий устойчивости Найквиста. Это геометрический принцип, который позволяет определить стабильность замкнутой системы обратной связи путем проверки Сюжет Найквиста амплитуды разомкнутого контура и фазовой характеристики как функции частоты (или контура функция передачи ) в комплексной плоскости.
Z-плоскость - это дискретная версия s-плоскости, где z-преобразования используются вместо преобразования Лапласа.
Квадратичные пространства
Комплексная плоскость связана с двумя различными квадратичные пространства. Для точки z = Икс + иу в комплексной плоскости функция возведения в квадрат z2 и норм-квадрат оба квадратичные формы. Первым часто пренебрегают после того, как последний используют для установки метрика на комплексной плоскости. Эти различные грани комплексной плоскости как квадратичного пространства возникают при построении алгебры над полем с Процесс Кэли-Диксона. Эту процедуру можно применить к любому поле, и для полей и получаются разные результаты: если ℝ - поле взлета, то ℂ строится с квадратичной формой но процесс также может начинаться с ℂ и z2, и этот случай порождает алгебры, отличные от алгебр, полученных из. В любом случае порождаемые алгебры композиционные алгебры; в этом случае комплексная плоскость является точкой для двух различных композиционных алгебр.
Другие значения слова «комплексная плоскость»
В предыдущих разделах этой статьи комплексная плоскость рассматривается с точки зрения геометрического представления комплексных чисел.Хотя такое использование термина «комплексная плоскость» имеет долгую и богатую математически историю, это ни в коем случае не единственное математическое понятие, которое можно охарактеризовать как «комплексная плоскость». Есть как минимум три дополнительных возможности.
- Двумерное комплексное векторное пространство, «комплексная плоскость» в том смысле, что это двумерное векторное пространство, координаты которого равны сложные числа. Смотрите также: Комплексное аффинное пространство § Два измерения.
- (1 + 1) -мерный Пространство Минковского, также известный как расщепленная комплексная плоскость, является «комплексной плоскостью» в том смысле, что алгебраическая разделенные комплексные числа можно разделить на две реальные составляющие, которые легко ассоциируются с точкой (Икс, у) в декартовой плоскости.
- Набор двойные числа над реалами также можно поставить во взаимно однозначное соответствие с точками (Икс, у) декартовой плоскости, и представляют собой еще один пример «комплексной плоскости».
Терминология
Хотя терминология «сложная плоскость» является исторически принятой, объект можно было бы более уместно назвать «сложная линия», поскольку он является одномерным. комплексное векторное пространство.
Смотрите также
Примечания
- ^ Хотя это наиболее распространенное математическое значение фразы «комплексная плоскость», это не единственно возможное. Альтернативы включают расщепленная комплексная плоскость и двойные числа, как введено кольца частных.
- ^ Подробное определение сложного аргумента в терминах полный арктангенс можно найти в описании функции atan2.
- ^ Все знакомые свойства комплексной экспоненциальной функции, тригонометрических функций и комплексного логарифма можно вывести непосредственно из степенной ряд за . В частности, основная ценность , куда , можно рассчитать без привязки к геометрическим или тригонометрическим конструкциям.[1]
- ^ Мемуары Весселя были представлены Датской академии в 1797 году; Статья Аргана была опубликована в 1806 году.[4]
- ^ Смотрите также Доказательство аналитичности голоморфных функций.
- ^ Бесконечное произведение для Γ (z) является равномерно сходящийся на любой ограниченной области, где ни один из знаменателей не обращается в нуль; следовательно, он определяет мероморфную функцию на комплексной плоскости.[7]
- ^ Когда Re (z)> 0 эта сумма сходится равномерно на любой ограниченной области по сравнению с ζ(2), где ζ(s) это Дзета-функция Римана.
Рекомендации
- ^ Видеть (Уиттакер и Ватсон, 1927 г. ), Приложение.
- ^ Видеть (Уиттакер и Ватсон, 1927 г. ), п. 10.
- ^ В., Вайсштейн, Эрик. «Диаграмма Аргана». mathworld.wolfram.com. Получено 19 апреля 2018.
- ^ Видеть (Уиттакер и Ватсон, 1927 г. ), п. 9.
- ^ Видеть (Фланиган 1983 ), п. 305.
- ^ а б Видеть (Моретти 1964 ), С. 113–119.
- ^ Видеть (Уиттакер и Ватсон, 1927 г. ), стр. 235–236.
- ^ Видеть (Стена 1948 г. ), п. 39.
Процитированные работы
- Фланиган, Фрэнсис Дж. (1983). Комплексные переменные: гармонические и аналитические функции. Дувр. ISBN 0-486-61388-7.
- Моретти, Джино (1964). Функции комплексной переменной. Прентис-Холл.
- Уолл, Х.С. (1948). Аналитическая теория непрерывных дробей. Компания Д. Ван Ностранд. Перепечатано (1973) издательством Chelsea Publishing Company ISBN 0-8284-0207-8.
- Уиттакер, Э. Т.; Уотсон, Г.Н. (1927). Курс современного анализа (Четвертое изд.). Издательство Кембриджского университета.
внешняя ссылка
- Вайсштейн, Эрик В. «Диаграмма Аргана». MathWorld.
- Жан-Робер Арган, "Essai sur une manière de représenter des Quantités Imminaires dans les constructions géométriques", 1806 г., онлайн, анализ BibNum [для английской версии нажмите "à télécharger"]











![Gamma (z) = { frac {e ^ {- gamma z}} {z}} prod _ {n = 1} ^ { infty} left [ left (1 + { frac {z}) {n}} right) ^ {- 1} e ^ {z / n} right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/78a2a4c26802856b410866a0e00e4c5046664928)











