Тригонометрические функции - Trigonometric functions
| Тригонометрия |
|---|
 |
| Ссылка |
| Законы и теоремы |
| Исчисление |

В математика, то тригонометрические функции (также называемый круговые функции, угловые функции или же гониометрические функции[1][2]) находятся реальные функции которые относятся к углу прямоугольный треугольник соотношениям двух сторон. Они широко используются во всех науках, связанных с геометрия, Такие как навигация, механика твердого тела, небесная механика, геодезия, и много других. Они одни из самых простых периодические функции, и как таковые также широко используются для изучения периодических явлений с помощью Анализ Фурье.
Тригонометрические функции, наиболее широко используемые в современной математике, - это синус, то косинус, а касательная. Их взаимные соответственно косеканс, то секущий, а котангенс, которые реже используются. Каждая из этих шести тригонометрических функций имеет соответствующую обратную функцию (называемую обратная тригонометрическая функция ), и эквивалент в гиперболические функции также.[3]
Самые старые определения тригонометрических функций, относящиеся к прямоугольным треугольникам, определяют их только для острые углы. Чтобы распространить эти определения на функции, домен это весь проективно расширенная действительная линия, геометрические определения с использованием стандарта единичный круг (т.е. круг с радиус 1 ед.). Современные определения выражают тригонометрические функции как бесконечная серия или как решения дифференциальные уравнения. Это позволяет расширить область синусоидальных и косинусоидальных функций на всю комплексная плоскость, а область определения остальных тригонометрических функций на комплексную плоскость (из которой удалены некоторые изолированные точки).
Определения прямоугольного треугольника
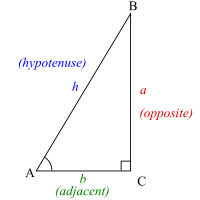

В этом разделе одна и та же заглавная буква обозначает вершину треугольника и меру соответствующего угла; та же строчная буква обозначает край треугольника и его длину.
Учитывая острый угол А = θ из прямоугольный треугольник, то гипотенуза час сторона, соединяющая два острых угла. Сторона б соседний к θ сторона треугольника, соединяющего θ под прямым углом. Третья сторона а как говорят противоположный к θ.
Если угол θ задано, то все стороны прямоугольного треугольника равны четко определенный с точностью до коэффициента масштабирования. Это означает, что соотношение любых двух длин сторон зависит только от θ. Таким образом, эти шесть соотношений определяют шесть функций θ, которые являются тригонометрическими функциями. Точнее, шесть тригонометрических функций:[4][5]
- синус
- косинус
- касательная
- косеканс
- секущий
- котангенс
В прямоугольном треугольнике сумма двух острых углов составляет прямой угол, то есть 90 ° или радианы.
| Функция | Сокращение | Описание | Отношение | |
|---|---|---|---|---|
| с помощью радианы | с помощью градусы | |||
| синус | грех | противоположный/гипотенуза | ||
| косинус | потому что | соседний/гипотенуза | ||
| касательная | загар (или тг) | противоположный/соседний | ||
| котангенс | детская кроватка (или котан, или котг, или ctg, или ctn) | соседний/противоположный | ||
| секущий | сек | гипотенуза/соседний | ||
| косеканс | csc (или cosec) | гипотенуза/противоположный | ||

Нижний: График зависимости синусоиды от угла. Идентифицируются углы от верхней панели.
Радианы против градусов
Эта секция не цитировать любой источники. (Август 2020 г.) (Узнайте, как и когда удалить этот шаблон сообщения) |
В геометрических приложениях аргумент тригонометрической функции обычно является мерой угол. Для этого любой угловая единица удобен, а углы обычно измеряются в градусы (особенно в элементарная математика ).
При использовании тригонометрической функции в исчисление, их аргумент - обычно не угол, а настоящий номер. В этом случае более целесообразно выразить аргумент тригонометрии как длину дуга из единичный круг - ограничен углом, вершиной которого является центр окружности. Поэтому используется радиан как угловая единица: радиан - это угол, ограничивающий дугу длины 1 на единичном круге. Полный повернуть таким образом, угол 2π радианы.
Большим преимуществом радианов является то, что они упрощают формулирование многих формул, обычно все формулы относительно производные и интегралы.
Из-за этого часто понимается, что, когда угловая единица не указана явно, аргументы тригонометрических функций всегда выражаются в радианах..[7]
Определения единичного круга


Шесть тригонометрических функций можно определить как значения координат точек на Евклидова плоскость которые связаны с единичный круг, какой круг радиуса один с центром в начале координат О этой системы координат. Пока определения прямоугольного треугольника позволяет определять тригонометрические функции для углов между 0 и радиан (90°), определения единичного круга позволяют расширить область тригонометрических функций на все положительные и отрицательные действительные числа.
Вращая луч со стороны положительной половины Икс-ось под углом θ (против часовой стрелки за и по часовой стрелке для ) дает точки пересечения этого луча (см. рисунок) с единицей круг: , и, если необходимо, продолжив луч до линии, линия и с линия Касательная к единичной окружности в точке А, ортогональный этому лучу, пересекает у- и Икс-оси в точках и . Значения координат этих точек дают все существующие значения тригонометрических функций для произвольных действительных значений θ следующим образом.
Тригонометрические функции потому что и грех определяются соответственно как Икс- и у-координатные значения точки А. То есть,
- и [9]
В диапазоне , это определение совпадает с определением прямоугольного треугольника, если принять прямоугольный треугольник с единичным радиусом OA в качестве гипотенуза. А поскольку уравнение справедливо для всех точек на единичной окружности это определение косинуса и синуса также удовлетворяет Пифагорейская идентичность
Остальные тригонометрические функции можно найти вдоль единичной окружности как
- и
- и
Применяя методы пифагорейского тождества и геометрического доказательства, можно легко показать, что эти определения совпадают с определениями тангенса, котангенса, секанса и косеканса в терминах синуса и косинуса, т. Е.

Поскольку поворот на угол не меняет положение или размер фигуры, точки А, B, C, D, и E одинаковы для двух углов, разность которых кратна целому числу . Таким образом, тригонометрические функции периодические функции с периодом . То есть равенства
- и
держать под любым углом θ и любой целое число k. То же самое и с четырьмя другими тригонометрическими функциями. Наблюдая за знаком и монотонностью функций синуса, косинуса, косеканса и секанса в четырех квадрантах, можно показать, что 2π - наименьшее значение, для которого они периодичны (т. е. 2π это основной период этих функций). Однако после поворота на угол , точки B и C уже возвращаются в исходное положение, так что функция тангенса и функция котангенса имеют основной период π. То есть равенства
- и
держать под любым углом θ и любое целое число k.
Алгебраические значения

В алгебраические выражения для наиболее важных углов следующие:
- (прямой угол )
- (прямой угол )
Запись числителей в виде квадратных корней последовательных неотрицательных целых чисел со знаменателем 2 обеспечивает простой способ запоминания значений.[10]
Такие простые выражения обычно не существуют для других углов, которые являются рациональными кратными прямому углу. Для угла, который, измеренный в градусах, кратен трем, синус и косинус могут быть выражены через квадратные корни, видеть Тригонометрические константы, выраженные в действительных радикалах. Таким образом, эти значения синуса и косинуса могут быть построены с помощью линейка и компас.
Для угла, равного целому числу градусов, синус и косинус могут быть выражены через квадратные корни и кубический корень ненастоящего комплексное число. Теория Галуа позволяет доказать, что, если угол не кратен 3 °, ненастоящие кубические корни неизбежны.
Для угла, который измеряется в градусах, Рациональное число, синус и косинус равны алгебраические числа, который может быть выражен через пкорни. Это связано с тем, что Группы Галуа из циклотомические многочлены находятся циклический.
Для угла, который измеряется в градусах, не является рациональным числом, тогда либо угол, либо и синус, и косинус равны трансцендентные числа. Это следствие Теорема Бейкера, доказано в 1966 году.
Простые алгебраические значения
В следующей таблице приведены простейшие алгебраические значения тригонометрических функций.[11] Символ ∞ представляет точка в бесконечности на проективно расширенная действительная линия; он не подписан, потому что, когда он появляется в таблице, соответствующая тригонометрическая функция стремится к +∞ с одной стороны, и чтобы –∞ с другой стороны, когда аргумент стремится к значению в таблице.
В исчислении



Тригонометрические функции дифференцируемый. Это не сразу видно из приведенных выше геометрических определений. Более того, современная тенденция в математике - построение геометрия из исчисление а не наоборот[нужна цитата ]. Поэтому, за исключением очень элементарного уровня, тригонометрические функции определяются с использованием методов исчисления.
Для определения тригонометрических функций внутри исчисления есть две эквивалентные возможности, либо с помощью степенной ряд или же дифференциальные уравнения. Эти определения эквивалентны, поскольку, начиная с одного из них, легко получить другое как свойство. Однако определение через дифференциальные уравнения в чем-то более естественное, так как, например, выбор коэффициентов степенного ряда может показаться совершенно произвольным, и Пифагорейская идентичность намного проще вывести из дифференциальных уравнений.
Определение дифференциальными уравнениями
Синус и косинус - уникальные дифференцируемые функции такой, что
Дифференцируя эти уравнения, мы получаем, что и синус, и косинус являются решениями дифференциальное уравнение
Применяя правило частного к определению касательной как отношения синуса к косинусу, получаем, что функция касательной проверяет
Расширение серии Power
Применяя дифференциальные уравнения к степенной ряд с неопределенными коэффициентами можно вывести повторяющиеся отношения для коэффициентов при Серия Тейлор функций синуса и косинуса. Эти рекуррентные соотношения легко решаются и дают разложения в ряды[12]
В радиус схождения этих серий бесконечно. Следовательно, синус и косинус можно продолжить до целые функции (также называемые "синус" и "косинус"), которые (по определению) комплексные функции которые определены и голоморфный в целом комплексная плоскость.
Будучи определенными как доли целых функций, другие тригонометрические функции могут быть расширены до мероморфные функции, то есть функции, голоморфные во всей комплексной плоскости, за исключением некоторых изолированных точек, называемых полюса. Здесь полюса - это числа вида для касательной и секущей, или для котангенса и косеканса, где k - произвольное целое число.
Соотношения рекуррентности также могут быть вычислены для коэффициентов Серия Тейлор других тригонометрических функций. Эти серии имеют конечную радиус схождения. Их коэффициенты имеют комбинаторный интерпретация: они перечисляют чередующиеся перестановки конечных множеств.[13]
Точнее, определяя
- Uп, то пth номер вверх / вниз,
- Bп, то пth Число Бернулли, и
- Eп, это пth Число Эйлера,
one имеет следующие расширения серий:[14]
Частичное расширение фракции
Существует представление серии как частичное расширение фракции где только что перевели взаимные функции суммируются, так что полюса функции котангенса и обратных функций совпадают:[15]
Эта идентичность может быть подтверждена с помощью Herglotz обманывать.[16]Объединение (–п)й с пй срок привести к абсолютно сходящийся серии:
Точно так же можно найти частичное разложение для секущих, косекансных и касательных функций:
Бесконечное расширение продукта
Следующее бесконечное произведение для синуса имеет большое значение в комплексном анализе:
Для доказательства этого разложения см. Синус. Отсюда можно сделать вывод, что
Связь с экспоненциальной функцией (формула Эйлера)

Формула Эйлера связывает синус и косинус с экспоненциальная функция:
Эта формула обычно рассматривается для реальных значений Икс, но это остается верным для всех сложных значений.
Доказательство: Позволять и Надо за j = 1, 2. В правило частного означает, таким образом, что . Следовательно, - постоянная функция, равная 1, так как Это доказывает формулу.
Надо
Решение этого линейная система в синусе и косинусе их можно выразить через экспоненциальную функцию:
Когда Икс реально, это можно переписать как
Наиболее тригонометрические тождества можно доказать, выразив тригонометрические функции через комплексную экспоненциальную функцию, используя приведенные выше формулы, а затем используя тождество для упрощения результата.
Определения с использованием функциональных уравнений
Можно также определить тригонометрические функции, используя различные функциональные уравнения.
Например,[17] синус и косинус образуют уникальную пару непрерывные функции которые удовлетворяют разностной формуле
и добавленное условие
В комплексной плоскости
Синус и косинус комплексное число можно выразить через действительные синусы, косинусы и гиперболические функции следующее:
Воспользовавшись раскраска домена, можно изобразить тригонометрические функции как комплексные функции. На графике можно увидеть различные особенности, уникальные для сложных функций; например, функции синуса и косинуса можно рассматривать как неограниченные, поскольку мнимая часть становится больше (поскольку белый цвет представляет бесконечность), и тот факт, что функции содержат простые нули или полюсы Это очевидно из того факта, что оттенок циклически повторяется вокруг каждого нуля или полюса ровно один раз. Сравнение этих графиков с графиками соответствующих гиперболических функций подчеркивает взаимосвязь между ними.
 |  |  |  |  |  |
Основные личности
Много идентичности связывают тригонометрические функции. В этом разделе собраны самые основные; для получения дополнительной информации см. Список тригонометрических тождеств. Эти тождества могут быть доказаны геометрически из определений единичного круга или определений прямоугольного треугольника (хотя для последних определений необходимо учитывать углы, которые не находятся в интервале [0, π/2], видеть Доказательства тригонометрических тождеств ). Для негеометрических доказательств с использованием только инструментов исчисление, можно напрямую использовать дифференциальные уравнения, аналогично тому, как это делается для выше доказательства тождества Эйлера. Можно также использовать тождество Эйлера для выражения всех тригонометрических функций в терминах комплексных экспонент и с использованием свойств экспоненциальной функции.
Паритет
Косинус и секанс равны четные функции; другие тригонометрические функции нечетные функции. То есть:
Периоды
Все тригонометрические функции периодические функции периода 2π. Это наименьший период, за исключением тангенса и котангенса, которые имеют π как наименьший период. Это означает, что для каждого целого числа k, надо
Пифагорейская идентичность
В Пифагорейская идентичность, является выражением теорема Пифагора в терминах тригонометрических функций. это
Формулы суммы и разности
Формулы суммы и разности позволяют разложить синус, косинус и тангенс суммы или разницы двух углов на синусы и косинусы и тангенсы самих углов. Их можно получить геометрически, используя аргументы, относящиеся к Птолемей. Их также можно получить алгебраически, используя Формула Эйлера.
- Сумма
- Разница
Когда два угла равны, формулы суммы сводятся к более простым уравнениям, известным как формулы двойного угла.
Эти идентичности можно использовать для получения идентичности продукта к сумме.
Установив и это позволяет выразить все тригонометрические функции как рациональная дробь из :
Вместе с
это замена касательного полуугла, что позволяет сократить вычисление интегралы и первообразные тригонометрических функций к рациональным дробям.
Производные и первообразные
В производные тригонометрических функций получаются из синуса и косинуса путем применения правило частного. Значения, указанные для первообразные в следующей таблице можно проверить, дифференцируя их. НомерC это постоянная интеграции.
Обратные функции
Тригонометрические функции периодичны и, следовательно, не инъективный, так что, строго говоря, у них нет обратная функция. Однако на каждом интервале, на котором выполняется тригонометрическая функция монотонный, можно определить обратную функцию, и это определяет обратные тригонометрические функции как многозначные функции. Чтобы определить истинную обратную функцию, необходимо ограничить область действия интервалом, в котором функция является монотонной, и, следовательно, биективный от этого интервала к его изображению функцией. Обычный выбор для этого интервала, называемый набором основные ценности, приведено в следующей таблице. Как правило, обратные тригонометрические функции обозначаются префиксом «дуга» перед названием или его сокращением.
Обозначения грешат−1, потому что−1, и т. д. часто используются для arcsin, arccos и т. д. При использовании этой нотации обратные функции можно спутать с мультипликативными обратными. Обозначение с префиксом "arc" позволяет избежать такой путаницы, хотя "arcsec" для arcsecant можно спутать с "угловая секунда ".
Так же, как синус и косинус, обратные тригонометрические функции также могут быть выражены в виде бесконечных рядов. Они также могут быть выражены через комплексные логарифмы. Видеть Обратные тригонометрические функции для подробностей.
Приложения
Углы и стороны треугольника
В этом разделе А, B, C обозначают три (внутренние) угла треугольника, а а, б, c обозначают длины соответствующих противоположных краев. Они связаны различными формулами, названными по тригонометрическим функциям, которые они включают.
Закон синусов
В закон синуса утверждает, что для произвольного треугольника со сторонами а, б, и c и углы напротив этих сторон А, B и C:
куда Δ площадь треугольника, или, что то же самое,
куда р это треугольник по окружности.
Это можно доказать, разделив треугольник на два правильных и используя приведенное выше определение синуса. Закон синусов полезен для вычисления длин неизвестных сторон треугольника, если известны два угла и одна сторона. Это обычная ситуация, возникающая в триангуляция, метод определения неизвестных расстояний путем измерения двух углов и доступного замкнутого расстояния.
Закон косинусов
В закон косинусов (также известная как формула косинуса или правило косинуса) является расширением теорема Пифагора:
или эквивалентно,
В этой формуле угол при C напротив стороныc. Эту теорему можно доказать, разделив треугольник на два прямоугольных и используя теорема Пифагора.
Закон косинусов можно использовать для определения стороны треугольника, если известны две стороны и угол между ними. Его также можно использовать для нахождения косинусов угла (и, следовательно, самих углов), если известны длины всех сторон.
Закон касательных
Следующее все формирует закон касательных[18]
Объяснение формул на словах было бы громоздким, но схемы сумм и разностей для длин и соответствующих противоположных углов очевидны в теореме.
Закон котангенсов
Если
- (радиус вписанной окружности для треугольника)
и
- (полупериметр треугольника),
то следующие все образуют закон котангенсов[18]
Следует, что
На словах теорема такова: котангенс полуугла равен отношению полупериметра минус противоположная сторона к указанному углу и внутреннему радиусу треугольника.

Периодические функции


Тригонометрические функции также важны в физике. Функции синуса и косинуса, например, используются для описания простые гармонические колебания, который моделирует многие природные явления, такие как движение массы, прикрепленной к пружине, и, для малых углов, маятниковое движение массы, подвешенной на веревке. Функции синуса и косинуса являются одномерными проекциями равномерное круговое движение.
Тригонометрические функции также оказываются полезными при изучении общих периодические функции. Характерные волновые структуры периодических функций полезны для моделирования повторяющихся явлений, таких как звук или свет. волны.[19]
При достаточно общих условиях периодическая функция ж(Икс) можно выразить как сумму синусоидальных или косинусоидальных волн в Ряд Фурье.[20] Обозначая синус или косинус базисные функции к φk, разложение периодической функции ж(т) принимает форму:
Например, прямоугольная волна можно записать как Ряд Фурье
На анимации прямоугольной волны вверху справа можно увидеть, что всего несколько членов уже дают довольно хорошее приближение. Суперпозиция нескольких членов в разложении пилообразная волна показаны внизу.
История
В то время как раннее изучение тригонометрии можно проследить до древности, тригонометрические функции в том виде, в котором они используются сегодня, были разработаны в средневековый период. В аккорд функция была обнаружена Гиппарх из Никее (180–125 до н. Э.) И Птолемей из Римский Египет (90–165 гг. Н. Э.). Функции синуса и Версина (1 - косинус) можно проследить до джья и Коти-джья функции, используемые в Период Гупта Индийская астрономия (Арьябхатия, Сурья Сиддханта ) путем перевода с санскрита на арабский, а затем с арабского на латынь.[21] (Видеть Таблица синусов Арьябхаты.)
Все шесть используемых в настоящее время тригонометрических функций были известны в Исламская математика к 9 веку, как и закон синуса, используется в решение треугольников.[22] За исключением синуса (который был заимствован из индийской математики), персидскими математиками были открыты другие пять современных тригонометрических функций, включая косинус, тангенс, котангенс, секанс и косеканс.[22] Аль-Хваризми (ок. 780–850) создал таблицы синусов, косинусов и тангенсов. Около 830, Хабаш аль-Хасиб аль-Марвази открыл котангенс и составил таблицы касательных и котангенсов.[23][24] Мухаммад ибн Джабир аль-Харрани аль-Баттани (853–929) открыли взаимные функции секанса и косеканса и создали первую таблицу косекансов для каждого градуса от 1 ° до 90 °.[24] Позднее тригонометрические функции изучались математиками, в том числе Омар Хайям, Бхаскара II, Насир ад-Дин ат-Туси, Джамшид аль-Каши (14 век), Улугбека (14 век), Региомонтан (1464), Ретикус, и ученица Ретикуса Валентин Отон.
Мадхава Сангамаграмы (ок. 1400 г.) сделал первые шаги в анализ тригонометрических функций через бесконечная серия.[25] (Видеть Серия Мадхава и Таблица синусов Мадхавы.)
Условия касательная и секущий были впервые представлены Датский математик Томас Финке в его книге Geometria rotundi (1583).[26]
В 16-ый век Французский математик Альбер Жирар впервые использовала аббревиатуры грех, потому что, и загар в его книге Trigonométrie.[27]
В статье, опубликованной в 1682 г., Лейбниц доказал, что грех Икс не является алгебраическая функция из Икс.[28] Хотя представлены как отношения сторон прямоугольный треугольник, и, таким образом, кажется рациональные функции, Результат Лейбница установил, что они действительно трансцендентные функции их аргумента. Задача усвоения круговых функций в алгебраические выражения была решена Эйлером в его работе. Введение в анализ бесконечного (1748 г.). Его метод заключался в том, чтобы показать, что функции синуса и косинуса чередующийся ряд формируется из четных и нечетных членов соответственно экспоненциальный ряд. Он представил "Формула Эйлера ", а также почти современные сокращения (грех., cos., запах, детская кроватка., сек., и cosec.).[21]
Некоторые функции были обычными исторически, но сейчас используются редко, например аккорд, то Версина (который появился в самых ранних таблицах[21]), Coverine, то гаверсин,[29] то эксцентричный и excosecant. В список тригонометрических тождеств показывает больше отношений между этими функциями.
- crd (θ) = 2 грех (θ/2)
- Версин (θ) = 1 - cos (θ) = 2 греха2(θ/2)
- покрывает (θ) = 1 - грех (θ) = версия (π/2 − θ)
- хаверсин (θ) = 1/2Версин (θ) = грех2(θ/2)
- exsec (θ) = сек (θ) − 1
- исключая (θ) = exsec (π/2 − θ) = csc (θ) − 1
Этимология
Слово синус происходит[30] из латинский синус, что означает «изгиб; залив», а точнее «свисающая складка верхней части тога "," грудь одежды ", который был выбран в качестве перевода того, что интерпретировалось как арабское слово jaib, что означает «карман» или «складка» в переводах произведений XII века Аль-Баттани и аль-Хваризми в Средневековая латынь.[31]Выбор был основан на неправильном прочтении арабской письменной формы. j-y-b (جيب), который сам возник как транслитерация с санскрита джива, который вместе со своим синонимом джья (стандартный санскритский термин для синуса) переводится как «тетива», что, в свою очередь, заимствовано из Древнегреческий χορδή "нить".[32]
Слово касательная происходит от латинского тангенс что означает "касание", поскольку линия касается круг единичного радиуса, тогда как секущий происходит от латинского секанс- «резка» - с линии порезы круг.[33]
Префикс "со- "(в" косинусе "," котангенсе "," косекансе ") находится в Эдмунд Гюнтер с Canon triangulorum (1620), который определяет косинус как сокращение от пазухи дополнительные (синус дополнительный угол ) и переходит к определению котангены по аналогии.[34][35]
Смотрите также
- Все студенты сдают расчет - мнемоника для вызова знаков тригонометрических функций в определенном квадранте декартовой плоскости
- Формула приближения синуса Бхаскары I.
- Дифференциация тригонометрических функций
- Обобщенная тригонометрия
- Создание тригонометрических таблиц
- Гиперболическая функция
- Список интегралов от тригонометрических функций
- Список периодических функций
- Список тригонометрических тождеств
- Полярный синус - обобщение на углы при вершинах
- Доказательства тригонометрических тождеств
- Версина - для нескольких менее используемых тригонометрических функций
Примечания
- ^ Кляйн, Кристиан Феликс (1924) [1902]. Elementarmathematik vom höheren Standpunkt aus: арифметика, алгебра, анализ (на немецком). 1 (3-е изд.). Берлин: Дж. Спрингер.
- ^ Кляйн, Кристиан Феликс (2004) [1932]. Элементарная математика с продвинутой точки зрения: арифметика, алгебра, анализ. Перевод Хедрика, Э. Р .; Ноубл, К. А. (Перевод 3-го немецкого изд.). Dover Publications, Inc. / Компания Macmillan. ISBN 978-0-48643480-3. В архиве из оригинала на 2018-02-15. Получено 2017-08-13.
- ^ «Исчерпывающий список символов алгебры». Математическое хранилище. 2020-03-25. Получено 2020-08-29.
- ^ Проттер и Морри (1970, с. АПП-2, АПП-3)
- ^ «Синус, косинус, касательная». www.mathsisfun.com. Получено 2020-08-29.
- ^ Проттер и Морри (1970, п. APP-7)
- ^ Спивак, Майкл (1967). Исчисление. Эддисон-Уэсли. С. Ch 15, PP 256-257. LCCN 67-20770.
- ^ Хэн, Ченг и Тальберт, «Дополнительная математика» В архиве 2015-03-20 на Wayback Machine, стр. 228
- ^ Битюцков, В. (07.02.2011). «Тригонометрические функции». Энциклопедия математики. В архиве из оригинала от 29.12.2017. Получено 2017-12-29.
- ^ Ларсон, Рон (2013). Тригонометрия (9-е изд.). Cengage Learning. п. 153. ISBN 978-1-285-60718-4. В архиве из оригинала от 15.02.2018. Отрывок страницы 153 В архиве 2018-02-15 в Wayback Machine
- ^ Абрамовиц, Милтон и Ирен А. Стегун, стр. 74
- ^ См. Альфорс, стр. 43–44.
- ^ Стэнли, Перечислительная комбинаторика, Том I., с. 149
- ^ Абрамовиц; Вайштайн.
- ^ Айгнер, Мартин; Циглер, Гюнтер М. (2000). Доказательства из КНИГИ (Второе изд.). Springer-Verlag. п. 149. ISBN 978-3-642-00855-9. В архиве из оригинала от 08.03.2014.
- ^ Реммерт, Рейнхольд (1991). Теория сложных функций. Springer. п. 327. ISBN 978-0-387-97195-7. В архиве из оригинала от 20.03.2015. Отрывок страницы 327 В архиве 2015-03-20 на Wayback Machine
- ^ Каннаппан, Паланиаппан (2009). Функциональные уравнения и неравенства с приложениями. Springer. ISBN 978-0387894911.
- ^ а б Универсальная энциклопедия математики, Справочные книги, 1976, стр. 529–530. Английская версия Джордж Аллен и Анвин, 1964. Перевод с немецкой версии Meyers Rechenduden, 1960.
- ^ Фарлоу, Стэнли Дж. (1993). Уравнения в частных производных для ученых и инженеров (Перепечатка изд. Wiley 1982 г.). Courier Dover Publications. п. 82. ISBN 978-0-486-67620-3. В архиве из оригинала от 20.03.2015.
- ^ См. Например, Фолланд, Джеральд Б. (2009). «Сходимость и полнота». Фурье-анализ и его приложения (Перепечатка Wadsworth & Brooks / Cole 1992 ed.). Американское математическое общество. С. 77 и далее. ISBN 978-0-8218-4790-9. В архиве из оригинала от 19.03.2015.
- ^ а б c Бойер, Карл Б. (1991). История математики (второе изд.). John Wiley & Sons, Inc. ISBN 0-471-54397-7, п. 210.
- ^ а б Джинджерич, Оуэн (1986). «Исламская астрономия». Scientific American. Vol. 254. с. 74. Архивировано с оригинал в 2013-10-19. Получено 2010-07-13.
- ^ Жак Сезиано, "Исламская математика", стр. 157, дюйм Селин, Хелайн; Д'Амброзио, Убиратан, ред. (2000). Математика в разных культурах: история незападной математики. Springer Science + Business Media. ISBN 978-1-4020-0260-1.
- ^ а б «тригонометрия». Британская энциклопедия.
- ^ О'Коннор, Дж. Дж .; Робертсон, Э.Ф. «Мадхава Сангамаграмы». Школа математики и статистики Университета Сент-Эндрюс, Шотландия. Архивировано из оригинал на 2006-05-14. Получено 2007-09-08.
- ^ "Биография Финке". В архиве из оригинала на 07.01.2017. Получено 2017-03-15.
- ^ О'Коннор, Джон Дж.; Робертсон, Эдмунд Ф., «Тригонометрические функции», Архив истории математики MacTutor, Сент-Эндрюсский университет.
- ^ Бурбаки, Николас (1994). Элементы истории математики. Springer.
- ^ Нильсен (1966 г., стр. xxiii – xxiv)
- ^ Англизированная форма впервые записана в 1593 году в Томас Фейл с Часовня, искусство набора номера.
- ^ Различные источники указывают на первое использование синус либо
- Платон Тибуртин 1116 перевод Астрономия из Аль-Баттани
- Жерар Кремоны перевод Алгебра из аль-Хваризми
- Роберт Честерский 1145 г. перевод таблиц аль-Хваризми
См. Maor (1998), глава 3, где можно найти более раннюю этимологию, в которой упоминается Джерард.
Видеть Каткс, Виктор (июль 2008 г.). История математики (3-е изд.). Бостон: Пирсон. п. 210 (боковая панель). ISBN 978-0321387004. - ^ См. Плофкер, Математика в Индии, Princeton University Press, 2009, стр. 257
Видеть "Университет Кларка". В архиве из оригинала от 15.06.2008.
Об этимологии см. Maor (1998), глава 3. - ^ Оксфордский словарь английского языка
- ^ Гюнтер, Эдмунд (1620). Canon triangulorum.
- ^ Рогель, Денис, изд. (06.12.2010). "Реконструкция треугольника канона Гюнтера (1620 г.)" (Исследовательский отчет). HAL. inria-00543938. В архиве из оригинала от 28.07.2017. Получено 2017-07-28.
Рекомендации
- Абрамовиц, Милтон; Стегун, Ирен Энн, ред. (1983) [июнь 1964]. Справочник по математическим функциям с формулами, графиками и математическими таблицами. Прикладная математика. 55 (Девятое переиздание с дополнительными исправлениями, десятое оригинальное издание с исправлениями (декабрь 1972 г.); первое издание). Вашингтон, округ Колумбия.; Нью-Йорк: Министерство торговли США, Национальное бюро стандартов; Dover Publications. ISBN 978-0-486-61272-0. LCCN 64-60036. МИСТЕР 0167642. LCCN 65-12253.
- Ларс Альфорс, Комплексный анализ: введение в теорию аналитических функций одного комплексного переменного, второе издание, Книжная компания McGraw-Hill, Нью-Йорк, 1966.
- Бойер, Карл Б., История математики, John Wiley & Sons, Inc., 2-е издание. (1991). ISBN 0-471-54397-7.
- Галь, Шмуэль и Бачелис, Борис. Точная элементарная математическая библиотека для стандарта IEEE с плавающей запятой, ACM Transactions on Mathematical Software (1991).
- Джозеф, Джордж Г., Герб Павлина: неевропейские корни математики, 2-е изд. Книги о пингвинах, Лондон. (2000). ISBN 0-691-00659-8.
- Кантабутра, Витит, «Об оборудовании для вычисления экспоненциальных и тригонометрических функций», IEEE Trans. Компьютеры 45 (3), 328–339 (1996).
- Маор, Эли, Тригонометрические наслаждения, Princeton Univ. Нажмите. (1998). Репринтное издание (2002 г.): ISBN 0-691-09541-8.
- Нидхэм, Тристан, "Предисловие" " к Визуальный комплексный анализ. Издательство Оксфордского университета, (1999). ISBN 0-19-853446-9.
- Нильсен, Кай Л. (1966), Логарифмические и тригонометрические таблицы до пяти знаков (2-е изд.), Нью-Йорк: Barnes & Noble, LCCN 61-9103
- О'Коннор, Дж. Дж. И Э. Ф. Робертсон, «Тригонометрические функции», Архив истории математики MacTutor. (1996).
- О'Коннор, Дж. Дж. И Э. Ф. Робертсон, «Мадхава Сангамаграммы», Архив истории математики MacTutor. (2000).
- Пирс, Ян Г., «Мадхава Сангамаграммы», Архив истории математики MacTutor. (2002).
- Protter, Murray H .; Морри, Чарльз Б., младший (1970), Вычисление колледжа с аналитической геометрией (2-е изд.), Литература: Эддисон-Уэсли, LCCN 76087042
- Вайсштейн, Эрик В., "Касательная" из MathWorld, по состоянию на 21 января 2006 г.
внешняя ссылка
- «Тригонометрические функции», Энциклопедия математики, EMS Press, 2001 [1994]
- Модуль Visionlearning по волновой математике
- ГониоЛаб Визуализация единичного круга, тригонометрических и гиперболических функций
- q-синус Статья о q-аналог греха в MathWorld
- q-косинус Статья о q-аналог из cos в MathWorld
























































![{displaystyle {egin {выравнивается} sin x & = x- {frac {x ^ {3}} {3!}} + {frac {x ^ {5}} {5!}} - {frac {x ^ {7} } {7!}} + Cdots [8pt] & = sum _ {n = 0} ^ {infty} {frac {(-1) ^ {n} x ^ {2n + 1}} {(2n + 1) !}} [8pt] cos x & = 1- {frac {x ^ {2}} {2!}} + {Frac {x ^ {4}} {4!}} - {frac {x ^ {6} } {6!}} + Cdots [8pt] & = sum _ {n = 0} ^ {infty} {frac {(-1) ^ {n} x ^ {2n}} {(2n)!}}. конец {выровнен}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8b96cbd9a749c461b481fbd08d70ed37ebb8efd1)























![{displaystyle {egin {выровнено} e ^ {ix} & = cos x + isin x [5pt] e ^ {- ix} & = cos x-isin x.end {выравнивается}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8d374fafbe34908c7766b67e4c51797589906940)
![{displaystyle {egin {выравнивается} sin x & = {frac {e ^ {ix} -e ^ {- ix}} {2i}} [5pt] cos x & = {frac {e ^ {ix} + e ^ {- ix}} {2}}. конец {выровнено}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/590e4a1bbe3ccdb7521fe06a6e5b56e538d4e729)





![{displaystyle {egin {выровнено} sin z & = sin xcosh y + icos xsinh y [5pt] cos z & = cos xcosh y-isin xsinh yend {выровнено}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c1646655eab602e234f42df85cae241ffbb867cf)































