Синус - Википедия - Sine

Синус
Основные характеристики
Паритет	странный
Домен	(−∞, +∞) а
Codomain	[−1, 1] а
Период	2π
Конкретные значения
На нуле	0
Максима	(2kπ + π/2, 1)б
Минимумы	(2kπ − π/2, −1)
Особенности
Корень	kπ
Критическая точка	kπ + π/2
Точка перегиба	kπ
Фиксированная точка	0
	а За настоящий числа.; б Переменная k является целое число.;

В математика, то синус это тригонометрическая функция из угол. Синус острого угла определяется в контексте прямоугольный треугольник: для указанного угла это отношение длины стороны, противоположной этому углу, к длине самой длинной стороны треугольника ( гипотенуза ). Для угла ${ displaystyle x}$ , синусоидальная функция обозначается просто как ${ Displaystyle грех х}$ .^[1]^[2]

В более общем плане определение синуса (и других тригонометрических функций) может быть распространено на любые настоящий значение в терминах длины определенного сегмента линии в единичный круг. Более современные определения выражают синус как бесконечная серия, или как решение некоторых дифференциальные уравнения, позволяя их расширение до произвольных положительных и отрицательных значений и даже до сложные числа.

Синусоидальная функция обычно используется для моделирования периодический такие явления как звук световые волны, положение и скорость гармонических осцилляторов, интенсивность солнечного света и продолжительность дня, а также средние колебания температуры в течение года.

Функцию синуса можно проследить до джья и Koṭi-jyā функции, используемые в Период Гупта Индийская астрономия (Арьябхатия, Сурья Сиддханта ) путем перевода с санскрита на арабский, а затем с арабского на латынь.^[3] Слово «синус» (лат. «Синус») происходит от латинский неправильный перевод Роберт Честерский арабского джиба, что является транслитерация санскритского слова для половины аккорда, джья-ардха.^[4]

Определение прямоугольного треугольника

Для угла αфункция синуса дает отношение длины противоположной стороны к длине гипотенузы.

Чтобы определить синусоидальную функцию острого угла α, начнем с прямоугольный треугольник который содержит угол измерения α; на сопроводительном рисунке угол α в треугольнике ABC угол интереса. Три стороны треугольника названы следующим образом:

В Обратная сторона сторона, противоположная интересующему углу, в данном случае сторонаа.
В гипотенуза сторона, противоположная прямому углу, в данном случае стороначас. Гипотенуза - это всегда самая длинная сторона прямоугольного треугольника.
В прилегающая сторона остальная сторона, в данном случае сторонаб. Он образует сторону (и примыкает) к обоим интересующим углам (углу А) и под прямым углом.

После выбора такого треугольника синус угла равен длине противоположной стороны, деленной на длину гипотенузы:^[5]

{ Displaystyle грех ( альфа) = { гидроразрыва { textrm {напротив}} { textrm {гипотенуза}}}}

Остальные тригонометрические функции угла можно определить аналогично; например, косинус угла - это отношение между смежной стороной и гипотенузой, а касательная дает соотношение между противоположной и соседней сторонами.^[5]

Как уже говорилось, значение ${ Displaystyle грех ( альфа)}$ похоже, зависит от выбора прямоугольного треугольника, содержащего угол измерения α. Однако это не так: все такие треугольники похожий, поэтому соотношение для каждого из них одинаковое.

Определение единичного круга

В тригонометрия, а единичный круг круг радиуса один с центром в начале координат (0, 0) в Декартова система координат.

Единичный круг: круг с радиусом один

Пусть прямая, проходящая через начало координат, пересекает единичную окружность, составляя угол θ с положительной половиной Икс-ось. В Икс- и у-координаты этой точки пересечения равны $cos (θ)$ и $грех (θ)$ , соответственно. Это определение согласуется с определением синуса и косинуса для прямоугольного треугольника, когда 0 ° < θ <90 °: поскольку длина гипотенузы единичной окружности всегда равна 1, ${ displaystyle sin ( theta) = { tfrac { textrm {напротив}} { textrm {hypotenuse}} = { tfrac { textrm {напротив}} {1}} = { textrm {напротив} }}$ . Длина противоположной стороны треугольника - это просто длина у-координат. Аналогичный аргумент можно привести для функции косинуса, чтобы показать, что ${ Displaystyle соз ( тета) = { tfrac { textrm {смежный}} { textrm {гипотенуза}}}}$ когда 0 ° < θ <90 °, даже при новом определении с использованием единичной окружности. $загар (θ)$ тогда определяется как ${ Displaystyle { tfrac { грех ( тета)} { соз ( тета)}}}$ , или, что то же самое, как наклон отрезка прямой.

Использование определения единичного круга имеет то преимущество, что угол может быть расширен до любого реального аргумента. Этого также можно достичь, потребовав определенной симметрии, и чтобы синус был периодическая функция.

Анимация, показывающая, как функционирует синус (красным) ${ Displaystyle у = грех ( тета)}$ построено на графике из у-координата (красная точка) точки на единичный круг (зеленым), под углом θ.

Идентичности

Точные личности (с использованием радианы ):

Они применимы для всех значений ${ displaystyle theta}$ .

{ displaystyle sin ( theta) = cos left ({ frac { pi} {2}} - theta right) = { frac {1} { csc ( theta)}}}

Взаимный

В взаимный синуса косеканс, т. е. обратный $грех (А)$ является $csc (А)$ , или cosec (А). Косеканс дает отношение длины гипотенузы к длине противоположной стороны:^[1]

{ displaystyle csc (A) = { frac {1} { sin (A)}} = { frac { textrm {hypotenuse}} { textrm {напротив}}} = { frac {h} { a}}.}

Обратный

Обычные основные значения

arcsin (Икс)

функция, построенная на декартовой плоскости. Арчин - это противоположность греху.

В обратная функция синуса - это арксинус (arcsin или asin) или обратный синус ( $грех -1$ ).^[1] Поскольку синус не-инъективный, это не точная обратная функция, а частичная обратная функция. Например, $грех (0) = 0$ , но также $грех (π) = 0$ , $грех (2 π) = 0$ и т. д. Отсюда следует, что функция арксинуса многозначна: $arcsin (0) = 0$ , но также $arcsin (0) = π$ , $arcsin (0) = 2 π$ и т. д. Если требуется только одно значение, функция может быть ограничена его главный филиал. С этим ограничением для каждого Икс в домене выражение $arcsin (Икс)$ будет оценивать только одно значение, называемое его основная стоимость.

{ displaystyle theta = arcsin left ({ frac { text {напротив}} { text {hypotenuse}}} right) = sin ^ {- 1} left ({ frac {a} { h}} right).}

где (для некоторого целого k):

{ Displaystyle { begin {align} sin (y) = x iff & y = arcsin (x) +2 pi k, { text {or}} & y = pi - arcsin (x) +2 пи к конец {выровнено}}}

Или в одном уравнении:

{ displaystyle sin (y) = x iff y = (- 1) ^ {k} arcsin (x) + pi k}

По определению арксинус удовлетворяет уравнению:

{ Displaystyle грех ( arcsin (х)) = х !}

и

{ displaystyle arcsin ( sin ( theta)) = theta quad { text {for}} - { frac { pi} {2}} leq theta leq { frac { pi} {2}}.}

Исчисление

Для синусоидальной функции:

{ Displaystyle е (х) = грех (х)}

Производная:

{ Displaystyle F '(х) = соз (х)}

Первообразная:

{ Displaystyle int е (х) , дх = - соз (х) + С}

куда C обозначает постоянная интеграции.^[2]

Другие тригонометрические функции

Функции синуса и косинуса связаны множеством способов. Две функции сдвинуты по фазе на 90 °:

{ Displaystyle грех ( пи / 2-х)}

=

{ Displaystyle соз (х)}

для всех углов Икс. Также производная функции

грех (Икс)

является

cos (Икс)

.

Любую тригонометрическую функцию можно выразить через любую другую (до знака плюс или минус или с помощью функция знака ).

В следующей таблице показано, как синус можно выразить через другие распространенные тригонометрические функции:

	ж θ	Использование плюс / минус (±)					Использование функции знака (sgn)
		ж θ =	± на квадрант				ж θ =
		ж θ =	я	II	III	IV	ж θ =
потому что	${ Displaystyle грех ( тета)}$	${ displaystyle = pm { sqrt {1- cos ^ {2} ( theta)}}}$	+	+	−	−	${ displaystyle = operatorname {sgn} left ( cos left ( theta - { frac { pi} {2}} right) right) { sqrt {1- cos ^ {2} ( theta)}}}$
потому что	${ Displaystyle соз ( тета)}$	${ displaystyle = pm { sqrt {1- sin ^ {2} ( theta)}}}$	+	−	−	+	${ displaystyle = operatorname {sgn} left ( sin left ( theta + { frac { pi} {2}} right) right) { sqrt {1- sin ^ {2} ( theta)}}}$
детская кроватка	${ Displaystyle грех ( тета)}$	${ displaystyle = pm { frac {1} { sqrt {1+ cot ^ {2} ( theta)}}}}$	+	+	−	−	${ displaystyle = operatorname {sgn} left ( cot left ({ frac { theta} {2}} right) right) { frac {1} { sqrt {1+ cot ^ { 2} ( theta)}}}}$
детская кроватка	${ displaystyle cot ( theta)}$	${ displaystyle = pm { frac { sqrt {1- sin ^ {2} ( theta)}} { sin ( theta)}}}$	+	−	−	+	${ displaystyle = operatorname {sgn} left ( sin left ( theta + { frac { pi} {2}} right) right) { frac { sqrt {1- sin ^ { 2} ( theta)}} { sin ( theta)}}}$
загар	${ Displaystyle грех ( тета)}$	${ displaystyle = pm { frac { tan ( theta)} { sqrt {1+ tan ^ {2} ( theta)}}}}$	+	−	−	+	${ displaystyle = operatorname {sgn} left ( tan left ({ frac {2 theta + pi} {4}} right) right) { frac { tan ( theta)} { sqrt {1+ tan ^ {2} ( theta)}}}}$
загар	${ Displaystyle загар ( тета)}$	${ displaystyle = pm { frac { sin ( theta)} { sqrt {1- sin ^ {2} ( theta)}}}}$	+	−	−	+	${ displaystyle = operatorname {sgn} left ( sin left ( theta + { frac { pi} {2}} right) right) { frac { sin ( theta)} { sqrt {1- sin ^ {2} ( theta)}}}}$
сек	${ Displaystyle грех ( тета)}$	${ displaystyle = pm { frac { sqrt { sec ^ {2} ( theta) -1}} { sec ( theta)}}}$	+	−	+	−	${ displaystyle = operatorname {sgn} left ( sec left ({ frac {4 theta - pi} {2}} right) right) { frac { sqrt { sec ^ {2 } ( theta) -1}} { sec ( theta)}}}$
сек	${ Displaystyle сек ( тета)}$	${ displaystyle = pm { frac {1} { sqrt {1- sin ^ {2} ( theta)}}}}$	+	−	−	+	${ displaystyle = operatorname {sgn} left ( sin left ( theta + { frac { pi} {2}} right) right) { frac {1} { sqrt {1- грех ^ {2} ( theta)}}}}$

Для всех уравнений, в которых используется плюс / минус (±), результат будет положительным для углов в первом квадранте.

Основное соотношение между синусом и косинусом также может быть выражено как Пифагорейская тригонометрическая идентичность:^[2]

{ Displaystyle соз ^ {2} ( тета) + грех ^ {2} ( тета) = 1 !}

где грех²(Икс) означает (грех (Икс))².

Функция квадрата синуса

Синусоидальная функция синего цвета и функция синус-квадрата красным. Ось Y в радианах.

На графике показаны как синусоидальная функция, так и синус в квадрате функция, с синим синусом и красным синусом в квадрате. Оба графика имеют одинаковую форму, но с разными диапазонами значений и разными периодами. Синус в квадрате имеет только положительные значения, но в два раза больше периодов.

Функция квадрата синуса может быть выражена как модифицированная синусоида из тождества Пифагора и уменьшения мощности - формулой двойного угла косинуса:^[6]

{ displaystyle sin ^ {2} ( theta) = { frac {1- sin (2 theta + { tfrac { pi} {2}})} {2}} }

Свойства, относящиеся к квадрантам

Четыре квадранта декартовой системы координат

В таблице ниже показаны многие ключевые свойства синусоидальной функции (знак, монотонность, выпуклость), упорядоченные по квадранту аргумента. Для аргументов, не указанных в таблице, можно вычислить соответствующую информацию, используя периодичность ${ Displaystyle грех ( альфа +360 ^ { circ}) = грех ( альфа)}$ синусоидальной функции.

Квадрант	Градусы	Радианы	Ценить	Знак	Монотонность	Выпуклость
1-й квадрант	${ Displaystyle 0 ^ { circ} <х <90 ^ { circ}}$	${ Displaystyle 0 <Икс <{ гидроразрыва { pi} {2}}}$	${ Displaystyle 0 < грех (х) <1}$	${ displaystyle +}$	увеличение	вогнутый
2-й квадрант	${ Displaystyle 90 ^ { circ} <х <180 ^ { circ}}$	${ Displaystyle { frac { pi} {2}} <х < pi}$	${ Displaystyle 0 < грех (х) <1}$	${ displaystyle +}$	уменьшение	вогнутый
3-й квадрант	${ Displaystyle 180 ^ { circ} <х <270 ^ { circ}}$	${ displaystyle pi$	${ Displaystyle -1 < грех (х) <0}$	${ displaystyle -}$	уменьшение	выпуклый
4-й квадрант	${ displaystyle 270 ^ { circ}$	${ Displaystyle { гидроразрыва {3 pi} {2}} <х <2 pi}$	${ Displaystyle -1 < грех (х) <0}$	${ displaystyle -}$	увеличение	выпуклый

Квадранты единичного круга и греха (Икс), с использованием Декартова система координат

В следующей таблице представлена основная информация о границах квадрантов.

Градусы	Радианы	${ Displaystyle грех (х)}$	Тип точки
${ displaystyle 0 ^ { circ}}$	${ displaystyle 0}$	${ displaystyle 0}$	Корень, Перегиб
${ displaystyle 90 ^ { circ}}$	${ displaystyle { frac { pi} {2}}}$	${ displaystyle 1}$	Максимум
${ displaystyle 180 ^ { circ}}$	${ displaystyle pi}$	${ displaystyle 0}$	Корень, Перегиб
${ displaystyle 270 ^ { circ}}$	${ displaystyle { frac {3 pi} {2}}}$	${ displaystyle -1}$	Минимум

Определение серии

Синусоидальная функция (синий) близко аппроксимируется своим Полином Тейлора степени 7 (розовый) для полного цикла с центром в исходной точке.

Эта анимация показывает, как включение все большего количества членов в частичную сумму ряда Тейлора приближается к синусоиде.

Используя только геометрию и свойства пределы, можно показать, что производная синуса является косинусом, а производная косинуса - отрицательной величиной синуса.

Использование отражения от рассчитанного геометрического вывода синуса с (4п+k) -я производная в точке 0:

{ displaystyle sin ^ {(4n + k)} (0) = { begin {cases} 0 & { text {when}} k = 0 1 & { text {when}} k = 1 0 & { text {when}} k = 2 - 1 & { text {when}} k = 3 end {case}}}

Это дает следующее разложение в ряд Тейлора при x = 0. Тогда можно использовать теорию Серия Тейлор чтобы показать, что для всех действительные числа Икс (где x - угол в радианах):^[7]

{ displaystyle { begin {align} sin (x) & = x - { frac {x ^ {3}} {3!}} + { frac {x ^ {5}} {5!}} - { frac {x ^ {7}} {7!}} + cdots [8pt] & = sum _ {n = 0} ^ { infty} { frac {(-1) ^ {n} } {(2n + 1)!}} X ^ {2n + 1} [8pt] end {выровнено}}}

Если Икс были выражены в градусах, то ряд будет содержать множители, включающие степени π / 180: если Икс это количество градусов, количество радианов у = πИкс / 180, поэтому

{ displaystyle { begin {align} sin (x _ { mathrm {deg}}) & = sin (y _ { mathrm {rad}}) & = { frac { pi} {180}} x- left ({ frac { pi} {180}} right) ^ {3} { frac {x ^ {3}} {3!}} + left ({ frac { pi} { 180}} right) ^ {5} { frac {x ^ {5}} {5!}} - left ({ frac { pi} {180}} right) ^ {7} { frac {x ^ {7}} {7!}} + cdots. end {align}}}

Формулы рядов для синуса и косинус однозначно определяются, вплоть до выбора единицы для углов, требованиями, которые

{ displaystyle { begin {align} sin (0) = 0 & { text {and}} sin (2x) = 2 sin (x) cos (x) cos ^ {2} (x ) + sin ^ {2} (x) = 1 & { text {and}} cos (2x) = cos ^ {2} (x) - sin ^ {2} (x) end { выровнено}}}

Радиан - это единица, которая приводит к разложению синуса с ведущим коэффициентом 1 и определяется дополнительным требованием:

{ displaystyle sin (x) приблизительно x { text {when}} x приблизительно 0.}

Коэффициенты как для синусоидального, так и для косинусного ряда могут быть получены путем подстановки их разложений в тождества пифагора и двойного угла, принимая старший коэффициент для синуса равным 1 и согласовывая остальные коэффициенты.

В общем, математически важные отношения между функциями синуса и косинуса и экспоненциальная функция (см., например, Формула Эйлера ) существенно упрощаются, когда углы выражаются в радианах, а не в градусах, градусах или других единицах. Поэтому в большинстве разделов математики, выходящих за рамки практической геометрии, считается, что углы выражаются в радианах.

Аналогичная серия есть Серия Григория за арктан, который получается путем опускания факториалов в знаменателе.

Непрерывная дробь

Синусоидальную функцию также можно представить в виде обобщенная цепная дробь:

{ displaystyle sin (x) = { cfrac {x} {1 + { cfrac {x ^ {2}} {2 cdot 3-x ^ {2} + { cfrac {2 cdot 3x ^ { 2}} {4 cdot 5-x ^ {2} + { cfrac {4 cdot 5x ^ {2}} {6 cdot 7-x ^ {2} + ddots}}}}}}}} .}

Представление непрерывной дроби может быть получено из Формула непрерывной дроби Эйлера и выражает настоящий номер ценности, оба рациональный и иррациональный, синусоидальной функции.

Фиксированная точка

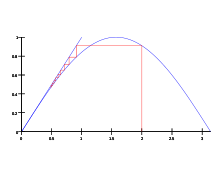
Итерация с фиксированной точкой Икс_п+1 = грех (Икс_п) с начальным значением Икс₀ = 2 сходится к 0.

Ноль - единственный настоящий фиксированная точка синусоидальной функции; другими словами, единственное пересечение синусоидальной функции и функция идентичности является sin (0) = 0.

Длина дуги

Длина дуги синусоиды между ${ displaystyle a}$ и ${ displaystyle b}$ является ${ textstyle int _ {a} ^ {b} ! { sqrt {1+ cos ^ {2} (x)}} , dx}$ .Этот интеграл является эллиптический интеграл второго рода.

Длина дуги за полный период составляет ${ textstyle { frac {4 { sqrt {2 pi ^ {3}}}} { Gamma (1/4) ^ {2}}} + { frac { Gamma (1/4) ^ { 2}} { sqrt {2 pi}}} = 7.640395578 ldots}$ куда ${ displaystyle Gamma}$ это гамма-функция.

Длина дуги синусоиды от 0 к Икс делится ли указанное выше число на ${ displaystyle 2 pi}$ раз Икс, плюс поправка, которая периодически меняется в Икс с периодом ${ displaystyle pi}$ . В Ряд Фурье для этой поправки можно записать в замкнутой форме с помощью специальных функций, но, возможно, более поучительно записать десятичные приближения коэффициентов Фурье. Длина дуги синусоиды от 0 к Икс является

{ displaystyle 1.21600672x + 0.10317093 sin (2x) -0.00220445 sin (4x) +0.00012584 sin (6x) -0.00001011 sin (8x) + cdots}

Главный член в приведенном выше уравнении и предел отношения длины дуги к расстоянию определяется выражением:

{ displaystyle { frac { pi ^ {2} +2 Gamma left ({ frac {3} {4}} right) ^ {4}} {{ sqrt {2}} pi ^ { 3/2} Gamma left ({ frac {3} {4}} right) ^ {2}}}}

Закон синусов

В закон синуса утверждает, что для произвольного треугольник с боками а, б, и c и углы напротив этих сторон А, B и C:

{ displaystyle { frac { sin A} {a}} = { frac { sin B} {b}} = { frac { sin C} {c}}.}

Это эквивалентно равенству первых трех выражений ниже:

{ displaystyle { frac {a} { sin A}} = { frac {b} { sin B}} = { frac {c} { sin C}} = 2R,}

куда р это треугольник по окружности.

Это можно доказать, разделив треугольник на два правильных и используя приведенное выше определение синуса. Закон синусов полезен для вычисления длин неизвестных сторон треугольника, если известны два угла и одна сторона. Это обычная ситуация, возникающая в триангуляция, метод определения неизвестных расстояний путем измерения двух углов и доступного замкнутого расстояния.

Особые ценности

Некоторые общие углы (θ) показано на единичный круг. Углы указаны в градусах и радианах вместе с соответствующей точкой пересечения на единичной окружности (cos (θ), грех (θ)).

Для некоторых целых чисел Икс градусов, значение греха (Икс) особенно просто. Таблица некоторых из этих значений приведена ниже.

Икс (угол)				грех (Икс)
Градусы	Радианы	Градианы	Повороты	Точный	Десятичный
0°	0	0^грамм	0	0	0
180°	π	200^грамм	1/2	0	0
15°	1/12π	16+2/3^грамм	1/24	${ displaystyle { frac {{ sqrt {6}} - { sqrt {2}}} {4}}}$	0.258819045102521
165°	11/12π	183+1/3^грамм	11/24	${ displaystyle { frac {{ sqrt {6}} - { sqrt {2}}} {4}}}$	0.258819045102521
30°	1/6π	33+1/3^грамм	1/12	1/2	0.5
150°	5/6π	166+2/3^грамм	5/12	1/2	0.5
45°	1/4π	50^грамм	1/8	${ displaystyle { frac { sqrt {2}} {2}}}$	0.707106781186548
135°	3/4π	150^грамм	3/8	${ displaystyle { frac { sqrt {2}} {2}}}$	0.707106781186548
60°	1/3π	66+2/3^грамм	1/6	${ displaystyle { frac { sqrt {3}} {2}}}$	0.866025403784439
120°	2/3π	133+1/3^грамм	1/3	${ displaystyle { frac { sqrt {3}} {2}}}$	0.866025403784439
75°	5/12π	83+1/3^грамм	5/24	${ displaystyle { frac {{ sqrt {6}} + { sqrt {2}}} {4}}}$	0.965925826289068
105°	7/12π	116+2/3^грамм	7/24	${ displaystyle { frac {{ sqrt {6}} + { sqrt {2}}} {4}}}$	0.965925826289068
90°	1/2π	100^грамм	1/4	1	1

С шагом 90 градусов:

Икс в градусах	0°	90°	180°	270°	360°
Икс в радианах	0	π / 2	π	3π / 2	2π
Икс в гонках	0	100^грамм	200^грамм	300^грамм	400^грамм
Икс по очереди	0	1/4	1/2	3/4	1
грех Икс	0	1	0	-1	0

Другие значения, не указанные выше:

{ displaystyle sin left ({ frac { pi} {60}} right) = sin (3 ^ { circ}) = { frac {(2 - { sqrt {12}}) { sqrt {5 + { sqrt {5}}}} + ({ sqrt {10}} - { sqrt {2}}) ({ sqrt {3}} + 1)} {16}}}

OEIS: A019812

{ displaystyle sin left ({ frac { pi} {30}} right) = sin (6 ^ { circ}) = { frac {{ sqrt {30 - { sqrt {180}) }}} - { sqrt {5}} - 1} {8}}}

OEIS: A019815

{ displaystyle sin left ({ frac { pi} {20}} right) = sin (9 ^ { circ}) = { frac {{ sqrt {10}} + { sqrt { 2}} - { sqrt {20 - { sqrt {80}}}}} {8}}}

OEIS: A019818

{ displaystyle sin left ({ frac { pi} {15}} right) = sin (12 ^ { circ}) = { frac {{ sqrt {10 + { sqrt {20}) }}} + { sqrt {3}} - { sqrt {15}}} {8}}}

OEIS: A019821

{ displaystyle sin left ({ frac { pi} {10}} right) = sin (18 ^ { circ}) = { frac {{ sqrt {5}} - 1} {4 }} = { tfrac {1} {2}} varphi ^ {- 1}}

OEIS: A019827

{ displaystyle sin left ({ frac {7 pi} {60}} right) = sin (21 ^ { circ}) = { frac {(2 + { sqrt {12}}) { sqrt {5 - { sqrt {5}}}} - ({ sqrt {10}} + { sqrt {2}}) ({ sqrt {3}} - 1)} {16}}}

OEIS: A019830

{ displaystyle sin left ({ frac { pi} {8}} right) = sin (22,5 ^ { circ}) = { frac { sqrt {2 - { sqrt {2}} }} {2}}}

{ displaystyle sin left ({ frac {2 pi} {15}} right) = sin (24 ^ { circ}) = { frac {{ sqrt {3}} + { sqrt {15}} - { sqrt {10 - { sqrt {20}}}}} {8}}}

OEIS: A019833

{ displaystyle sin left ({ frac {3 pi} {20}} right) = sin (27 ^ { circ}) = { frac {{ sqrt {20 + { sqrt {80) }}}} - { sqrt {10}} + { sqrt {2}}} {8}}}

OEIS: A019836

{ displaystyle sin left ({ frac {11 pi} {60}} right) = sin (33 ^ { circ}) = { frac {({ sqrt {12}} - 2) { sqrt {5 + { sqrt {5}}}} + ({ sqrt {10}} - { sqrt {2}}) ({ sqrt {3}} + 1)} {16}}}

OEIS: A019842

{ displaystyle sin left ({ frac { pi} {5}} right) = sin (36 ^ { circ}) = { frac { sqrt {10 - { sqrt {20}} }} {4}}}

OEIS: A019845

{ displaystyle sin left ({ frac {13 pi} {60}} right) = sin (39 ^ { circ}) = { frac {(2 - { sqrt {12}}) { sqrt {5 - { sqrt {5}}}} + ({ sqrt {10}} + { sqrt {2}}) ({ sqrt {3}} + 1)} {16}}}

OEIS: A019848

{ displaystyle sin left ({ frac {7 pi} {30}} right) = sin (42 ^ { circ}) = { frac {{ sqrt {30 + { sqrt {180) }}}} - { sqrt {5}} + 1} {8}}}

OEIS: A019851

Связь с комплексными числами

Иллюстрация комплексная плоскость. В мнимые числа находятся на вертикальной оси координат.

Синус используется для определения мнимая часть из комплексное число приведены в полярные координаты (р, φ):

{ Displaystyle Z знак равно р ( соз ( varphi) + я грех ( varphi))}

мнимая часть:

{ Displaystyle OperatorName {Im} (г) = г грех ( varphi)}

р и φ представляют величину и угол комплексного числа соответственно. я это мнимая единица. z это комплексное число.

Несмотря на то, что имеет дело с комплексными числами, параметр синуса в этом случае все еще является настоящий номер. Синус также может принимать в качестве аргумента комплексное число.

Синус со сложным аргументом

{ Displaystyle грех (г)}

Раскраска домена греха (z) в комплексной плоскости. Яркость указывает на абсолютную величину, насыщенность представляет собой сложный аргумент.

грех (z) как векторное поле

{ Displaystyle грех ( тета)}

мнимая часть

{ Displaystyle е ^ {я тета}}

.

Определение синусоидальной функции для сложных аргументов z:

{ displaystyle { begin {align} sin (z) & = sum _ {n = 0} ^ { infty} { frac {(-1) ^ {n}} {(2n + 1)!} } z ^ {2n + 1} & = { frac {e ^ {iz} -e ^ {- iz}} {2i}} & = { frac { sinh left (iz right) } {i}} end {выровнены}}}

куда я² = −1, а sinh равно гиперболический синус. Это вся функция. Также для чисто реальных Икс,

{ displaystyle sin (x) = operatorname {Im} (e ^ {ix}).}

Для чисто мнимых чисел:

{ Displaystyle грех (iy) = я sinh (y).}

Также иногда полезно выразить сложную синусоидальную функцию в терминах действительной и мнимой частей ее аргумента:

{ Displaystyle { begin {align} sin (x + iy) & = sin (x) cos (iy) + cos (x) sin (iy) & = sin (x) cosh (y) + i cos (x) sinh (y). end {align}}}

Частичная дробь и произведение комплексного синуса

Используя метод частичного разложения в комплексный анализ, можно найти, что бесконечный ряд

{ displaystyle { begin {align} sum _ {n = - infty} ^ { infty} { frac {(-1) ^ {n}} {zn}} = { frac {1} {z }} - 2z sum _ {n = 1} ^ { infty} { frac {(-1) ^ {n}} {n ^ {2} -z ^ {2}}} end {выровнено}} }

оба сходятся и равны ${ textstyle { frac { pi} { sin ( pi z)}}}$ . Аналогично можно показать, что

{ displaystyle { begin {align} { frac { pi ^ {2}} { sin ^ {2} ( pi z)}} = sum _ {n = - infty} ^ { infty} { frac {1} {(zn) ^ {2}}}. end {выравнивается}}}

Используя технику расширения продукта, можно получить

{ displaystyle { begin {align} sin ( pi z) = pi z prod _ {n = 1} ^ { infty} left (1 - { frac {z ^ {2}} {n ^ {2}}} right). End {align}}}

В качестве альтернативы, бесконечное произведение для синуса может быть доказано с помощью комплексный ряд Фурье.

Доказательство бесконечного произведения для синуса

Используя комплексный ряд Фурье, функция ${ Displaystyle соз (zx)}$ можно разложить как

{ displaystyle cos (zx) = { frac {z sin ( pi z)} { pi}} displaystyle sum _ {n = - infty} ^ { infty} { frac {(- 1) ^ {n} , e ^ {inx}} {z ^ {2} -n ^ {2}}}, , z in mathbb {C} setminus { mathbb {Z} } , , x in [- pi, pi].}

Параметр ${ Displaystyle х = пи}$ дает

{ displaystyle cos ( pi z) = { frac {z sin ( pi z)} { pi}} displaystyle sum _ {n = - infty} ^ { infty} { frac { 1} {z ^ {2} -n ^ {2}}} = { frac {z sin ( pi z)} { pi}} left ({ frac {1} {z ^ {2}) }} + 2 displaystyle sum _ {n = 1} ^ { infty} { frac {1} {z ^ {2} -n ^ {2}}} right).}

Поэтому получаем

{ displaystyle pi cot ( pi z) = { frac {1} {z}} + 2 displaystyle sum _ {n = 1} ^ { infty} { frac {z} {z ^ { 2} -n ^ {2}}}.}

Функция ${ displaystyle pi cot ( pi z)}$ является производной от ${ Displaystyle пер ( грех ( пи Z)) + C_ {0}}$ . Кроме того, если ${ textstyle { frac {df} {dz}} = { frac {z} {z ^ {2} -n ^ {2}}}}$ , то функция ${ displaystyle f}$ такой, что возникший ряд сходится ${ textstyle f = { frac {1} {2}} ln (1-z ^ {2} / n ^ {2}) + C_ {1}}$ , что можно доказать с помощью М-тест Вейерштрасса. Обмен суммы и производной оправдан равномерное схождение. Следует, что

{ displaystyle ln ( sin ( pi z)) = ln (z) + displaystyle sum _ {n = 1} ^ { infty} ln left (1 - { frac {z ^ { 2}} {n ^ {2}}} right) + C.}

Возведение в степень дает

{ displaystyle sin ( pi z) = ze ^ {C} displaystyle prod _ {n = 1} ^ { infty} left (1 - { frac {z ^ {2}} {n ^ { 2}}} right).}

С ${ textstyle lim _ {z to 0} { frac { sin ( pi z)} {z}} = pi}$ и ${ textstyle lim _ {z to 0} prod _ {n = 1} ^ { infty} left (1 - { frac {z ^ {2}} {n ^ {2}}} right ) = 1}$ , у нас есть ${ displaystyle e ^ {C} = pi}$ . Следовательно

{ displaystyle sin ( pi z) = pi z displaystyle prod _ {n = 1} ^ { infty} left (1 - { frac {z ^ {2}} {n ^ {2}) }}верно)}

для некоторого открытого и связного подмножества ${ Displaystyle mathbb {C}}$ . Позволять ${ displaystyle textstyle {a_ {n} (z) = - { frac {z ^ {2}} {n ^ {2}}}}}$ . С ${ displaystyle textstyle { sum _ {n = 1} ^ { infty} | a_ {n} (z) |}}$ сходится равномерно на любом замкнутом диске, ${ displaystyle textstyle { prod _ {n = 1} ^ { infty} (1 + a_ {n} (z))}}$ сходится равномерно и на любом замкнутом диске. Отсюда следует, что бесконечное произведение голоморфно на ${ Displaystyle mathbb {C}}$ . Посредством теорема тождества, бесконечное произведение для синуса справедливо для всех ${ Displaystyle г в mathbb {C}}$ , что завершает доказательство. ${ displaystyle blacksquare}$

Использование сложного синуса

грех (z) находится в функциональное уравнение для Гамма-функция,

{ Displaystyle Gamma (s) Gamma (1-s) = { pi over sin ( pi s)},}

который, в свою очередь, находится в функциональное уравнение для Дзета-функция Римана,

{ Displaystyle zeta (s) = 2 (2 pi) ^ {s-1} Gamma (1-s) sin ( pi s / 2) zeta (1-s).}

Как голоморфная функция, грех г представляет собой двумерное решение Уравнение Лапласа:

{ displaystyle Delta u (x_ {1}, x_ {2}) = 0.}

Комплексная функция синуса также связана с кривыми уровня маятники.^{[как? ]}^[8]^{[нужен лучший источник ]}

Сложные графы

**Функция синуса в комплексной плоскости**

реальный компонент	мнимая составляющая	величина

**Функция арксинуса в комплексной плоскости**

реальный компонент	мнимая составляющая	величина

История

Хотя первые исследования тригонометрии восходят к древности, тригонометрические функции поскольку они используются сегодня, были разработаны в средневековый период. В аккорд функция была обнаружена Гиппарх из Никее (180–125 до н.э.) и Птолемей из Римский Египет (90–165 гг. Н. Э.).

Функция синуса и Версина (1 - косинус) можно проследить до джья и Koṭi-jyā функции, используемые в Период Гупта (От 320 до 550 н.э.) Индийская астрономия (Арьябхатия, Сурья Сиддханта ) путем перевода с санскрита на арабский, а затем с арабского на латинский.^[3]

Все шесть используемых в настоящее время тригонометрических функций были известны в Исламская математика к 9 веку, как и закон синуса, используется в решение треугольников.^[9] За исключением синуса (который был заимствован из индийской математики), арабскими математиками были открыты другие пять современных тригонометрических функций, включая косинус, тангенс, котангенс, секанс и косеканс.^[9] Аль-Хваризми (ок. 780–850) создал таблицы синусов, косинусов и тангенсов.^[10]^[11] Мухаммад ибн Джабир аль-Харрани аль-Баттани (853–929) открыли взаимные функции секанса и косеканса и создали первую таблицу косекансов для каждого градуса от 1 ° до 90 °.^[11]

Первое опубликованное использование сокращений sin, cos и tan принадлежит французскому математику 16 века. Альбер Жирар; в дальнейшем они были обнародованы Эйлером (см. ниже). В Opus palatinum de triangulis из Георг Иоахим Ретикус, студент Коперник, вероятно, был первым в Европе, кто определил тригонометрические функции непосредственно в терминах прямоугольных треугольников, а не окружностей, с таблицами для всех шести тригонометрических функций; эта работа была закончена учеником Ретикуса Валентином Отоном в 1596 году.

В статье, опубликованной в 1682 г., Лейбниц доказал этот грех Икс не является алгебраическая функция из Икс.^[12] Роджер Котс вычислил производную синуса в его Harmonia Mensurarum (1722).^[13] Леонард Эйлер с Введение в анализин бесконечный (1748) был в основном ответственен за установление аналитического подхода к тригонометрическим функциям в Европе, также определив их как бесконечные ряды и представив "Формула Эйлера ", а также почти современные сокращения sin., cos., tang., cot., sec., и cosec.^[14]

Этимология

Этимологически, слово синус происходит от санскрит слово в аккорд, джива*(Джя его более популярный синоним). Это было транслитерированный в арабский в качестве джиба جيب, который, однако, не имеет смысла на этом языке и сокращен jb جب. Поскольку арабский язык написан без коротких гласных, «jb» интерпретировалось как слово jaib جيب, что означает «лоно». Когда в XII веке арабские тексты были переведены на латинский к Жерар Кремонский, он использовал латинский эквивалент слова "грудь", синус (что означает «грудь», «залив» или «складка»).^[15]^[16] Джерард, вероятно, был не первым ученым, использовавшим этот перевод; Роберт Честерский, кажется, предшествовал ему, и есть свидетельства более раннего использования.^[17] Английская форма синус был введен в 1590-е гг.

Программные реализации

Стандартного алгоритма вычисления синуса не существует. IEEE 754-2008, наиболее широко используемый стандарт вычислений с плавающей запятой, не касается вычисления тригонометрических функций, таких как синус.^[18] Алгоритмы вычисления синуса могут быть сбалансированы с учетом таких ограничений, как скорость, точность, переносимость или диапазон допустимых входных значений. Это может привести к разным результатам для разных алгоритмов, особенно для особых обстоятельств, таких как очень большие входные данные, например грех (10²²).

Когда-то распространенной оптимизацией программирования, особенно используемой в трехмерной графике, было предварительное вычисление таблицы значений синуса, например, одно значение на градус. Это позволяло искать результаты в таблице, а не рассчитывать их в реальном времени. С современными архитектурами ЦП этот метод не может дать никаких преимуществ.^{[нужна цитата ]}

В КОРДИК алгоритм обычно используется в научных калькуляторах.

Функция синуса, наряду с другими тригонометрическими функциями, широко доступна для разных языков программирования и платформ. В вычислениях это обычно сокращается до грех.

Некоторые архитектуры ЦП имеют встроенную инструкцию для синуса, в том числе FPU Intel x87, начиная с 80387.

В языках программирования грех обычно является либо встроенной функцией, либо находится в стандартной математической библиотеке языка.

Например, Стандартная библиотека C определяет синусоидальные функции внутри math.h: грех (двойной ), sinf (плавать ), и sinl (длинный двойной ). Параметр каждого - это плавающая точка значение, определяющее угол в радианах. Каждая функция возвращает одно и то же тип данных как он принимает. Многие другие тригонометрические функции также определены в math.h, например косинус, арксинус и гиперболический синус (sh).

По аналогии, Python определяет math.sin (x) во встроенном математика модуль. Сложные синусоидальные функции также доступны в cmath модуль, например cmath.sin (z). CPython математические функции вызывают C математика библиотеку и используйте формат с плавающей запятой двойной точности.

Реализации на основе поворотов

Некоторые программные библиотеки обеспечивают реализацию синуса с использованием входного угла пополам.повороты, пол-оборота - угол 180 градусов или ${ displaystyle pi}$ радианы. Представление углов в поворотах или полуворотах в некоторых случаях дает преимущества в точности и эффективности.^[19]^[20]

Среда	Название функции	Угловые единицы
MATLAB	`Sinpi`^[21]	пол-оборота
OpenCL	`Sinpi`^[22]	пол-оборота
р	`Sinpi`^[23]	пол-оборота
Юля	`Sinpi`^[24]	пол-оборота
CUDA	`Sinpi`^[25]	пол-оборота
РУКА	`Sinpi`^[26]	пол-оборота

Преимущество в точности проистекает из способности без потерь точно представлять ключевые углы, такие как полный оборот, полуоборот и четверть оборота в двоичной системе с плавающей запятой или с фиксированной запятой. Напротив, представляя ${ displaystyle 2 pi}$ , ${ displaystyle pi}$ , и ${ displaystyle { frac { pi} {2}}}$ в двоичной системе с плавающей запятой или двоичной шкале с фиксированной точкой всегда возникает потеря точности.

Повороты также имеют преимущество в точности и эффективности при вычислении по модулю одного периода. Вычисление по модулю 1 оборот или по модулю 2 полуоборотов может выполняться без потерь и эффективно как с плавающей, так и с фиксированной точкой. Например, вычисление по модулю 1 или 2 для значения с фиксированной запятой, масштабированного по двоичной точке, требует только битового сдвига или операции побитового И. Напротив, вычисление по модулю ${ displaystyle { frac { pi} {2}}}$ включает неточности в представлении ${ displaystyle { frac { pi} {2}}}$ .

Для приложений, связанных с датчиками угла, датчик обычно обеспечивает угловые измерения в форме, непосредственно совместимой с поворотами или полуоборотами. Например, датчик угла может отсчитывать от 0 до 4096 за один полный оборот.^[27] Если полуворота используются в качестве единицы измерения угла, тогда значение, предоставляемое датчиком, напрямую и без потерь отображается в тип данных с фиксированной точкой с 11 битами справа от двоичной точки. Напротив, если радианы используются в качестве единицы для хранения угла, то неточности и затраты на умножение необработанного целого числа датчика на приближение к ${ displaystyle { frac { pi} {2048}}}$ будет понесено.

Смотрите также

Цитаты

^ ^а ^б ^c «Исчерпывающий список символов алгебры». Математическое хранилище. 2020-03-25. Получено 2020-08-29.
^ ^а ^б ^c Вайсштейн, Эрик В. "Синус". mathworld.wolfram.com. Получено 2020-08-29.
^ ^а ^б Ута К. Мерцбах, Карл Б. Бойер (2011), История математики, Хобокен, Нью-Джерси: John Wiley & Sons, 3-е изд., Стр. 189.
^ Виктор Дж. Кац (2008), История математики, Бостон: Аддисон-Уэсли, 3-е. изд., с. 253, боковая панель 8.1. «Архивная копия» (PDF). В архиве (PDF) из оригинала на 2015-04-14. Получено 2015-04-09.CS1 maint: заархивированная копия как заголовок (связь)
^ ^а ^б «Синус, косинус, касательная». www.mathsisfun.com. Получено 2020-08-29.
^ «Функция синус-квадрат». Получено 9 августа, 2019.
^ См. Альфорс, страницы 43–44.
^ «Почему фазовый портрет простого плоского маятника и доменная окраска sin (z) так похожи?». math.stackexchange.com. Получено 2019-08-12.
^ ^а ^б Джинджерич, Оуэн (1986). «Исламская астрономия». Scientific American. Vol. 254. с. 74. Архивировано с оригинал в 2013-10-19. Получено 2010-07-13.
^ Жак Сезиано, "Исламская математика", стр. 157, дюйм Селин, Хелайн; Д'Амброзио, Убиратан, ред. (2000). Математика в разных культурах: история незападной математики. Springer Science + Business Media. ISBN 978-1-4020-0260-1.
^ ^а ^б «тригонометрия». Британская энциклопедия.
^ Николас Бурбаки (1994). Элементы истории математики. Springer.
^ "Почему у синуса простая производная В архиве 2011-07-20 на Wayback Machine ", в Исторические заметки для учителей математического анализа В архиве 2011-07-20 на Wayback Machine к В. Фредерик Рики В архиве 2011-07-20 на Wayback Machine
^ См. Merzbach, Boyer (2011).
^ Эли Маор (1998), Тригонометрические наслаждения, Princeton: Princeton University Press, стр. 35-36.
^ Виктор Дж. Кац (2008), История математики, Бостон: Аддисон-Уэсли, 3-е. изд., с. 253, боковая панель 8.1. «Архивная копия» (PDF). В архиве (PDF) из оригинала на 2015-04-14. Получено 2015-04-09.CS1 maint: заархивированная копия как заголовок (связь)
^ Смит, Д. (1958) [1925], История математики, я, Дувр, стр. 202, ISBN 0-486-20429-4
^ Большие проблемы информатики, Пол Циммерманн. 20 сентября 2006 г. - с. 14/31 «Архивная копия» (PDF). В архиве (PDF) из оригинала 2011-07-16. Получено 2010-09-11.CS1 maint: заархивированная копия как заголовок (связь)
^ "Документация MATLAB sinpi
^ "R Документация sinpi
^ "Документация MATLAB sinpi
^ "Документация по OpenCL sinpi
^ "R Документация sinpi
^ "Юлия Документация синпи
^ "Документация CUDA sinpi
^ "Документация ARM sinpi
^ "Спецификация датчика угла ALLEGRO

внешняя ссылка

СМИ, связанные с Функция синуса в Wikimedia Commons

[:0-1] а ^б ^c «Исчерпывающий список символов алгебры». Математическое хранилище. 2020-03-25. Получено 2020-08-29.

[:1-2] а ^б ^c Вайсштейн, Эрик В. "Синус". mathworld.wolfram.com. Получено 2020-08-29.

[Boyer,_Carl_B._1991_p._210-3] а ^б Ута К. Мерцбах, Карл Б. Бойер (2011), История математики, Хобокен, Нью-Джерси: John Wiley & Sons, 3-е изд., Стр. 189.

[4] Виктор Дж. Кац (2008), История математики, Бостон: Аддисон-Уэсли, 3-е. изд., с. 253, боковая панель 8.1. «Архивная копия» (PDF). В архиве (PDF) из оригинала на 2015-04-14. Получено 2015-04-09.CS1 maint: заархивированная копия как заголовок (связь)

[:2-5] а ^б «Синус, косинус, касательная». www.mathsisfun.com. Получено 2020-08-29.

[6] «Функция синус-квадрат». Получено 9 августа, 2019.

[7] См. Альфорс, страницы 43–44.

[8] «Почему фазовый портрет простого плоского маятника и доменная окраска sin (z) так похожи?». math.stackexchange.com. Получено 2019-08-12.

[Gingerich_1986-9] а ^б Джинджерич, Оуэн (1986). «Исламская астрономия». Scientific American. Vol. 254. с. 74. Архивировано с оригинал в 2013-10-19. Получено 2010-07-13.

[Sesiano-10] Жак Сезиано, "Исламская математика", стр. 157, дюйм Селин, Хелайн; Д'Амброзио, Убиратан, ред. (2000). Математика в разных культурах: история незападной математики. Springer Science + Business Media. ISBN 978-1-4020-0260-1.

[Britannica-11] а ^б «тригонометрия». Британская энциклопедия.

[12] Николас Бурбаки (1994). Элементы истории математики. Springer.

[13] "Почему у синуса простая производная В архиве 2011-07-20 на Wayback Machine ", в Исторические заметки для учителей математического анализа В архиве 2011-07-20 на Wayback Machine к В. Фредерик Рики В архиве 2011-07-20 на Wayback Machine

[boyer-14] См. Merzbach, Boyer (2011).

[15] Эли Маор (1998), Тригонометрические наслаждения, Princeton: Princeton University Press, стр. 35-36.

[16] Виктор Дж. Кац (2008), История математики, Бостон: Аддисон-Уэсли, 3-е. изд., с. 253, боковая панель 8.1. «Архивная копия» (PDF). В архиве (PDF) из оригинала на 2015-04-14. Получено 2015-04-09.CS1 maint: заархивированная копия как заголовок (связь)

[17] Смит, Д. (1958) [1925], История математики, я, Дувр, стр. 202, ISBN 0-486-20429-4

[18] Большие проблемы информатики, Пол Циммерманн. 20 сентября 2006 г. - с. 14/31 «Архивная копия» (PDF). В архиве (PDF) из оригинала 2011-07-16. Получено 2010-09-11.CS1 maint: заархивированная копия как заголовок (связь)

[19] "Документация MATLAB sinpi

[20] "R Документация sinpi

[21] "Документация MATLAB sinpi

[22] "Документация по OpenCL sinpi

[23] "R Документация sinpi

[24] "Юлия Документация синпи

[25] "Документация CUDA sinpi

[26] "Документация ARM sinpi

[27] "Спецификация датчика угла ALLEGRO

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

Тригонометрические и гиперболические функции
Элементарный	Синус Косинус Касательная
Взаимный	Косеканс Секант Котангенс
Обратный	Арксинус Арккосин Арктангенс Аркосеканс Arcsecant Арккотангенс
Гиперболический	Гиперболический синус Гиперболический косинус Гиперболический тангенс Гиперболический косеканс Гиперболический секанс Гиперболический котангенс
Обратный гиперболический	Обратный гиперболический синус Обратный гиперболический косинус Обратный гиперболический тангенс Обратный гиперболический косеканс Обратный гиперболический секанс Обратный гиперболический котангенс
Другой	Версина Гаверсин Exsecant Excosecant Джья, коти-джья и уткрама-джья atan2