Инъективная функция - Injective function

В математика, инъективная функция (также известен как инъекция, или индивидуальная функция) это функция что отображает отчетливый элементы его домен к отдельным элементам его codomain.^[1] Другими словами, каждый элемент кодомена функции является образ из в большинстве один элемент своего домена.^[2] Период, термин индивидуальная функция не следует путать с индивидуальная переписка это относится к биективные функции, которые являются такими функциями, что каждый элемент в кодомене является изображением ровно одного элемента в домене.

А гомоморфизм между алгебраические структуры - функция, совместимая с операциями структур. Для всех распространенных алгебраических структур и, в частности, для векторные пространства, инъективный гомоморфизм также называется мономорфизм. Однако в более общем контексте теория категорий, определение мономорфизма отличается от определения инъективного гомоморфизма.^[3] Таким образом, это теорема, что они эквивалентны для алгебраических структур; увидеть Гомоморфизм § Мономорфизм Больше подробностей.

Функция ж то, что не является инъективным, иногда называют «многие к одному».^[2]

Определение

Позволять ж быть функция чья домен это набор Икс. Функция ж как говорят инъективный при условии, что для всех а и б в Икс, всякий раз, когда ж(а) = ж(б), тогда а = б; это, ж(а) = ж(б) подразумевает а = б. Эквивалентно, если а ≠ б, тогда ж(а) ≠ ж(б).

Символично,

${ Displaystyle forall a, b in X, ; ; f (a) = f (b) Rightarrow a = b}$

что логически эквивалентно контрапозитивный,

${ displaystyle forall a, b in X, ; ; a neq b Rightarrow f (a) neq f (b)}$^[4][5]

Примеры

• Для любого набора Икс и любое подмножество S из Икс, то карта включения S → Икс (который отправляет любой элемент s из S себе) инъективно. В частности, функция идентичности Икс → Икс всегда инъективен (и фактически биективен).
• Если домен Икс = ∅ или Икс имеет только один элемент, то функция Икс → Y всегда инъективен.
• Функция ж : р → р определяется ж(Икс) = 2Икс + 1 инъективно.
• Функция г : р → р определяется г(Икс) = Икс² является не инъективный, потому что (например) г(1) = 1 = г(−1). Однако если г переопределяется так, что его областью определения являются неотрицательные действительные числа [0, + ∞), то г инъективно.
• В экспоненциальная функция опыт: р → р определяется ехр (Икс) = е^Икс инъективно (но не сюръективный, так как никакое действительное значение не соответствует отрицательному числу).
• В натуральный логарифм функция ln: (0, ∞) → р определяется Икс ↦ ln Икс инъективно.
• Функция г : р → р определяется г(Икс) = Икс^п − Икс не является инъективным, так как, например, г(0) = г(1) = 0.

В более общем плане, когда Икс и Y оба реальная линия р, то инъективная функция ж : р → р это тот, чей график никогда не пересекает горизонтальную линию более одного раза. Этот принцип называется проверка горизонтальной линии.^[2]

Инъективные функции. Схематическая интерпретация в Декартова плоскость, определяемый отображение ж : Икс → Y, где у = ж(Икс), Икс = область функции, Y = диапазон функций, и я(ж) обозначает образ из ж. Каждый Икс в Икс соответствует ровно одному уникальному у в Y. Части осей в кружках представляют наборы областей и диапазонов - в соответствии со стандартными диаграммами выше.

Не инъективная функция. Вот Икс₁ и Икс₂ являются подмножествами Икс, Y₁ и Y₂ являются подмножествами Y: для двух регионов, где функция не является инъективной, потому что более одного домена элемент может отображаться в один элемент диапазона. То есть возможно больше одного Икс в Икс сопоставить с такой же у в Y.

Делаем функции инъективными. Предыдущая функция ж : Икс → Y можно свести к одной или нескольким инъективным функциям (скажем) ж : Икс₁ → Y₁ и ж : Икс₂ → Y₂, показаны сплошными кривыми (части исходной кривой с длинными штрихами больше не отображаются). Обратите внимание, как правило ж не изменилось - только домен и диапазон. Икс₁ и Икс₂ являются подмножествами Икс, Y₁ и Y₂ являются подмножествами Y: для двух регионов, где начальная функция может быть сделана инъективной, чтобы один элемент домена мог отображаться в один элемент диапазона. То есть только один Икс в Икс соответствует одному у в Y.

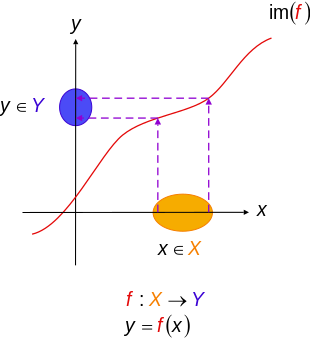
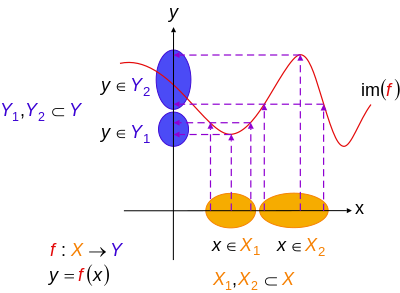
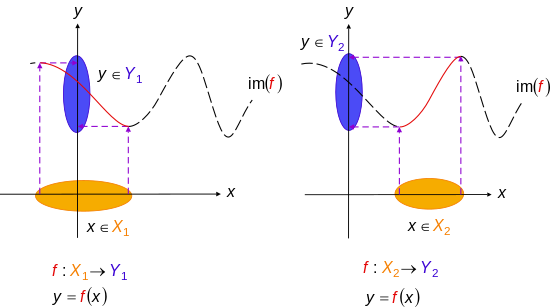
Инъекции можно отменить

Функции с левый обратный всегда уколы. То есть, учитывая ж : Икс → Y, если есть функция г : Y → Икс так что для каждого Икс ∈ Икс,

г(ж(Икс)) = Икс (ж может быть отменено г), тогда ж инъективно. В таком случае, г называется втягивание из ж. Наоборот, ж называется раздел из г.

И наоборот, каждая инъекция ж с непустым доменом имеет левую обратную г, который можно определить, закрепив элемент а в области ж так что г(Икс) равняется единственному прообразу Икс под ж если он существует и г(Икс) = а в противном случае.^[6]

Левая обратная г не обязательно обратный из ж, потому что композиция в другом порядке, ж ∘ г, может отличаться от идентичности на Y. Другими словами, инъективная функция может быть "обращена" левой обратной, но не обязательно обратимый, что требует, чтобы функция была биективный.

Инъекции могут быть обратимыми

Фактически, чтобы превратить инъективную функцию ж : Икс → Y в биективный (следовательно обратимый ), достаточно заменить ее домен Y по его фактическому диапазону J = ж(Икс). То есть пусть г : Икс → J такой, что г(Икс) = ж(Икс) для всех Икс в Икс; тогда г биективен. Действительно, ж можно разложить на множители как вкл._J,Y ∘ г, где вкл._J,Y это функция включения от J в Y.

В более общем смысле, инъективный частичные функции называются частичные отклонения.

Другие свойства

• Если ж и г оба инъективны, то ж ∘ г инъективно.

Композиция двух инъективных функций инъективна.

• Если г ∘ ж инъективно, то ж инъективно (но г не должно быть).
• ж : Икс → Y инъективен тогда и только тогда, когда для любых функций г, час : W → Икс всякий раз, когда ж ∘ г = ж ∘ час, тогда г = час. Другими словами, инъективные функции - это в точности мономорфизмы в категория Набор наборов.
• Если ж : Икс → Y инъективен и А это подмножество из Икс, тогда ж ⁻¹(ж(А)) = А. Таким образом, А можно восстановить из образ ж(А).
• Если ж : Икс → Y инъективен и А и B оба подмножества Икс, тогда ж(А ∩ B) = ж(А) ∩ ж(B).
• Каждая функция час : W → Y можно разложить как час = ж ∘ г для подходящей инъекции ж и сюрприз г. Это разложение уникально с точностью до изоморфизма, и ж можно рассматривать как функция включения диапазона час(W) из час как подмножество кодомена Y из час.
• Если ж : Икс → Y - инъективная функция, то Y имеет как минимум столько же элементов, сколько Икс, в том смысле Количественные числительные. В частности, если дополнительно идет укол от Y к Икс, тогда Икс и Y имеют одинаковый кардинальный номер. (Это известно как Теорема Кантора – Бернштейна – Шредера..)
• Если оба Икс и Y находятся конечный с таким же количеством элементов, то ж : Икс → Y инъективен тогда и только тогда, когда ж является сюръективный (в таком случае ж является биективный ).
• Инъективная функция, которая является гомоморфизм между двумя алгебраическими структурами есть встраивание.
• В отличие от сюръективности, которая представляет собой отношение между графиком функции и ее областью, инъективность является свойством только графика функции; то есть, будет ли функция ж инъективность может быть определена только при рассмотрении графа (а не домена) ж.

Доказательство инъективности функций

Доказательство того, что функция ж является инъективным, зависит от того, как функция представлена ​​и какие свойства имеет функция. Для функций, которые задаются некоторой формулой, есть основная идея. Мы используем определение инъективности, а именно, что если ж(Икс) = ж(у), тогда Икс = у.^[7]

Вот пример:

ж = 2Икс + 3

Доказательство: Пусть ж : Икс → Y. Предположим ж(Икс) = ж(у). Так 2Икс + 3 = 2у + 3 ⇒ 2Икс = 2у ⇒ Икс = у. Следовательно, из определения следует, что ж инъективно.

Есть несколько других методов доказательства инъективности функции. Например, в исчислении, если ж является дифференцируемой функцией, определенной на некотором интервале, то достаточно показать, что производная всегда положительна или всегда отрицательна на этом интервале. В линейной алгебре, если ж является линейным преобразованием, достаточно показать, что ядро ж содержит только нулевой вектор. Если ж является функцией с конечным доменом, достаточно просмотреть список изображений каждого элемента домена и убедиться, что ни одно изображение не встречается дважды в списке.

Графический подход к действительнозначной функции ж реальной переменной Икс это проверка горизонтальной линии. Если каждая горизонтальная линия пересекает кривую f (x) максимум в одной точке, затем ж является инъективным или однозначным.

Смотрите также

• Биекция, инъекция и сюръекция
• Инъективное метрическое пространство
• Монотонная функция
• Однолистная функция

Заметки

использованная литература

• Бартл, Роберт Г. (1976), Элементы реального анализа (2-е изд.), Нью-Йорк: Джон Уайли и сыновья, ISBN  978-0-471-05464-1, п. 17 ff.
• Халмос, Пол Р. (1974), Наивная теория множеств, Нью-Йорк: Springer, ISBN  978-0-387-90092-6, п. 38 ff.

внешние ссылки

• Самые ранние примеры использования некоторых слов математики: статья о инъекции, сюръекции и взаимно-взаимной инъекции имеет историю инъекции и связанных с ней терминов.
• Khan Academy - Сюръективные (на) и Инъективные (взаимно однозначные) функции: Введение в сюръективные и инъективные функции