Гомоморфизм - Википедия - Homomorphism

В алгебра, а гомоморфизм это структуросохраняющий карта между двумя алгебраические структуры одного типа (например, два группы, два кольца, или два векторные пространства ). Слово гомоморфизм исходит из древнегреческий язык: ὁμός (гомики) означает "такой же" и μορφή (морфе) что означает «форма» или «форма». Однако это слово, по-видимому, было введено в математику из-за (неправильного) перевода немецкого языка ähnlich что означает "похожий" на ὁμός что означает «такой же».^[1] Термин «гомоморфизм» появился еще в 1892 году, когда его приписали немецкому математику. Феликс Кляйн (1849–1925).^[2]

Гомоморфизмы векторных пространств также называют линейные карты, и их изучение является предметом линейная алгебра.

Понятие гомоморфизма было обобщено под названием морфизм, ко многим другим структурам, которые либо не имеют базового набора, либо не являются алгебраическими. Это обобщение является отправной точкой теория категорий.

Гомоморфизм также может быть изоморфизм, эндоморфизм, автоморфизм и т. д. (см. ниже). Каждый из них может быть определен способом, который может быть обобщен на любой класс морфизмов.

Определение

Гомоморфизм - это отображение между двумя алгебраические структуры того же типа (то есть с тем же именем), что сохраняет операции конструкций. Это означает карта ${ displaystyle f: от A до B}$ между двумя наборы ${ displaystyle A}$ , ${ displaystyle B}$ оборудован такой же конструкцией, что, если ${ displaystyle cdot}$ является операцией конструкции (здесь для упрощения предполагается бинарная операция ), тогда

{ Displaystyle е (х cdot y) = е (х) cdot f (y)}

для каждой пары ${ displaystyle x}$ , ${ displaystyle y}$ элементов ${ displaystyle A}$ .^{[примечание 1]} Часто говорят, что ${ displaystyle f}$ сохраняет операцию или совместим с ней.

Формально карта ${ displaystyle f: от A до B}$ сохраняет операцию ${ displaystyle mu}$ из арность k, определенные на обоих ${ displaystyle A}$ и ${ displaystyle B}$ если

{ displaystyle f ( mu _ {A} (a_ {1}, ldots, a_ {k})) = mu _ {B} (f (a_ {1}), ldots, f (a_ {k })),}

для всех элементов ${ displaystyle a_ {1}, ..., a_ {k}}$ в ${ displaystyle A}$ .

Операции, которые должны быть сохранены гомоморфизмом, включают 0-арные операции, то есть константы. В частности, когда элемент идентичности требуется типом структуры, элемент идентичности первой структуры должен быть отображен в соответствующий элемент идентичности второй структуры.

Например:

А гомоморфизм полугрупп это карта между полугруппы что сохраняет полугрупповую операцию.
А моноидный гомоморфизм это карта между моноиды который сохраняет операцию моноида и отображает единичный элемент первого моноида на единичный элемент второго моноида (единичный элемент является 0-арная операция ).
А групповой гомоморфизм это карта между группы что сохраняет групповую операцию. Отсюда следует, что гомоморфизм группы отображает единичный элемент первой группы в единичный элемент второй группы и отображает обратный элемента первой группы на инверсию изображения этого элемента. Таким образом, гомоморфизм полугрупп между группами обязательно является гомоморфизмом групп.
А кольцевой гомоморфизм это карта между кольца который сохраняет сложение колец, умножение колец и мультипликативная идентичность. Будет ли сохранена мультипликативная идентичность, зависит от определения звенеть в использовании. Если мультипликативное тождество не сохраняется, есть rng гомоморфизм.
А линейная карта является гомоморфизмом векторное пространство, Это групповой гомоморфизм векторных пространств, сохраняющий структуру абелевой группы и скалярное умножение.
А модульный гомоморфизм, также называемая линейной картой между модули, определяется аналогично.
An гомоморфизм алгебр карта, сохраняющая алгебра операции.

Алгебраическая структура может иметь более одной операции, и для сохранения каждой операции требуется гомоморфизм. Таким образом, отображение, сохраняющее только некоторые операции, не является гомоморфизмом структуры, а только гомоморфизмом подструктуры, полученной рассмотрением только сохраненных операций. Например, отображение между моноидами, которое сохраняет операцию моноида, а не единичный элемент, не является гомоморфизмом моноида, а только гомоморфизмом полугруппы.

Обозначения для операций не обязательно должны быть одинаковыми в источнике и цели гомоморфизма. Например, действительные числа образуют группу для сложения, а положительные действительные числа образуют группу для умножения. В экспоненциальная функция

{ Displaystyle х mapsto е ^ {х}}

удовлетворяет

{ Displaystyle е ^ {х + у} = е ^ {х} е ^ {у},}

и, таким образом, является гомоморфизмом между этими двумя группами. Это даже изоморфизм (см. Ниже), поскольку его обратная функция, то натуральный логарифм, удовлетворяет

{ Displaystyle пер (ху) = пер (х) + пер (у),}

и также является гомоморфизмом групп.

Примеры

Моноид гомоморфизм

{ displaystyle f}

из моноида

(N, +, 0)

к моноиду

(N, \times, 1)

, определяется

{ Displaystyle е (х) = 2 ^ {х}}

. это инъективный, но нет сюръективный.

В действительные числа площадь звенеть, имеющий как сложение, так и умножение. Набор всех 2 × 2 матрицы тоже кольцо, под матрица сложения и матричное умножение. Если мы определим функцию между этими кольцами следующим образом:

{ displaystyle f (r) = { begin {pmatrix} r & 0 0 & r end {pmatrix}}}

куда $р$ это действительное число, тогда $ж$ является гомоморфизмом колец, так как $ж$ сохраняет оба дополнения:

{ displaystyle f (r + s) = { begin {pmatrix} r + s & 0 0 & r + s end {pmatrix}} = { begin {pmatrix} r & 0 0 & r end {pmatrix}} + { begin {pmatrix} s & 0 0 & s end {pmatrix}} = f (r) + f (s)}

и умножение:

{ displaystyle f (rs) = { begin {pmatrix} rs & 0 0 & rs end {pmatrix}} = { begin {pmatrix} r & 0 0 & r end {pmatrix}} { begin {pmatrix} s & 0 0 & s end {pmatrix}} = f (r) , f (s).}

В другом примере ненулевое сложные числа сформировать группа при операции умножения, как и ненулевые действительные числа. (Ноль должен быть исключен из обеих групп, поскольку у него нет мультипликативный обратный, что требуется для элементов группы.) Определите функцию ${ displaystyle f}$ от ненулевых комплексных чисел к ненулевым действительным числам на

{ Displaystyle f (z) = | z |.}

То есть, ${ displaystyle f}$ это абсолютная величина (или модуль) комплексного числа ${ displaystyle z}$ . потом ${ displaystyle f}$ является гомоморфизмом групп, поскольку сохраняет умножение:

{ displaystyle f (z_ {1} z_ {2}) = | z_ {1} z_ {2} | = | z_ {1} || z_ {2} | = f (z_ {1}) f (z_ { 2}).}

Обратите внимание, что $ж$ не может быть продолжен до гомоморфизма колец (от комплексных чисел к действительным числам), так как он не сохраняет сложение:

{ displaystyle | z_ {1} + z_ {2} | neq | z_ {1} | + | z_ {2} |.}

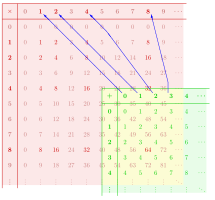
В качестве другого примера на диаграмме показан моноид гомоморфизм ${ displaystyle f}$ из моноида ${ displaystyle ( mathbb {N}, +, 0)}$ к моноиду ${ Displaystyle ( mathbb {N}, раз, 1)}$ . Из-за разных названий соответствующих операций свойства сохранения структуры удовлетворяют ${ displaystyle f}$ равняться ${ Displaystyle е (х + у) = е (х) раз е (у)}$ и ${ displaystyle f (0) = 1}$ .

А композиционная алгебра ${ displaystyle A}$ над полем ${ displaystyle F}$ имеет квадратичная форма, называется норма, ${ Displaystyle N: от A до F}$ , который является гомоморфизмом групп из мультипликативная группа из ${ displaystyle A}$ в мультипликативную группу ${ displaystyle F}$ .

Специальные гомоморфизмы

Некоторые виды гомоморфизмов имеют конкретное имя, которое также определено для общих морфизмы.

Изоморфизм

An изоморфизм между алгебраические структуры того же типа обычно определяется как биективный гомоморфизм.^[3]^:134 ^[4]^:28

В более общем контексте теория категорий, изоморфизм определяется как морфизм, который имеет обратный это тоже морфизм. В конкретном случае алгебраических структур эти два определения эквивалентны, хотя они могут отличаться для неалгебраических структур, которые имеют базовый набор.

Точнее, если

{ displaystyle f: от A до B}

является (гомо) морфизмом, он имеет обратный, если существует гомоморфизм

{ displaystyle g: B to A}

такой, что

{ displaystyle f circ g = operatorname {Id} _ {B} qquad { text {and}} qquad g circ f = operatorname {Id} _ {A}.}

Если ${ displaystyle A}$ и ${ displaystyle B}$ имеют базовые наборы, и ${ displaystyle f: от A до B}$ имеет обратный ${ displaystyle g}$ , тогда ${ displaystyle f}$ биективен. Фактически, ${ displaystyle f}$ является инъективный, так как ${ Displaystyle е (х) = е (у)}$ подразумевает ${ Displaystyle х = г (е (х)) = г (е (у)) = у}$ , и ${ displaystyle f}$ является сюръективный, как и для любого ${ displaystyle x}$ в ${ displaystyle B}$ , надо ${ Displaystyle х = е (г (х))}$ , и ${ displaystyle x}$ это изображение элемента ${ displaystyle A}$ .

Наоборот, если ${ displaystyle f: от A до B}$ является биективным гомоморфизмом между алгебраическими структурами, пусть ${ displaystyle g: B to A}$ быть такой картой, что ${ displaystyle g (y)}$ уникальный элемент ${ displaystyle x}$ из ${ displaystyle A}$ такой, что ${ Displaystyle е (х) = у}$ . Надо ${ displaystyle f circ g = operatorname {Id} _ {B} { text {and}} g circ f = operatorname {Id} _ {A},}$ и остается только показать, что $грамм$ является гомоморфизмом. Если ${ displaystyle *}$ является бинарной операцией структуры для каждой пары ${ displaystyle x}$ , ${ displaystyle y}$ элементов ${ displaystyle B}$ , надо

{ displaystyle g (x * _ {B} y) = g (f (g (x)) * _ {B} f (g (y))) = g (f (g (x) * _ {A}) g (y))) = g (x) * _ {A} g (y),}

и ${ displaystyle g}$ таким образом совместим с ${ displaystyle *.}$ Поскольку доказательство аналогично для любого арность, это показывает, что ${ displaystyle g}$ является гомоморфизмом.

Это доказательство не работает для неалгебраических структур. Например, для топологические пространства, морфизм - это непрерывная карта, и обратное к биективному непрерывному отображению не обязательно непрерывно. Изоморфизм топологических пространств, называемый гомеоморфизм или же двухсторонняя карта, таким образом, является биективным непрерывным отображением, обратное к которому также непрерывно.

Эндоморфизм

An эндоморфизм является гомоморфизмом, домен равно codomain, или, в более общем смысле, морфизм чей источник равен цели.^[3]^:135

Эндоморфизмы алгебраической структуры или объекта категория сформировать моноид под состав.

Эндоморфизмы векторное пространство или из модуль сформировать звенеть. В случае векторного пространства или бесплатный модуль конечных измерение, выбор основа вызывает изоморфизм колец между кольцом эндоморфизмов и кольцом квадратные матрицы того же измерения.

Автоморфизм

An автоморфизм является эндоморфизмом, который также является изоморфизмом.^[3]^:135

Автоморфизмы алгебраической структуры или объекта категории образуют группа по составу, который называется группа автоморфизмов конструкции.

Многие группы, получившие название, являются группами автоморфизмов некоторой алгебраической структуры. Например, общая линейная группа ${ displaystyle operatorname {GL} _ {n} (k)}$ группа автоморфизмов векторное пространство измерения ${ displaystyle n}$ через поле ${ displaystyle k}$ .

Группы автоморфизмов поля были представлены Эварист Галуа для изучения корни из многочлены, и являются основой Теория Галуа.

Мономорфизм

Для алгебраических структур мономорфизмы обычно определяются как инъективный гомоморфизмы.^[3]^:134 ^[4]^:29

В более общем контексте теория категорий, мономорфизм определяется как морфизм то есть оставлено отменяемым.^[5] Это означает, что (гомо) морфизм ${ displaystyle f: от A до B}$ является мономорфизмом, если для любой пары ${ displaystyle g}$ , ${ displaystyle h}$ морфизмов из любого другого объекта ${ displaystyle C}$ к ${ displaystyle A}$ , тогда ${ displaystyle f circ g = f circ h}$ подразумевает ${ displaystyle g = h}$ .

Эти два определения мономорфизм эквивалентны для всех распространенных алгебраических структур. Точнее, они эквивалентны для поля, для которого каждый гомоморфизм является мономорфизмом, а для разновидности из универсальная алгебра, то есть алгебраические структуры, для которых операции и аксиомы (тождества) определены без каких-либо ограничений (поля не являются разнообразием, поскольку мультипликативный обратный определяется либо как унарная операция или как свойство умножения, которые в обоих случаях определены только для ненулевых элементов).

В частности, два определения мономорфизма эквивалентны для наборы, магмы, полугруппы, моноиды, группы, кольца, поля, векторные пространства и модули.

А расщепляемый мономорфизм является гомоморфизмом, имеющим левый обратный и, таким образом, он сам является прямым обратным этому другому гомоморфизму. То есть гомоморфизм ${ displaystyle f двоеточие от A до B}$ расщепляемый гомоморфизм, если существует гомоморфизм ${ displaystyle g двоеточие от B до A}$ такой, что ${ displaystyle g circ f = operatorname {Id} _ {A}.}$ Расщепляемый мономорфизм всегда является мономорфизмом для обоих значений мономорфизм. Для множеств и векторных пространств каждый мономорфизм является расщепляемым гомоморфизмом, но это свойство не выполняется для большинства общих алгебраических структур.

Доказательство эквивалентности двух определений мономорфизмов

Инъективный гомоморфизм сокращается слева: Если ${ displaystyle f circ g = f circ h,}$ надо ${ Displaystyle е (г (х)) = е (час (х))}$ для каждого ${ displaystyle x}$ в ${ displaystyle C}$ , общий источник ${ displaystyle g}$ и ${ displaystyle h}$ . Если ${ displaystyle f}$ инъективно, то ${ Displaystyle г (х) = час (х)}$ , и поэтому ${ displaystyle g = h}$ . Это доказательство работает не только для алгебраических структур, но и для любых категория объекты которых являются наборами, а стрелки - отображениями между этими наборами. Например, инъективное непрерывное отображение - это мономорфизм в категории топологические пространства.

Для доказательства того, что, наоборот, сокращаемый слева гомоморфизм инъективен, полезно рассмотреть свободный объект на ${ displaystyle x}$ . Учитывая разнообразие алгебраических структур свободный объект на ${ displaystyle x}$ пара, состоящая из алгебраической структуры ${ displaystyle L}$ этого разнообразия и элемента ${ displaystyle x}$ из ${ displaystyle L}$ удовлетворяющий следующим универсальная собственность: для каждой конструкции ${ displaystyle S}$ разнообразия, и каждый элемент ${ displaystyle s}$ из ${ displaystyle S}$ , существует единственный гомоморфизм ${ displaystyle f: L to S}$ такой, что ${ displaystyle f (x) = s}$ . Например, для наборов бесплатный объект на ${ displaystyle x}$ просто ${ Displaystyle {х }}$ ; за полугруппы, бесплатный объект на ${ displaystyle x}$ является ${ Displaystyle {х, х ^ {2}, ldots, х ^ {п}, ldots },}$ которая как полугруппа изоморфна аддитивной полугруппе натуральных чисел; за моноиды, бесплатный объект на ${ displaystyle x}$ является ${ displaystyle {1, x, x ^ {2}, ldots, x ^ {n}, ldots },}$ который, как моноид, изоморфен аддитивному моноиду неотрицательных целых чисел; за группы, бесплатный объект на ${ displaystyle x}$ это бесконечная циклическая группа ${ Displaystyle { ldots, x ^ {- n}, ldots, x ^ {- 1}, 1, x, x ^ {2}, ldots, x ^ {n}, ldots },}$ которая, как группа, изоморфна аддитивной группе целых чисел; за кольца, бесплатный объект на ${ displaystyle x}$ } это кольцо многочленов ${ Displaystyle mathbb {Z} [х];}$ за векторные пространства или же модули, бесплатный объект на ${ displaystyle x}$ это векторное пространство или свободный модуль, имеющий ${ displaystyle x}$ как основу.

Если свободный объект закончился ${ displaystyle x}$ существует, то каждый сокращаемый слева гомоморфизм инъективен: позволять ${ displaystyle f двоеточие от A до B}$ - сократимый слева гомоморфизм, и ${ displaystyle a}$ и ${ displaystyle b}$ быть двумя элементами ${ displaystyle A}$ такой ${ Displaystyle е (а) = е (Ь)}$ . По определению бесплатного объекта ${ displaystyle F}$ , существуют гомоморфизмы ${ displaystyle g}$ и ${ displaystyle h}$ из ${ displaystyle F}$ к ${ displaystyle A}$ такой, что ${ Displaystyle г (х) = а}$ и ${ Displaystyle ч (х) = Ь}$ . В качестве ${ Displaystyle е (г (х)) = е (час (х))}$ , надо ${ Displaystyle f circ g = f circ h,}$ по единственности определения универсального свойства. В качестве ${ displaystyle f}$ остается отменяемым, есть ${ displaystyle g = h}$ , и поэтому ${ displaystyle a = b}$ . Следовательно, ${ displaystyle f}$ инъективно.

Наличие бесплатного объекта на ${ displaystyle x}$ для разнообразие (смотрите также Свободный объект § Существование ): Для построения свободного объекта поверх ${ displaystyle x}$ , рассмотрим множество ${ displaystyle W}$ из правильные формулы построен из ${ displaystyle x}$ и операции структуры. Две такие формулы называются эквивалентными, если можно перейти от одной к другой, применяя аксиомы (идентичности конструкции). Это определяет отношение эквивалентности, если идентичности не подчиняются условиям, то есть если работаете с разнообразием. Тогда операции многообразия корректно определены на множестве классы эквивалентности из ${ displaystyle W}$ для этого отношения. Несложно показать, что получившийся объект является свободным объектом на ${ displaystyle W}$ .

Эпиморфизм

В алгебра, эпиморфизмы часто определяются как сюръективный гомоморфизмы.^[3]^:134^[4]^:43 С другой стороны, в теория категорий, эпиморфизмы определены как право отменяемое морфизмы.^[5] Это означает, что (гомо) морфизм ${ displaystyle f: от A до B}$ является эпиморфизмом, если для любой пары ${ displaystyle g}$ , ${ displaystyle h}$ морфизмов из ${ displaystyle B}$ к любому другому объекту ${ displaystyle C}$ , равенство ${ Displaystyle г CIRC F = H CIRC F}$ подразумевает ${ displaystyle g = h}$ .

Сюръективный гомоморфизм всегда сокращается справа, но обратное не всегда верно для алгебраических структур. Однако два определения эпиморфизм эквивалентны для наборы, векторные пространства, абелевы группы, модули (см. доказательство ниже), и группы.^[6] Важность этих структур во всей математике и особенно в линейная алгебра и гомологическая алгебра, может объяснить сосуществование двух неэквивалентных определений.

Алгебраические структуры, для которых существуют несюръективные эпиморфизмы, включают полугруппы и кольца. Самый простой пример - включение целые числа в рациональное число, который является гомоморфизмом колец и мультипликативных полугрупп. Для обеих структур это мономорфизм и несюръективный эпиморфизм, но не изоморфизм.^[5]^[7]

Широкое обобщение этого примера - локализация кольца мультипликативным множеством. Каждая локализация - это кольцевой эпиморфизм, который, вообще говоря, не сюръективен. Поскольку локализация является фундаментальной в коммутативная алгебра и алгебраическая геометрия, это может объяснить, почему в этих областях определение эпиморфизмов как сокращаемых справа гомоморфизмов обычно является предпочтительным.

А расщепленный эпиморфизм является гомоморфизмом, имеющим правый обратный и поэтому он сам является левым обратным к этому другому гомоморфизму. То есть гомоморфизм ${ displaystyle f двоеточие от A до B}$ является расщепляемым эпиморфизмом, если существует гомоморфизм ${ displaystyle g двоеточие от B до A}$ такой, что ${ displaystyle f circ g = operatorname {Id} _ {B}.}$ Расщепленный эпиморфизм всегда является эпиморфизмом для обоих значений эпиморфизм. Для множеств и векторных пространств каждый эпиморфизм является расщепляемым эпиморфизмом, но это свойство не выполняется для большинства общих алгебраических структур.

Таким образом, есть

{ displaystyle { text {разделенный эпиморфизм}} подразумевает { text {эпиморфизм (сюръективный)}} подразумевает { text {эпиморфизм (правый отменяемый)}};}

последняя импликация - эквивалентность множеств, векторных пространств, модулей и абелевых групп; первая импликация - это эквивалентность множеств и векторных пространств.

Эквивалентность двух определений эпиморфизма

Позволять ${ displaystyle f двоеточие от A до B}$ - гомоморфизм. Мы хотим доказать, что если оно не сюръективно, оно не может быть сокращено.

В случае множеств пусть ${ displaystyle b}$ быть элементом ${ displaystyle B}$ это не принадлежит ${ displaystyle f (A)}$ , и определим ${ displaystyle g, h двоеточие от B до B}$ такой, что ${ displaystyle g}$ это функция идентичности, и это ${ Displaystyle ч (х) = х}$ для каждого ${ displaystyle x in B,}$ Кроме этого ${ displaystyle h (b)}$ любой другой элемент ${ displaystyle B}$ . Четко ${ displaystyle f}$ не может быть отменен, так как ${ displaystyle g neq h}$ и ${ displaystyle g circ f = h circ f.}$

В случае векторных пространств, абелевых групп и модулей доказательство опирается на существование коядра и о том, что нулевые карты являются гомоморфизмами: пусть ${ displaystyle C}$ быть ядром ${ displaystyle f}$ , и ${ displaystyle g двоеточие от B до C}$ - каноническое отображение, такое что ${ Displaystyle г (е (А)) = 0}$ . Позволять ${ displaystyle h двоеточие B to C}$ - нулевая карта. Если ${ displaystyle f}$ не сюръективно, ${ displaystyle C neq 0}$ , и поэтому ${ displaystyle g neq h}$ (одна - нулевая карта, а другая - нет). Таким образом ${ displaystyle f}$ не отменяется, так как ${ Displaystyle г CIRC F = H CIRC F}$ (оба являются нулевой картой из ${ displaystyle A}$ к ${ displaystyle C}$ ).

Ядро

Любой гомоморфизм ${ displaystyle f: от X до Y}$ определяет отношение эквивалентности ${ displaystyle sim}$ на ${ displaystyle X}$ к ${ displaystyle a sim b}$ если и только если ${ Displaystyle е (а) = е (Ь)}$ . Соотношение ${ displaystyle sim}$ называется ядро из ${ displaystyle f}$ . Это отношение конгруэнтности на ${ displaystyle X}$ . В набор частных ${ displaystyle X / { sim}}$ затем можно задать структуру того же типа, что и ${ displaystyle X}$ , естественным образом, определяя операции частного множества ${ Displaystyle [х] аст [у] = [х аст у]}$ , для каждой операции ${ displaystyle ast}$ из ${ displaystyle X}$ . В этом случае изображение ${ displaystyle X}$ в ${ displaystyle Y}$ при гомоморфизме ${ displaystyle f}$ обязательно изоморфный к ${ Displaystyle X / ! sim}$ ; этот факт является одним из теоремы об изоморфизме.

Когда алгебраическая структура является группа для какой-то операции класс эквивалентности ${ displaystyle K}$ из элемент идентичности этой операции достаточно, чтобы охарактеризовать отношение эквивалентности. В этом случае фактор по отношению эквивалентности обозначается через ${ Displaystyle X / K}$ (обычно читается как " ${ displaystyle X}$ мод ${ displaystyle K}$ "). Также в этом случае это ${ displaystyle K}$ , скорее, чем ${ displaystyle sim}$ , что называется ядро из ${ displaystyle f}$ . Ядра гомоморфизмов данного типа алгебраической структуры естественным образом снабжены некоторой структурой. Этот структурный тип ядер совпадает с рассмотренной структурой в случае абелевы группы, векторные пространства и модули, но отличается и в других случаях получает конкретное имя, например нормальная подгруппа для ядер гомоморфизмы групп и идеалы для ядер гомоморфизмы колец (в случае некоммутативных колец ядрами являются двусторонние идеалы ).

Реляционные структуры

В теория моделей, понятие алгебраической структуры обобщается на структуры, включающие как операции, так и отношения. Позволять L - подпись, состоящая из символов функций и отношений, и А, B быть двумя L-конструкции. Затем гомоморфизм из А к B это отображение час из области А в область B такой, что

час(F^А(а₁,…,а_п)) = F^B(час(а₁),…,час(а_п)) для каждого псимвол функции F в L,
р^А(а₁,…,а_п) подразумевает р^B(час(а₁),…,час(а_п)) для каждого псимвол -арное отношение р в L.

В частном случае всего с одним бинарным отношением мы получаем понятие гомоморфизм графов. Для подробного обсуждения реляционных гомоморфизмов и изоморфизмов см.^[8]

Теория формального языка

Гомоморфизмы также используются при изучении формальные языки^[9] и часто кратко называют морфизмами.^[10] Данные алфавиты Σ₁ и Σ₂, функция час : Σ₁^∗ → Σ₂^∗ такой, что час(УФ) = час(ты) час(v) для всех ты и v в Σ₁^∗ называется гомоморфизм на Σ₁^∗.^{[заметка 2]} Если час является гомоморфизмом на Σ₁^∗ и е обозначает пустое слово, то час называется е-свободный гомоморфизм когда час(Икс) ≠ е для всех Икс ≠ е в Σ₁^∗.

Множество Σ^∗ слов, образованных из алфавита Σ, можно рассматривать как свободный моноид порожденный Σ. Здесь моноидная операция - это конкатенация, а элементом идентичности является пустое слово. С этой точки зрения гомоморфизм языка - это в точности гомоморфизм моноида.^{[заметка 3]}

Смотрите также

Непрерывная функция
Диффеоморфизм
Гомоморфное шифрование
Гомоморфное разделение секретов - упрощенный децентрализованный протокол голосования
Морфизм

Примечания

^ Как это часто бывает, но не всегда, один и тот же символ для работы обоих ${ displaystyle A}$ и ${ displaystyle B}$ здесь использовался.
^ Символ * обозначает Клини звезда операции, а Σ^∗ обозначает множество слов, образованных из алфавита Σ, включая пустое слово. Сопоставление терминов означает конкатенация. Например, час(ты) час(v) обозначает конкатенацию час(ты) с час(v).
^ Мы уверены, что гомоморфизм языков час отображает пустое слово е к пустому слову. С час(е) = час(ее) = час(е)час(е), номер ш персонажей в час(е) равно числу 2ш персонажей в час(е)час(е). Следовательно ш = 0 и час(е) имеет нулевую длину.

Цитаты

^ Фрике, Роберт (1897–1912). Vorlesungen über die Theorie der automorphen Functionen. Б.Г. Teubner. OCLC 29857037.
^
Видеть:
- Риттер, Эрнст (1892). "Die eindeutigen automorphen Formen vom Geschlecht Null, eine Revision und Erweiterung der Poincaré'schen Sätze" [Уникальные автоморфные формы рода нуль, пересмотр и расширение теоремы Пуанкаре]. Mathematische Annalen (на немецком). 41: 1–82. Дои:10.1007 / BF01443449. S2CID 121524108. Из сноски на стр. 22: "Ich will nach einem Vorschlage von Hrn. Prof. Klein statt der umständlichen und nicht immer ausreichenden Bezeichnungen:" holoedrisch, bezw. hemiedrisch u.s.w. isomorph "die Benennung" isomorph "auf den Fall des Holoedrischen Isomorphismus zweier Gruppen einschränken, sonst aber von "Homomorphismus" sprechen,… " (Следуя предложению профессора Кляйна, вместо громоздких и не всегда удовлетворительных обозначений «голоэдрический, или полуэдрический и т. Д. Изоморфный» я ограничу наименование «изоморфный» случаем голоэдрический изоморфизм двух групп; в противном случае, однако, [я] буду говорить о «гомоморфизме»,…)
- Фрике, Роберт (1892). "Ueber den arithmetischen Charakter der zu den Verzweigungen (2,3,7) und (2,4,7) gehörenden Dreiecksfunctionen" [Об арифметическом характере функций треугольника, принадлежащих точкам ветвления (2,3,7) и (2,4,7)]. Mathematische Annalen (на немецком). 41: 443–468. Дои:10.1007 / BF01443421. S2CID 120022176. С п. 466: "Hierdurch ist, wie man sofort überblickt, eine homomorphe *) Beziehung der Gruppe Γ₍₆₃₎ auf die Gruppe der mod. n incongruenten Substitutionen mit rationalen ganzen Coefficienten der Determinante 1 begin. " (Таким образом, как сразу видно, гомоморфное отношение группы Γ₍₆₃₎ основан на группе инконгруэнтных подстановок по модулю n с целыми рациональными коэффициентами определителя 1.) Из сноски на стр. 466: "*) Im Anschluss an einen von Hrn. Klein bei seinen neueren Vorlesungen eingeführten Brauch schreibe ich an Stelle der bisherigen Bezeichnung" meroedrischer Isomorphismus "die sinngemässere" Homomorphism ". (Следуя использованию, которое было введено г-ном Кляйном во время его недавних лекций, я пишу вместо прежнего обозначения «мероэдрический изоморфизм» более логичный «гомоморфизм».)
^ ^а ^б ^c ^d ^е Биркгоф, Гарретт (1967) [1940], Теория решетки, Публикации коллоквиума Американского математического общества, 25 (3-е изд.), Providence, R.I .: Американское математическое общество, ISBN 978-0-8218-1025-5, МИСТЕР 0598630
^ ^а ^б ^c Стэнли Н. Беррис; H.P. Санкаппанавар (2012). Курс универсальной алгебры (PDF). ISBN 978-0-9880552-0-9.
^ ^а ^б ^c Мак-Лейн, Сондерс (1971). Категории для рабочего математика. Тексты для выпускников по математике. 5. Springer-Verlag. Упражнение 4 из раздела I.5. ISBN 0-387-90036-5. Zbl 0232.18001.
^ Линдерхольм, К. Э. (1970). Групповой эпиморфизм сюръективен. Американский математический ежемесячник, 77(2), 176-177.
^ Дэскэлеску, Сорин; Нэстэсеску, Константин; Райану, Щербан (2001). Алгебра Хопфа: Введение. Чистая и прикладная математика. 235. Нью-Йорк, Нью-Йорк: Марсель Деккер. п. 363. ISBN 0824704819. Zbl 0962.16026.
^ Раздел 17.4, в Гюнтер Шмидт, 2010. Реляционная математика. Издательство Кембриджского университета, ISBN 978-0-521-76268-7
^ Сеймур Гинзбург, Алгебраические и теоретико-автоматные свойства формальных языков, Северная Голландия, 1975 г., ISBN 0-7204-2506-9,
^ Т. Харью, Я. Кархумёки, Морфизмы в Справочник формальных языков, Том I, под редакцией Г. Розенберга, А. Саломаа, Springer, 1997 г., ISBN 3-540-61486-9.