Класс эквивалентности - Equivalence class

Конгруэнтность является примером отношения эквивалентности. Два крайних левых треугольника конгруэнтны, а третий и четвертый треугольники не конгруэнтны какому-либо другому показанному здесь треугольнику. Таким образом, первые два треугольника относятся к одному классу эквивалентности, а третий и четвертый треугольники находятся в своем собственном классе эквивалентности.

В математика, когда элементы некоторых набор $S$ имеют понятие эквивалентности (формализованное как отношение эквивалентности ), определенные на них, то можно естественным образом разбить множество $S$ в классы эквивалентности. Эти классы эквивалентности построены так, что элементы $а$ и $б$ принадлежат к тому же класс эквивалентности если и только если, они эквивалентны.

Формально с учетом набора $S$ и отношение эквивалентности $~$ на $S$ , то класс эквивалентности элемента $а$ в $S$ , обозначаемый ${displaystyle [a]}$ ,^[1]^[2] это набор^[3]

{displaystyle {xin Smid xsim a}}

элементов, которые эквивалентны $а$ . Из определяющих свойств отношений эквивалентности можно доказать, что классы эквивалентности образуют раздел из $S$ . Это разбиение - множество классов эквивалентности - иногда называют набор частных или факторное пространство из $S$ к $~$ , и обозначается $S / ~$ .

Когда набор $S$ имеет некоторую структуру (например, групповая операция или топология ) и отношение эквивалентности $~$ совместим с этой структурой, факторное множество часто наследует аналогичную структуру от своего родительского набора. Примеры включают факторпространства в линейной алгебре, факторпространства в топологии, факторгруппы, однородные пространства, кольца частных, частные моноиды, и факторные категории.

Примеры

Если $Икс$ это набор всех машин, а $~$ это отношение эквивалентности «имеет тот же цвет, что и», тогда один конкретный класс эквивалентности будет состоять из всех зеленых автомобилей, и $Икс /~$ естественным образом идентифицируется с набором всех цветов автомобилей.
Позволять $Икс$ - множество всех прямоугольников на плоскости, и $~$ отношение эквивалентности "имеет ту же площадь, что и", тогда для каждого положительного действительного числа А, будет класс эквивалентности всех прямоугольников, имеющих площадь А.^[4]
Рассмотрим по модулю 2 отношение эквивалентности на множестве целые числа, $ℤ$ , так что $Икс ~ у$ если и только если их разница $Икс - у$ является четное число. Это отношение порождает ровно два класса эквивалентности: один класс состоит из всех четных чисел, а другой класс состоит из всех нечетных чисел. Используя квадратные скобки вокруг одного члена класса для обозначения класса эквивалентности в этом отношении, $[7]$ , $[9]$ , и $[1]$ все представляют собой один и тот же элемент $ℤ / ~$ .^[5]
Позволять $Икс$ быть набором заказанные пары целых чисел $(а, б)$ с ненулевым $б$ , и определим отношение эквивалентности $~$ на $Икс$ такой, что $(а, б) ~ (c, d)$ если и только если $объявление = до н.э$ , то класс эквивалентности пары $(а, б)$ можно отождествить с Рациональное число $а / б$ , и это отношение эквивалентности и его классы эквивалентности могут использоваться для формального определения множества рациональных чисел.^[6] Эту же конструкцию можно обобщить на поле дробей любой область целостности.
Если $Икс$ состоит из всех строк, скажем, в Евклидова плоскость, и L ~ M Значит это L и M находятся параллельные линии, то набор параллельных друг другу прямых образует класс эквивалентности, пока линия считается параллельной самой себе. В этой ситуации каждый класс эквивалентности определяет точка в бесконечности.

Обозначения и формальное определение

An отношение эквивалентности на съемочной площадке $Икс$ это бинарное отношение $~$ на $Икс$ удовлетворяющий трем свойствам:^[7]^[8]

$а ~ а$ для всех $а$ в $Икс$ (рефлексивность ),
$а ~ б$ подразумевает $б ~ а$ для всех $а$ и $б$ в $Икс$ (симметрия ),
если $а ~ б$ и $б ~ c$ тогда $а ~ c$ для всех $а$ , $б$ , и $c$ в $Икс$ (транзитивность ).

Класс эквивалентности элемента $а$ обозначается $[а]$ или же $[а] ~$ ,^[1] и определяется как множество ${displaystyle {xin Xmid asim x}}$ элементов, связанных с $а$ к $~$ .^[3] Слово «класс» в термине «класс эквивалентности» не относится к классы как определено в теория множеств, однако классы эквивалентности часто оказываются правильные классы.

Множество всех классов эквивалентности в $Икс$ относительно отношения эквивалентности $р$ обозначается как $Икс / р$ , и называется $Икс$ по модулю $р$ (или набор частных из $Икс$ к $р$ ).^[9] В сюръективная карта ${displaystyle xmapsto [x]}$ из $Икс$ на $Икс / р$ , который отображает каждый элемент в его класс эквивалентности, называется каноническая сюръекция, или каноническая проекционная карта.

Когда элемент выбирается (часто неявно) в каждом классе эквивалентности, это определяет инъективная карта называется раздел. Если этот участок обозначить $s$ , надо $[s (c)] = c$ для каждого класса эквивалентности $c$ . Элемент $s (c)$ называется представитель из $c$ . Любой элемент класса может быть выбран в качестве представителя класса, выбрав соответствующий раздел.

Иногда есть раздел, который более «естественен», чем другие. В этом случае представители называются канонический представители. Например, в модульная арифметика рассмотрим отношение эквивалентности целых чисел, определенное следующим образом: $а ~ б$ если $а - б$ кратно заданному положительному целому числу $п$ (называется модуль). Каждый класс содержит уникальное неотрицательное целое число меньше, чем $п$ , и эти целые числа являются каноническими представителями. Класс и его представитель более или менее идентифицированы, о чем свидетельствует тот факт, что обозначение $а мод п$ может обозначать либо класс, либо его канонического представителя (которым является остаток из разделение из $а$ к $п$ ).

Характеристики

Каждый элемент $Икс$ из $Икс$ является членом класса эквивалентности $[Икс]$ . Каждые два класса эквивалентности $[Икс]$ и $[у]$ либо равны, либо непересекающийся. Следовательно, множество всех классов эквивалентности $Икс$ образует раздел из $Икс$ : каждый элемент $Икс$ принадлежит к одному и только одному классу эквивалентности.^[10] И наоборот, каждый раздел $Икс$ происходит из отношения эквивалентности таким образом, согласно которому $Икс ~ у$ если и только если $Икс$ и $у$ принадлежат к одному набору раздела.^[11]

Из свойств отношения эквивалентности следует, что

Икс ~ у

если и только если

[Икс] = [у]

.

Другими словами, если $~$ является отношением эквивалентности на множестве $Икс$ , и $Икс$ и $у$ два элемента $Икс$ , то эти утверждения эквивалентны:

${displaystyle xsim y}$
${displaystyle [x] = [y]}$
${displaystyle [x] cap [y] eq emptyset.}$

Графическое представление

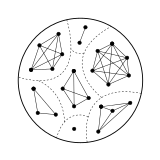
График примерной эквивалентности с 7 классами

An неориентированный граф может быть связан с любым симметричное отношение на съемочной площадке $Икс$ , где вершинами являются элементы $Икс$ , и две вершины $s$ и $т$ соединяются тогда и только тогда, когда $s ~ т$ . Среди этих графов есть графы отношений эквивалентности; они характеризуются как графики такие, что связанные компоненты находятся клики.^[12]

Инварианты

Если $~$ является отношением эквивалентности на $Икс$ , и $п (Икс)$ является свойством элементов $Икс$ так что всякий раз, когда $Икс ~ у$ , $п (Икс)$ верно, если $п (у)$ верно, то свойство $п$ считается инвариантный из $~$ , или же четко определенный по отношению $~$ .

Частый частный случай возникает, когда $ж$ это функция от $Икс$ в другой набор $Y$ ; если $ж (Икс 1) = ж (Икс 2)$ в любое время $Икс 1 ~ Икс 2$ , тогда $ж$ как говорят инвариант класса относительно $~$ , или просто инвариантен относительно $~$ . Это происходит, например, в теории характеров конечных групп. Некоторые авторы используют "совместимый с $~$ "или просто" уважает $~$ "вместо" инвариантен относительно $~$ ".

Любой функция $ж : Икс \to Y$ сам определяет отношение эквивалентности на $Икс$ в соответствии с которым $Икс 1 ~ Икс 2$ если и только если $ж (Икс 1) = ж (Икс 2)$ . Класс эквивалентности $Икс$ это набор всех элементов в $Икс$ которые сопоставляются с $ж (Икс)$ , т.е. класс $[Икс]$ это обратное изображение из $ж (Икс)$ . Это отношение эквивалентности известно как ядро из $ж$ .

В более общем плане функция может отображать эквивалентные аргументы (в соответствии с отношением эквивалентности $~ Икс$ на $Икс$ ) на эквивалентные значения (при условии эквивалентности $~ Y$ на $Y$ ). Такая функция является морфизм множеств, снабженных отношением эквивалентности.

Факторное пространство в топологии

В топология, а факторное пространство это топологическое пространство формируется на множестве классов эквивалентности отношения эквивалентности в топологическом пространстве, используя топологию исходного пространства для создания топологии на множестве классов эквивалентности.

В абстрактная алгебра, отношения конгруэнтности на базовом множестве алгебры позволяют алгебре индуцировать алгебру на классах эквивалентности отношения, называемую фактор-алгебра. В линейная алгебра, а факторное пространство векторное пространство, образованное взятием факторгруппа, где фактор-гомоморфизм линейная карта. В более широком смысле, в абстрактной алгебре термин фактор-пространство может использоваться для обозначения модули частных, кольца частных, факторгруппы, или любая фактор-алгебра. Однако использование этого термина для более общих случаев может проводиться по аналогии с орбитами группового действия.

Орбиты групповое действие на множестве может быть названо факторпространством действия на множестве, особенно когда орбиты группового действия являются правильными смежные классы подгруппы группы, которые возникают в результате действия подгруппы на группу левыми переводами, или, соответственно, левые смежные классы как орбиты при правом переносе.

Нормальная подгруппа топологической группы, действующая на группу действием сдвига, является фактор-пространством одновременно в смысле топологии, абстрактной алгебры и групповых действий.

Хотя этот термин может использоваться для любого набора классов эквивалентности отношения эквивалентности, возможно, с дополнительной структурой, цель использования термина, как правило, заключается в сравнении этого типа отношения эквивалентности на множестве. $Икс$ , либо к отношению эквивалентности, которое индуцирует некоторую структуру на множестве классов эквивалентности из структуры того же типа на $Икс$ , или к орбитам группового действия. И смысл структуры, сохраняемой отношением эквивалентности, и изучение инварианты под групповыми действиями приводят к определению инварианты приведенных выше отношений эквивалентности.

Смотрите также

Разделение эквивалентности, метод создания тестовых наборов в тестирование программного обеспечения основан на разделении возможных входов программы на классы эквивалентности в соответствии с поведением программы на этих входах
Однородное пространство, факторпространство Группы Ли
Отношение частичной эквивалентности
Фактор по отношению эквивалентности
Трансверсаль (комбинаторика)

Примечания

^ ^а ^б «Исчерпывающий список символов алгебры». Математическое хранилище. 2020-03-25. Получено 2020-08-30.
^ «7.3: Классы эквивалентности». Математика LibreTexts. 2017-09-20. Получено 2020-08-30.
^ ^а ^б Вайсштейн, Эрик В. «Класс эквивалентности». mathworld.wolfram.com. Получено 2020-08-30.
^ Авельсгаард 1989, п. 127
^ Девлин 2004, п. 123
^ Мэддокс 2002, стр. 77–78
^ Девлин 2004, п. 122
^ Вайсштейн, Эрик В. «Отношение эквивалентности». mathworld.wolfram.com. Получено 2020-08-30.
^ Волк 1998, п. 178
^ Мэддокс 2002, п. 74, Thm. 2.5.15
^ Авельсгаард 1989, п. 132, Thm. 3,16
^ Девлин 2004, п. 123

дальнейшее чтение

Сандстрем (2003), Математическое мышление: написание и доказательство, Прентис-Холл
Смит; Эгген; Святой Андрей (2006), Переход к высшей математике (6-е изд.), Томсон (Брукс / Коул)
Шумахер, Кэрол (1996), Глава нулевая: основные понятия абстрактной математики, Эддисон-Уэсли, ISBN 0-201-82653-4
О'Лири (2003), Структура доказательства: с помощью логики и теории множеств, Прентис-Холл
Lay (2001), Анализ с введением в доказательство, Прентис Холл
Мораш, Рональд П. (1987), Мост к абстрактной математике, Случайный дом, ISBN 0-394-35429-X
Гилберт; Ванстон (2005), Введение в математическое мышление, Пирсон Прентис-Холл
Флетчер; Пэтти, Основы высшей математики, PWS-Kent
Иглевич; Стойл, Введение в математические рассуждения, MacMillan
Д'Анджело; Запад (2000), Математическое мышление: решение проблем и доказательства, Прентис Холл
Купиллари, Гайки и болты доказательств, Уодсворт
Связь, Введение в абстрактную математику, Брукс / Коул
Барнье; Фельдман (2000), Введение в высшую математику, Прентис Холл
Пепел, Учебник по абстрактной математике, MAA

внешняя ссылка

СМИ, связанные с Классы эквивалентности в Wikimedia Commons

[:0-1] а ^б «Исчерпывающий список символов алгебры». Математическое хранилище. 2020-03-25. Получено 2020-08-30.

[2] «7.3: Классы эквивалентности». Математика LibreTexts. 2017-09-20. Получено 2020-08-30.

[:1-3] а ^б Вайсштейн, Эрик В. «Класс эквивалентности». mathworld.wolfram.com. Получено 2020-08-30.

[4] Авельсгаард 1989, п. 127

[5] Девлин 2004, п. 123

[6] Мэддокс 2002, стр. 77–78

[7] Девлин 2004, п. 122

[8] Вайсштейн, Эрик В. «Отношение эквивалентности». mathworld.wolfram.com. Получено 2020-08-30.

[9] Волк 1998, п. 178

[10] Мэддокс 2002, п. 74, Thm. 2.5.15

[11] Авельсгаард 1989, п. 132, Thm. 3,16

[12] Девлин 2004, п. 123

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]