Симметричное отношение - Symmetric relation

Бинарные отношения

	Симметричный	Антисимметричный	Connex	Обоснованный	Присоединяется	Встречается
Отношение эквивалентности	✓	✗	✗	✗	✗	✗
Предварительный заказ (Квазипорядок)	✗	✗	✗	✗	✗	✗
Частичный заказ	✗	✓	✗	✗	✗	✗
Всего предзаказ	✗	✗	✓	✗	✗	✗
Общий заказ	✗	✓	✓	✗	✗	✗
Предварительный заказ	✗	✗	✓	✓	✗	✗
Хорошо-квазиупорядоченный	✗	✗	✗	✓	✗	✗
Хороший порядок	✗	✓	✓	✓	✗	✗
Решетка	✗	✓	✗	✗	✓	✓
Соединение-полурешетка	✗	✓	✗	✗	✓	✗
Встреча-полурешетка	✗	✓	✗	✗	✗	✓

А "✓"означает, что свойство столбца требуется в определении строки.
Например, определение отношения эквивалентности требует, чтобы оно было симметричным.
Все определения молчаливо требуют транзитивность и рефлексивность.

А симметричное отношение это тип бинарное отношение. Примером может служить отношение «равно», потому что если а = б верно тогда б = а тоже верно. Формально бинарное отношение р через набор Икс симметрично, если:

{ displaystyle forall a, b in X (aRb Leftrightarrow bRa).}

Если р^Т представляет разговаривать из р, тогда р симметричен тогда и только тогда, когда р = р^Т.

Симметрия вместе с рефлексивность и транзитивность, являются тремя определяющими свойствами отношение эквивалентности.

Примеры

По математике

"равно" (равенство ) (тогда как "меньше" не является симметричным)
"является сопоставимый к ", для элементов частично заказанный набор
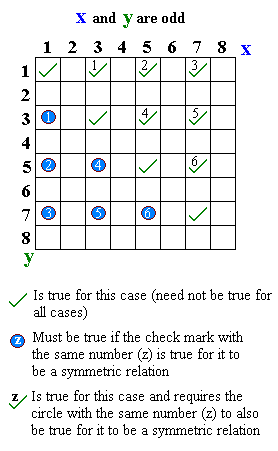
"... и ... нечетные":

Вне математики

«женат на» (в большинстве правовых систем)
"является полностью биологическим братом"
"это омофон из"
"сотрудник"
"товарищ по команде"

Связь с асимметричными и антисимметричными отношениями

По определению непустое отношение не может быть одновременно симметричным и одновременно симметричным. асимметричный (где если а относится к б, тогда б не может быть связано с а (точно так же)). Однако отношение не может быть ни симметричным, ни асимметричным, как в случае «меньше или равно» и «охотится»).

Симметричный и антисимметричный (где единственный способ а может быть связано с б и б иметь отношение а если а = б) фактически независимы друг от друга, как показывают эти примеры.

Математические примеры
	Симметричный	Не симметричный
Антисимметричный	равенство	"меньше или равно"
Не антисимметричный	соответствие в модульная арифметика	"делится на" по набору целых чисел

Нематематические примеры
	Симметричный	Не симметричный
Антисимметричный	"такой же человек, как и женат"	"является множественным числом"
Не антисимметричный	"является полным биологическим братом"	"охотится"

Характеристики

Симметричный и переходное отношение всегда квазирефлексивный.

Симметричный, транзитивный и рефлексивное отношение называется отношение эквивалентности.

Один из способов концептуализировать симметричное отношение в теории графов состоит в том, что симметричное отношение - это ребро, причем две вершины ребра являются двумя объектами, связанными таким образом. Таким образом, симметричные отношения и неориентированные графы являются комбинаторно эквивалентными объектами.