Решетка (заказ) - Lattice (order)
Эта статья включает в себя список общих Рекомендации, но он остается в основном непроверенным, потому что ему не хватает соответствующих встроенные цитаты. (Май 2009 г.) (Узнайте, как и когда удалить этот шаблон сообщения) |
| Бинарные отношения | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| А "✓"означает, что свойство столбца требуется в определении строки. Например, определение отношения эквивалентности требует, чтобы оно было симметричным. Все определения молчаливо требуют транзитивность и рефлексивность. |
| Алгебраические структуры |
|---|
А решетка абстрактная структура, изучаемая в математический субдисциплины теория порядка и абстрактная алгебра. Он состоит из частично заказанный набор в котором каждые два элемента имеют уникальный супремум (также называется наименьшей верхней границей или присоединиться ) и уникальный инфимум (также называется точной нижней границей или встреча ). Пример дается натуральные числа, частично заказано делимость, для которого единственным супремумом является наименьший общий множитель а единственная точная нижняя грань - это наибольший общий делитель.
Решетки также можно охарактеризовать как алгебраические структуры удовлетворение определенных аксиоматический идентичности. Поскольку эти два определения эквивалентны, теория решеток опирается на оба теория порядка и универсальная алгебра. Полурешетки включают решетки, которые, в свою очередь, включают Heyting и Булевы алгебры. Все эти «решетчатые» структуры допускают теоретико-порядковый а также алгебраические описания.
Решетки как частично упорядоченные множества
Если (L, ≤) это частично заказанный набор (посет), и S ⊆ L - произвольное подмножество, то элемент ты ∈ L считается верхняя граница из S если s ≤ ты для каждого s ∈ S. У набора может быть много верхних границ или вообще не быть. Верхняя граница ты из S как говорят, его наименьшая верхняя граница, или же присоединиться, или же супремум, если ты ≤ Икс для каждой верхней границы Икс из S. У набора не обязательно должна быть наименьшая верхняя граница, но не может быть более одной. Вдвойне, л ∈ L считается нижняя граница из S если л ≤ s для каждого s ∈ S. Нижняя граница л из S как говорят, его наибольшая нижняя граница, или же встреча, или же инфимум, если Икс ≤ л для каждой нижней границы Икс из S. Набор может иметь много нижних границ или не иметь вовсе, но может иметь не более одной наибольшей нижней границы.
Частично заказанный набор (L, ≤) называется стыковочная полурешетка если каждое двухэлементное подмножество {а, б} ⊆ L имеет соединение (т.е. наименьшую верхнюю границу) и называется встречная полурешетка если каждое двухэлементное подмножество имеет пересечение (то есть точную нижнюю границу), обозначенную а ∨ б и а ∧ б соответственно. (L, ≤) называется решетка если это и стыковочная, и встречная полурешетка. Это определение делает ∨ и ∧ бинарные операции. Обе операции монотонны относительно заданного порядка: а1 ≤ а2 и б1 ≤ б2 подразумевает, что а1 ∨ б1 ≤ а2 ∨ б2 и а1 ∧ б1 ≤ а2 ∧ б2.
Далее следует индукция аргумент, что каждое непустое конечное подмножество решетки имеет точную верхнюю границу и точную нижнюю границу. При дополнительных предположениях возможны дальнейшие выводы; видеть Полнота (теория порядка) для более подробного обсуждения этой темы. В этой статье также обсуждается, как можно перефразировать приведенное выше определение с точки зрения существования подходящих Связи Галуа между связанными частично упорядоченными множествами - подход, представляющий особый интерес для теоретико-категорийный приближения к решеткам, а для формальный анализ концепции.
А ограниченная решетка решетка, которая дополнительно имеет величайший элемент (также называемый максимум, или же верх элемент, и обозначается 1 или ) и наименее элемент (также называемый минимум, или же дно, обозначаемый 0 или ), которые удовлетворяют
- 0 ≤ Икс ≤ 1 для каждого Икс в L.
Каждую решетку можно вложить в ограниченную решетку, добавив искусственный наибольший и наименьший элемент, и каждая непустая конечная решетка ограничена, взяв соединение (соответственно, пересечение) всех элементов, обозначенное (соответственно ) где .
Частично упорядоченное множество является ограниченной решеткой тогда и только тогда, когда каждый конечный набор элементов (включая пустой набор) имеет соединение и пересечение. Для каждого элемента Икс посета это тривиально верно (это пустая правда ) который и, и, следовательно, каждый элемент poset является одновременно верхней и нижней границей пустого множества. Это означает, что объединение пустого множества является наименьшим элементом , а встреча пустого множества - наибольший элемент . Это согласуется с ассоциативностью и коммутативностью встречи и соединения: объединение объединения конечных множеств равно объединению объединений множеств, и, вдвойне, соединение объединения конечных множеств равно объединению объединений конечных множеств. пересечения множеств, т. е. для конечных подмножеств А и B посета L,
и
держать. Принимая B быть пустым множеством,
и
что согласуется с тем, что .
Элемент решетки у говорят крышка другой элемент Икс, если у > Икс, но не существует z такой, что у > z > Икс.Здесь, у > Икс означает Икс ≤ у и Икс ≠ у.
Решетка (L, ≤) называется оцененныйиногда в рейтинге (но см. Ранговый посет для альтернативного значения), если он может быть оснащен функция ранга р из L до ℕ, иногда до ℤ, совместимого с порядком (так р(Икс) < р(у) всякий раз, когда Икс < у) такой, что всякий раз, когда у крышки Икс, тогда р(у) = р(Икс) + 1. Значение ранговой функции для элемента решетки называется ее классифицировать.
Учитывая подмножество решетки, ЧАС ⊆ L, встретиться и присоединиться к частичные функции - они не определены, если их значение не входит в подмножество ЧАС. Полученная структура на ЧАС называется частичная решетка. В дополнение к этому внешнему определению как подмножество некоторой другой алгебраической структуры (решетки), частичная решетка также может быть внутренне определена как набор с двумя частичными бинарными операциями, удовлетворяющими определенным аксиомам.[1]
Решетки как алгебраические структуры
Общая решетка
An алгебраическая структура , состоящий из набора и два бинарных, коммутативных и ассоциативных операции , и , на это решетка если для всех элементов верны следующие аксиоматические тождества иногда называют законы поглощения.
Следующие два тождества также обычно рассматриваются как аксиомы, даже если они следуют из двух законов поглощения, взятых вместе.[примечание 1]. Они называются идемпотентные законы.
Эти аксиомы утверждают, что обе и находятся полурешетки. Законы поглощения, единственные вышеупомянутые аксиомы, в которых встречаются и встречаются, и соединяются, отличают решетку от произвольной пары полурешеточных структур и гарантируют, что две полурешетки взаимодействуют соответствующим образом. В частности, каждая полурешетка является двойной другого.
Ограниченная решетка
А ограниченная решетка является алгебраической структурой вида такой, что решетка, (дно решетки) - это элемент идентичности для операции соединения , и (вершина решетки) является единичным элементом для операции встречи .
Видеть полурешетка для получения дополнительной информации.
Связь с другими алгебраическими структурами
Решетки имеют некоторые связи с семейством групповые алгебраические структуры. Поскольку meet и join и коммутируют, и ассоциируют, решетку можно рассматривать как состоящую из двух коммутативных полугруппы с тем же доменом. Для ограниченной решетки эти полугруппы фактически коммутативны. моноиды. В закон поглощения - единственное определяющее тождество, присущее теории решеток.
По коммутативности, ассоциативности и идемпотентности можно думать о соединении и встрече как об операциях над непустыми конечными множествами, а не над парами элементов. В ограниченной решетке соединение и пересечение пустого множества также могут быть определены (как и , соответственно). Это делает ограниченные решетки несколько более естественными, чем решетки общего вида, и многие авторы требуют, чтобы все решетки были ограниченными.
Алгебраическая интерпретация решеток играет существенную роль в универсальная алгебра.
Связь между двумя определениями
Теоретико-порядковая решетка порождает две бинарные операции ∨ и. Поскольку коммутативные, ассоциативные законы и законы поглощения могут быть легко проверены для этих операций, они делают (L, ∨, ∧) в решетку в алгебраическом смысле.
Обратное также верно. Для алгебраически определенной решетки (L, ∨, ∧), можно определить частичный порядок ≤ на L установив
- а ≤ б если а = а ∧ б, или же
- а ≤ б если б = а ∨ б,
для всех элементов а и б из L. Законы поглощения гарантируют, что оба определения эквивалентны:
а = а ∧ б подразумевает б = б ∨ (б ∧ а) = (а ∧ б) ∨ б = а ∨ б
и вдвойне в другом направлении.
Теперь можно проверить, что отношение ≤, введенное таким образом, определяет частичный порядок, в котором двоичные встречи и соединения задаются посредством исходных операций ∨ и ∧.
Поскольку два определения решетки эквивалентны, можно свободно использовать аспекты любого определения любым способом, который соответствует поставленной цели.
Примеры

Рис. 1: Подмножества {x, y, z}, под установить включение. Название «решетка» подсказано формой Диаграмма Хассе изображая это.

Рис. 2: Решетка целых делителей 60 в порядке "разделяет".

Рис. 3: Решетка из перегородки из {1, 2, 3, 4}, заказан "уточняет".

Рис. 4: Решетка натуральных чисел, упорядоченная по ≤.

Рис. 5: Решетка из неотрицательных целочисленных пар, упорядоченная покомпонентно.
- Для любого набора А, совокупность всех подмножеств А (называется набор мощности из А) можно заказать через включение подмножества получить решетку, ограниченную А сам и пустой набор. Набор пересечение и союз интерпретировать meet и join соответственно (см. рис. 1).
- Для любого набора А, совокупность всех конечных подмножеств А, упорядоченная по включению, также является решеткой и будет ограниченной тогда и только тогда, когда А конечно.
- Для любого набора А, собрание всех перегородки из А, заказан уточнение, является решеткой (см. рис. 3).
- В положительные целые числа в их обычном порядке образуют решетку при операциях «min» и «max». 1 - нижний; верха нет (см. рис. 4).
- В Декартов квадрат натуральных чисел, упорядоченных так, чтобы (а, б) ≤ (c, d) если а ≤ c и б ≤ d. Пара (0, 0) это нижний элемент; верха нет (см. рис. 5).
- Натуральные числа также образуют решетку при операциях взятия наибольший общий делитель и наименьший общий множитель, с участием делимость как отношение порядка: а ≤ б если а разделяет б. 1 - нижний; 0 - верх. Рис. 2 показана конечная подрешетка.
- Каждые полная решетка (также см ниже ) является (довольно специфической) ограниченной решеткой. Этот класс дает начало широкому спектру практических Примеры.
- Набор компактные элементы из арифметика Полная решетка - это решетка с наименьшим элементом, в которой операции решетки задаются ограничением соответствующих операций арифметической решетки. Это особое свойство, которое отличает арифметические решетки от алгебраические решетки, для которых компакты только образуют стыковочная полурешетка. Оба эти класса полных решеток изучаются в теория предметной области.
Дополнительные примеры решеток приведены для каждого из дополнительных свойств, обсуждаемых ниже.
Примеры нерешеток
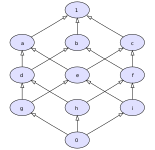 Рис. 8: Безрешеточный посет: а и б имеют общие нижние границы 0, d, грамм, час, и я, но ни один из них не наибольшая нижняя граница. |
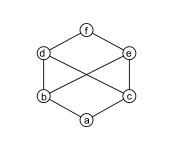 Рис. 7: Безрешеточный посет: б и c имеют общие верхние границы d, е, и ж, но ни один из них не наименьшая верхняя граница. |
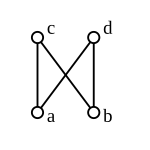 Рис. 6: Безрешеточный посет: c и d не имеют общей верхней границы. |
Большинство частично упорядоченных множеств не являются решетками, в том числе следующие.
- Дискретный позет, означающий такой позет, что Икс ≤ у подразумевает Икс = у, является решеткой тогда и только тогда, когда она имеет не более одного элемента. В частности, двухэлементное дискретное множество не является решеткой.
- Хотя набор {1, 2, 3, 6} частично упорядоченная по делимости решетка, множество {1, 2, 3} так упорядоченный не является решеткой, потому что пара 2, 3 не имеет соединения; аналогично, 2, 3 не хватает встречи в {2, 3, 6}.
- Набор {1, 2, 3, 12, 18, 36} частично упорядоченный по делимости не является решеткой. Каждая пара элементов имеет верхнюю границу и нижнюю границу, но пара 2, 3 имеет три верхние границы, а именно 12, 18 и 36, ни одна из которых не является наименьшей из этих трех при делимости (12 и 18 не делятся друг друга). Точно так же пара 12, 18 имеет три нижние границы, а именно 1, 2 и 3, ни одна из которых не является наибольшей из этих трех при делимости (2 и 3 не делят друг друга).
Морфизмы решеток

Соответствующее понятие морфизм между двумя решетками легко течет из над алгебраическое определение. Даны две решетки (L, ∨L, ∧L) и (M, ∨M, ∧M), а решеточный гомоморфизм из L к M это функция ж : L → M такое, что для всех а, б ∈ L:
- ж(а ∨L б) = ж(а) ∨M ж(б), и
- ж(а ∧L б) = ж(а) ∧M ж(б).
Таким образом ж это гомоморфизм из двух основных полурешетки. Когда рассматриваются решетки с большей структурой, морфизмы также должны «уважать» дополнительную структуру. В частности, гомоморфизм ограниченной решетки (обычно называется просто «решеточный гомоморфизм») ж между двумя ограниченными решетками L и M также должен обладать следующим свойством:
- ж(0L) = 0M , и
- ж(1L) = 1M .
В теоретико-порядковой формулировке эти условия просто утверждают, что гомоморфизм решеток является функцией сохранение двоичный встречается и присоединяется. Для ограниченных решеток сохранение наименьшего и наибольшего элементов - это просто сохранение соединения и встречи пустого множества.
Любой гомоморфизм решеток обязательно монотонный относительно связанного отношения порядка; видеть Функция сохранения предела. Обратное неверно: монотонность отнюдь не означает требуемого сохранения встреч и стыков (см. Рис.9), хотя сохраняющий порядок биекция является гомоморфизмом, если его обратный также сохраняет порядок.
Учитывая стандартное определение изоморфизмы как обратимые морфизмы, a решеточный изоморфизм это просто биективный решеточный гомоморфизм. Аналогично решеточный эндоморфизм является решеточным гомоморфизмом решетки в себя, а решеточный автоморфизм является биективным решеточным эндоморфизмом. Решетки и их гомоморфизмы образуют категория.
Подрешетки
А подрешетка решетки L это подмножество L это решетка с теми же операциями пересечения и соединения, что и L. То есть, если L решетка и M это подмножество L такое, что для каждой пары элементов а, б в M обе а ∧ б и а ∨ б находятся в M, тогда M является подрешеткой L.[2]
Подрешетка M решетки L это выпуклая подрешетка из L, если Икс ≤ z ≤ у и Икс, у в M подразумевает, что z принадлежит M, для всех элементов Икс, у, z в L.
Свойства решеток
Теперь мы введем ряд важных свойств, которые приводят к интересным специальным классам решеток. Один из них - ограниченность - уже обсуждался.
Полнота
Посет называется полная решетка если все его подмножества имеют как соединение, так и встречу. В частности, всякая полная решетка является ограниченной решеткой. В то время как ограниченные решеточные гомоморфизмы в общем случае сохраняют только конечные соединения и пересечения, полные решеточные гомоморфизмы требуются для сохранения произвольных соединений и пересечений.
Каждый ч.у., являющийся полной полурешеткой, также является полной решеткой. С этим результатом связано интересное явление, заключающееся в том, что существуют различные конкурирующие понятия гомоморфизма для этого класса множеств, в зависимости от того, рассматриваются ли они как полные решетки, полные соединения-полурешетки, полные пересекающиеся полурешетки, либо как полные соединения, либо как пересекающиеся полные решетки.
Обратите внимание, что «частичная решетка» не является противоположностью «полной решетки» - скорее, «частичная решетка», «решетка» и «полная решетка» становятся все более ограничительными определениями.
Условная полнота
А условно полная решетка является решеткой, в которой каждый непустой подмножество который имеет верхнюю границу имеет соединение (т. е. точную верхнюю границу). Такие решетки дают наиболее прямое обобщение аксиома полноты из действительные числа. Условно полная решетка - это либо полная решетка, либо полная решетка без максимального элемента 1, минимального элемента 0 или обоих.
Распределительность
 Рис. 11: Наименьшая немодулярная (и, следовательно, недистрибутивная) решетка N5. Обозначенные элементы нарушают уравнение дистрибутивности c ∧ (а ∨ б) = (c ∧ а) ∨ (c ∧ б), но удовлетворить его двойную c ∨ (а ∧ б) = (c ∨ а) ∧ (c ∨ б). |
 Рис. 10: Наименьшая недистрибутивная (но модульная) решетка M3. |
Поскольку решетки имеют две бинарные операции, естественно спросить, не является ли одна из них распределяет над другим, то есть одно или другое из следующих двойной законы справедливы для каждых трех элементов а, б, c из L:
- Распределимость ∨ над ∨
- а ∨ (б ∧ c) = (а ∨ б) ∧ (а ∨ c).
- Распределимость ∧ над ∧
- а ∧ (б ∨ c) = (а ∧ б) ∨ (а ∧ c).
Решетка, удовлетворяющая первой или, что эквивалентно (как выясняется), второй аксиоме, называется распределительная решеткаЕдинственные недистрибутивные решетки, содержащие менее 6 элементов, называются M3 и н5;[3] они показаны на Рисунках 10 и 11 соответственно. Решетка дистрибутивна тогда и только тогда, когда она не имеет подрешетка изоморфна M3 или N5.[4] Каждая дистрибутивная решетка изоморфна решетке множеств (с объединением и пересечением как соединением и соединением соответственно).[5]
Для обзора более сильных понятий дистрибутивности, которые подходят для полных решеток и которые используются для определения более специальных классов решеток, таких как кадры и полностью распределительные решетки, видеть распределительность в теории порядка.
Модульность
Для некоторых приложений условие дистрибутивности слишком сильное, и часто бывает полезно следующее более слабое свойство. Решетка (L, ∨, ∧) является модульный если для всех элементов а, б, c из L, выполняется следующее тождество.
- Модульная идентичность
- (а ∧ c) ∨ (б ∧ c) = ((а ∧ c) ∨ б) ∧ c.
Это условие эквивалентно следующей аксиоме.
- Модульное право
- а ≤ c подразумевает а ∨ (б ∧ c) = (а ∨ б) ∧ c.
Решетка является модульной тогда и только тогда, когда она не имеет подрешетка изоморфен N5 (показано на рис. 11).[4] Помимо дистрибутивных решеток, примерами модульных решеток являются решетки двусторонние идеалы из звенеть, решетка подмодулей модуль, а решетка нормальные подгруппы из группа. В набор условий первого порядка с заказом "более конкретен, чем"- немодульная решетка, используемая в автоматическое рассуждение.
Полумодулярность
Конечная решетка является модульной тогда и только тогда, когда она одновременно верхняя и нижняя. полумодульный. Для градуированной решетки (верхняя) полумодулярность эквивалентна следующему условию на ранговую функцию р:
- р(Икс) + р(у) ≥ р(Икс ∧ у) + р(Икс ∨ у).
Еще одно эквивалентное (для градуированных решеток) условие: Биркофф состояние:
- для каждого Икс и у в L, если Икс и у оба покрывают Икс ∧ у, тогда Икс ∨ у охватывает оба Икс и у.
Решетка называется полумодулярной снизу, если двойственная к ней полумодулярна. Для конечных решеток это означает, что предыдущие условия выполняются с заменой ∨ и, заменой «покрытий» на «покрывается посредством» и обращением неравенств.[6]
Непрерывность и алгебраичность
В теория предметной области, естественно стремиться аппроксимировать элементы в частичном порядке «гораздо более простыми» элементами. Это приводит к классу непрерывные позы, состоящий из множеств, где каждый элемент может быть получен как супремум направленный набор элементов, которые путь ниже элемент. Если можно дополнительно ограничить их компактные элементы чугуна для получения этих направленных множеств, то чётное множество алгебраический. Обе концепции могут быть применены к решеткам следующим образом:
- А непрерывная решетка является полной решеткой, непрерывной как ч.у.
- An алгебраическая решетка является полной решеткой, алгебраической как ЧУМ.
Оба эти класса обладают интересными свойствами. Например, непрерывные решетки можно охарактеризовать как алгебраические структуры (с бесконечными операциями), удовлетворяющие определенным тождествам. Хотя такая характеристика не известна для алгебраических решеток, их можно описать «синтаксически» с помощью Информационные системы Скотта.
Дополнения и псевдодополнения
Позволять L - ограниченная решетка с наибольшим элементом 1 и наименьшим элементом 0. Два элемента Икс и у из L находятся дополняет друг друга тогда и только тогда, когда:
- Икс ∨ у = 1 и Икс ∧ у = 0.
В общем, некоторые элементы ограниченной решетки могут не иметь дополнения, а другие могут иметь более одного дополнения. Например, множество {0, ½, 1} с его обычным порядком является ограниченной решеткой, а ½ не имеет дополнения. В ограниченной решетке N5, элемент а имеет два дополнения, а именно. б и c (см. рис. 11). Ограниченная решетка, каждый элемент которой имеет дополнение, называется дополненная решетка.
Дополняемая решетка, которая также является дистрибутивной, называется Булева алгебра. Для распределительной решетки дополнение к Икс, когда он существует, уникален.
В случае уникальности дополнения пишем ¬Икс = у и эквивалентно ¬у = Икс. Соответствующий унарный операция над L, называемое дополнением, вводит аналог логического отрицание в теорию решетки.
Гейтинговые алгебры являются примером распределительных решеток, в которых некоторые элементы могут не иметь дополнений. Каждый элемент Икс алгебры Гейтинга, с другой стороны, псевдодополнение, также обозначается ¬Икс. Псевдодополнение - величайший элемент у такой, что Икс ∧ у = 0. Если псевдодополнение каждого элемента алгебры Гейтинга на самом деле является дополнением, то алгебра Гейтинга на самом деле является булевой алгеброй.
Условие цепи Джордана – Дедекинда
А цепь из Икс0 к Иксп это набор , где . длина этой цепочки п, или на единицу меньше, чем его количество элементов. Цепь максимальный если Икся крышки Икся−1 для всех 1 ≤ я ≤ п.
Если для любой пары, Икс и у, где Икс < у, все максимальные цепи из Икс к у одинаковой длины, то говорят, что решетка удовлетворяет условию Условие цепи Джордана – Дедекинда.
Бесплатные решетки
Любой набор Икс может использоваться для создания свободная полурешетка FX. Свободная полурешетка определяется как состоящая из всех конечных подмножеств Икс, с полурешеточной операцией, задаваемой обычными установить союз. Свободная полурешетка имеет универсальная собственность. Для свободная решетка над набором Икс, Whitman дал конструкцию, основанную на многочленах над Икс'члены s.[7][8]
Важные теоретико-решеточные понятия
Теперь мы определим некоторые теоретико-порядковые понятия, важные для теории решеток. Далее пусть Икс быть элементом некоторой решетки L. Если L имеет нижний элемент 0, Икс ≠ 0 иногда требуется. Икс называется:
- Присоединяйтесь к несократимому если Икс = а ∨ б подразумевает Икс = а или Икс = б для всех а, б в L. Когда первое условие обобщается на произвольные соединения , Икс называется полностью присоединиться к неприводимому (или ∨-неприводимый). Двойственное понятие встретить несводимость (∧-неприводимый). Например, на рис. 2, элементы 2, 3, 4 и 5 являются неприводимыми к соединению, а элементы 12, 15, 20 и 30 - неприводимыми. В решетке действительные числа при обычном порядке каждый элемент является неприводимым к соединению, но ни один элемент не является полностью неприводимым к соединению.
- Присоединяйтесь к прайму если Икс ≤ а ∨ б подразумевает Икс ≤ а или Икс ≤ б. Это тоже можно обобщить, чтобы получить понятие полностью присоединиться к прайму. Двойственное понятие встретить премьер. Каждый элемент с простым соединением также является неприводимым по соединению, и каждый элемент с простым соединением также является неприводимым. Обратное верно, если L является распределительным.
Позволять L имеют нижний элемент 0. Элемент Икс из L является атом если 0 < Икс и не существует элемента у из L такой, что 0 < у < Икс. потом L называется:
- Атомный если для каждого ненулевого элемента Икс из L, существует атом а из L такой, что а ≤ Икс;
- Атомистический если каждый элемент L это супремум атомов.
Представления о идеалы и двойственное понятие фильтры относятся к конкретным видам подмножества частично упорядоченного множества и поэтому важны для теории решеток. Подробности можно найти в соответствующих записях.
Смотрите также
- Присоединяйтесь и знакомьтесь
- Карта решеток
- Ортодополненная решетка
- Общий заказ
- Идеально и фильтр (двойственные понятия)
- Косая решетка (обобщение до некоммутативного соединения и встречи)
- Решетка Эйлера
- Решетка столба
- Решетка Тамари
- Решетка Юнга – Фибоначчи
- 0,1-простая решетка
Приложения, использующие теорию решеток
Обратите внимание, что во многих приложениях наборы представляют собой только частичные решетки: не каждая пара элементов имеет пересечение или соединение.
- Бессмысленная топология
- Решетка подгрупп
- Спектральное пространство
- Инвариантное подпространство
- Оператор закрытия
- Абстрактная интерпретация
- Решетка поглощения
- Нечеткое множество теория
- Алгебраизации логики первого порядка
- Семантика языков программирования
- Теория предметной области
- Онтология (информатика)
- Множественное наследование
- Формальный анализ концепции и решетчатый майнер (теория и инструмент)
- Фильтр Блума
- Поток информации
- Порядковая оптимизация
- Квантовая логика
- Медианный график
- Пространство знаний
- Регулярное изучение языка
- Аналогичное моделирование
Примечания
- ^ а ∨ а = а ∨ (а ∧ (а ∨ а)) = а, и вдвойне для другого идемпотентного закона. Дедекинд, Ричард (1897 г.), "Uber Zerlegungen von Zahlen durch ihre grössten gemeinsamen Teiler", Braunschweiger Festschrift: 1–40.
Рекомендации
- ^ Grätzer 1996, п.52.
- ^ Беррис, Стэнли Н. и Санкаппанавар, Х. П., 1981. Курс универсальной алгебры. Springer-Verlag. ISBN 3-540-90578-2.
- ^ Дэйви и Пристли (2002), Упражнение 4.1, п. 104.
- ^ а б Дэйви и Пристли (2002), Теорема 4.10, п. 89.
- ^ Дэйви и Пристли (2002), Теорема 10.21, стр. 238–239.
- ^ Стэнли, Ричард П., Перечислительная комбинаторика (том 1), Cambridge University Press, стр. 103–104, ISBN 0-521-66351-2
- ^ Филип Уитмен (1941). «Свободные решетки I». Анналы математики. 42: 325–329. Дои:10.2307/1969001.
- ^ Филип Уитмен (1942). «Свободные решетки II». Анналы математики. 43: 104–115. Дои:10.2307/1968883.
Монографии доступны бесплатно онлайн:
- Беррис, Стэнли Н. и Санкаппанавар, Х. П., 1981. Курс универсальной алгебры. Springer-Verlag. ISBN 3-540-90578-2.
- Джипсен, Питер и Генри Роуз, Разновидности решеток, Конспект лекций по математике 1533, Springer Verlag, 1992. ISBN 0-387-56314-8.
- Нация, Дж. Б., Заметки по теории решеток. Главы 1-6. Главы 7–12; Приложения 1–3.
Элементарные тексты рекомендуются тем, у кого ограниченное математическая зрелость:
- Доннеллан, Томас, 1968 год. Теория решеток. Пергамон.
- Гретцер, Джордж, 1971. Теория решеток: первые концепции и распределительные решетки. В. Х. Фриман.
Стандартный современный вводный текст, несколько сложнее, чем приведенный выше:
- Davey, B.A .; Пристли, Х.А. (2002), Введение в решетки и порядок, Издательство Кембриджского университета, ISBN 978-0-521-78451-1
Продвинутые монографии:
- Гаррет Биркофф, 1967. Теория решеток, 3-е изд. Vol. 25 публикаций коллоквиума AMS. Американское математическое общество.
- Роберт П. Дилворт и Кроули, Питер, 1973. Алгебраическая теория решеток. Прентис-Холл. ISBN 978-0-13-022269-5.
- Гретцер, Джордж (1996) [1978]. Общая теория решеток (Второе изд.). Базель: Биркхойзер. ISBN 978-3-7643-6996-5.
На свободных решетках:
- Р. Фриз, Дж. Джезек и Дж. Б. Нэйшн, 1985. "Свободные решетки". Математические обзоры и монографии Vol. 42. Математическая ассоциация Америки.
- Джонстон, П. Т., 1982. Каменные пространства. Кембриджские исследования в области высшей математики 3. Издательство Кембриджского университета.
К истории теории решеток:
- Štĕpánka Bilová (2001). Эдуард Фукс (ред.). Теория решеток - ее рождение и жизнь (PDF). Прометей. С. 250–257.
О приложениях теории решетки:
- Гаррет Биркгоф (1967). Джеймс С. Эббот (ред.). Что решетки могут для вас сделать?. Ван Ностранд. Оглавление
внешняя ссылка
- «Решеточно-упорядоченная группа», Энциклопедия математики, EMS Press, 2001 [1994]
- Вайсштейн, Эрик В. "Решетка". MathWorld.
- J.B. Nation, Заметки по теории решеток, неопубликованные примечания к курсу доступны в виде двух файлов PDF.
- Ральф Фриз, "Домашняя страница теории решеток".
- OEIS последовательность A006966 (Количество немеченых решеток с п элементы)






































