Решетка подгрупп - Википедия - Lattice of subgroups
В математика, то решетка подгрупп из группа это решетка чьими элементами являются подгруппы из , с частичный заказ связь существование установить включение В этой решетке объединением двух подгрупп является подгруппа генерируется по их союз, а встреча двух подгрупп - это их пересечение.
Пример
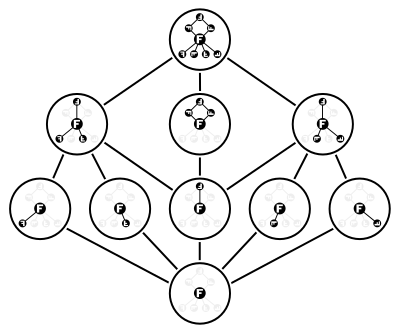
В группа диэдра Dih4 имеет десять подгрупп, считая себя и тривиальная подгруппа. Пять из восьми элементов группы порождают подгруппы второго порядка, а два других неидентичных элемента генерируют одинаковые циклический подгруппа четвертого порядка. Кроме того, есть две подгруппы вида Z2 × Z2, порожденный парами элементов второго порядка. Решетка, образованная этими десятью подгруппами, показана на рисунке.
Этот пример также показывает, что решетка всех подгрупп группы не является модульная решетка в целом. Действительно, эта конкретная решетка содержит запрещенный «пятиугольник» N5 как подрешетка.
Характеристики
Для любого А, B, и C подгруппы группы с А ≤ C (А подгруппа C) тогда AB ∩ C = А (В ∩ С); умножение здесь произведение подгрупп. Это свойство было названо модульное свойство групп (Ашбахер 2000 ) или же (Дедекинд s) модульный закон (Робинсон 1996, Кон 2000 ). Поскольку для двух нормальных подгрупп продукт на самом деле является наименьшей подгруппой, содержащей эти две, нормальные подгруппы образуют модульная решетка.
В Теорема о решетке устанавливает Связь Галуа между решеткой подгрупп группы и решеткой ее частных.
В Лемма Цассенхауза дает изоморфизм между некоторыми комбинациями частных и произведений в решетке подгрупп.
Вообще говоря, на форму решетки подгрупп нет ограничений в том смысле, что каждая решетка изоморфна подрешетке решетки подгрупп некоторой группы. Кроме того, каждый конечный решетка изоморфна подрешетке решетки подгрупп некоторого конечная группа (Шмидт 1994, п. 9).
Характеристические решетки
Подгруппы с определенными свойствами образуют решетки, а другие - нет.
- Нормальные подгруппы всегда образуют модульную решетку. Фактически, существенное свойство, которое гарантирует, что решетка является модульной, состоит в том, что подгруппы коммутируют друг с другом, т.е. квазинормальные подгруппы.
- Нильпотентный нормальные подгруппы образуют решетку, которая является (частью) содержанием Теорема Фиттинга.
- В общем, для любого класса Фиттинга F, как субнормальный F-подгруппы и нормальные F-подгруппы образуют решетки. Это включает в себя вышеуказанное с F класс нильпотентных групп, а также другие примеры, такие как F класс разрешимые группы. Класс групп называется классом Фиттинга, если он замкнут относительно изоморфизма, субнормальных подгрупп и произведений субнормальных подгрупп.
- Центральная подгруппы образуют решетку.
Однако ни конечные подгруппы, ни подгруппы кручения не образуют решетку: например, бесплатный продукт порождается двумя элементами кручения, но бесконечен и содержит элементы бесконечного порядка.
Тот факт, что нормальные подгруппы образуют модулярную решетку, является частным случаем более общего результата, а именно того, что в любом Сорт Мальцева (из которых группы являются примером), решетка конгруэнций модульный (Кернс и поцелуй 2013 ).
Характеризация групп решетками их подгрупп
Теоретическая информация о решетке подгрупп иногда может использоваться для вывода информации об исходной группе, идея, которая восходит к работе Øystein Ore (1937, 1938 ). Например, как доказал Оре, группа локально циклический тогда и только тогда, когда его решетка подгрупп распределительный. Если дополнительно решетка удовлетворяет условие возрастающей цепи, то группа циклическая.
Группы, решетка подгрупп которых является дополненная решетка называются дополненные группы (Захер 1953 ), а группы, решетка подгрупп которых модульные решетки называются Группы Ивасавы или модульные группы (Ивасава 1941 ). Теоретико-решеточные характеристики этого типа существуют также для разрешимые группы и идеальные группы (Suzuki 1951 года ).
Рекомендации
- Ашбахер, М. (2000). Теория конечных групп. Издательство Кембриджского университета. п. 6. ISBN 978-0-521-78675-1.CS1 maint: ref = harv (связь)
- Баер, Рейнхольд (1939). «Значение системы подгрупп для структуры группы». Американский журнал математики. Издательство Университета Джона Хопкинса. 61 (1): 1–44. Дои:10.2307/2371383. JSTOR 2371383.CS1 maint: ref = harv (связь)
- Кон, Пол Мориц (2000). Классическая алгебра. Вайли. п. 248. ISBN 978-0-471-87731-8.CS1 maint: ref = harv (связь)
- Ивасава, Кенкити (1941), "Über die endlichen Gruppen und die Verbände ihrer Untergruppen", J. Fac. Sci. Imp. Univ. Токио. Разд. Я., 4: 171–199, МИСТЕР 0005721CS1 maint: ref = harv (связь)
- Кирнес, Кейт; Поцелуй, Эмиль В. (2013). Форма решеток конгруэнтности. American Mathematical Soc. п. 3. ISBN 978-0-8218-8323-5.CS1 maint: ref = harv (связь)
- Руда, Эйстейн (1937). «Структуры и теория групп. I». Математический журнал герцога. 3 (2): 149–174. Дои:10.1215 / S0012-7094-37-00311-9. МИСТЕР 1545977.CS1 maint: ref = harv (связь)
- Руда, Эйстейн (1938). «Структуры и теория групп. II». Математический журнал герцога. 4 (2): 247–269. Дои:10.1215 / S0012-7094-38-00419-3. HDL:10338.dmlcz / 100155. МИСТЕР 1546048.CS1 maint: ref = harv (связь)
- Робинсон, Дерек (1996). Курс теории групп. Springer Science & Business Media. п. 15. ISBN 978-0-387-94461-6.CS1 maint: ref = harv (связь)
- Роттлендер, Ада (1928). "Nachweis der Existenz nicht-isomorpher Gruppen von gleicher Situation der Untergruppen". Mathematische Zeitschrift. 28 (1): 641–653. Дои:10.1007 / BF01181188.CS1 maint: ref = harv (связь)
- Шмидт, Роланд (1994). Подгрупповые решетки групп. Экспозиции по математике. 14. Вальтер де Грюйтер. ISBN 978-3-11-011213-9.CS1 maint: ref = harv (связь) Рассмотрение Ральфом Фризом в Быке. AMS 33 (4): 487–492.
- Сузуки, Мичио (1951). «О решетке подгрупп конечных групп». Труды Американского математического общества. Американское математическое общество. 70 (2): 345–371. Дои:10.2307/1990375. JSTOR 1990375.CS1 maint: ref = harv (связь)
- Сузуки, Мичио (1956). Структура группы и структура ее решетки подгрупп.. Берлин: Springer Verlag.
- Яковлев, Б. В. (1974). «Условия, при которых решетка изоморфна решетке подгрупп группы». Алгебра и логика. 13 (6): 400–412. Дои:10.1007 / BF01462952.CS1 maint: ref = harv (связь)
- Захер, Джованни (1953). "Caratterizzazione dei gruppi risolubili d'ordine finito complementati". Rendiconti del Seminario Matematico della Università di Padova. 22: 113–122. ISSN 0041-8994. МИСТЕР 0057878.CS1 maint: ref = harv (связь)


