Косая решетка - Skew lattice

В абстрактная алгебра, а косая решетка является алгебраическая структура это некоммутативный обобщение решетка. Хотя срок косая решетка может использоваться для обозначения любого некоммутативного обобщения решетки, с 1989 года он используется в основном следующим образом.

Определение

А косая решетка это набор S оснащен двумя ассоциативный, идемпотент бинарные операции ${ Displaystyle клин}$ и ${ displaystyle vee}$ , называется встретить и присоединиться, которые подтверждают следующую двойную пару законов поглощения

{ Displaystyle х клин (х ви у) = х = (у ви х) клин х}

,

{ Displaystyle х ви (х клин у) = х = (у клин х) ви х}

.

При условии ${ displaystyle vee}$ и ${ Displaystyle клин}$ ассоциативны и идемпотентны, эти тождества эквивалентны проверке следующей двойственной пары утверждений:

{ Displaystyle х ви у = х}

если

{ Displaystyle х клин у = у}

,

{ Displaystyle х клин у = х}

если

{ Displaystyle х ви у = у}

.^[1]

Историческое прошлое

На протяжении более 60 лет некоммутативные вариации решеток изучаются с разными мотивами. Для некоторых мотивацией был интерес к концептуальным границам теория решетки; для других это был поиск некоммутативных форм логика и Булева алгебра; а для других это было поведение идемпотенты в кольца. А некоммутативная решеткавообще говоря, это алгебра ${ Displaystyle (S; клин, vee)}$ куда ${ Displaystyle клин}$ и ${ displaystyle vee}$ находятся ассоциативный, идемпотент двоичный операции связаны личности поглощения гарантируя, что ${ Displaystyle клин}$ в некотором роде дуализирует ${ displaystyle vee}$ . Точные выбранные идентичности зависят от основной мотивации, при этом различные варианты выбора производят различные многообразия алгебр.

Паскуаль Джордан, мотивированные вопросами в квантовая логика, инициировал исследование некоммутативные решетки в своей статье 1949 г. Über Nichtkommutative Verbände,^[2] выбор тождеств поглощения

{ Displaystyle х клин (у ви х) = х = (х клин у) ви х.}

Он называл те алгебры, которые им удовлетворяют, как Schrägverbände. Изменяя или дополняя эти тождества, Джордан и другие получили ряд разновидностей некоммутативных решеток. Начиная с работы Джонатана Лича 1989 г., Перекос решеток в кольца,^[3] косые решетки, как определено выше, были основными объектами исследования. Этому способствовали предыдущие результаты о группы. Это особенно характерно для многих основных свойств.

Основные свойства

Естественный частичный порядок и естественный квазипорядок

В косой решетке ${ displaystyle S}$ , естественный частичный заказ определяется ${ displaystyle y leq x}$ если ${ Displaystyle х клин у = у = у клин х}$ , или дважды, ${ Displaystyle х vee y = x = y vee x}$ . Естественный Предварительный заказ на ${ displaystyle S}$ дан кем-то ${ Displaystyle у prevq х}$ если ${ Displaystyle у клин х клин у = у}$ или дважды ${ Displaystyle х ви у ви х = х}$ . Пока ${ displaystyle leq}$ и ${ displaystyle prevq}$ договориться о решетках, ${ displaystyle leq}$ правильно уточняет ${ displaystyle prevq}$ в некоммутативном случае. Индуцированная естественная эквивалентность ${ displaystyle D}$ определяется ${ displaystyle xDy}$ если ${ Displaystyle х предшествующий у предшествующий х}$ , то есть, ${ Displaystyle х клин у клин х = х}$ и ${ Displaystyle у клин х клин у = у}$ или дважды, ${ Displaystyle х ви у ви х = х}$ и ${ Displaystyle у ви х ви у = у}$ . Блоки перегородки ${ Displaystyle S / D}$ arelattice в порядке ${ displaystyle A> B}$ если ${ displaystyle a in A}$ и ${ displaystyle b in B}$ существуют такие, что ${ displaystyle a> b}$ . Это позволяет нам рисовать Диаграммы Хассе косых решеток, таких как следующая пара:

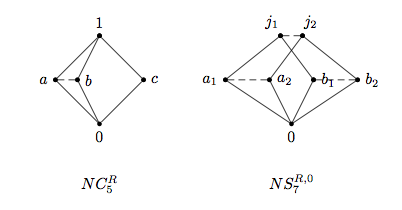
Например, на диаграмме слева вверху это ${ displaystyle a}$ и ${ displaystyle b}$ находятся ${ displaystyle D}$ Связанные обозначены пунктирным сегментом. Наклонные линии показывают естественный частичный порядок между элементами отдельных ${ displaystyle D}$ -классы. Элементы ${ displaystyle 1}$ , ${ displaystyle c}$ и ${ displaystyle 0}$ сформировать синглтон ${ displaystyle D}$ -классы.

Прямоугольные косые решетки

Косые решетки, состоящие из одного ${ displaystyle D}$ -класс называются прямоугольный. Для них характерны эквивалентные тождества: ${ Displaystyle х клин у клин х = х}$ , ${ Displaystyle у ви х ви у = у}$ и ${ Displaystyle х ви у = у клин х}$ . Прямоугольные косые решетки изоморфны косым решеткам, имеющим следующую конструкцию (и наоборот): заданные непустые множества ${ displaystyle L}$ и ${ displaystyle R}$ , на ${ displaystyle L times R}$ определять ${ Displaystyle (х, у) vee (г, ш) = (г, у)}$ и ${ Displaystyle (х, у) клин (г, ш) = (х, ш)}$ . В ${ displaystyle D}$ -классовое разбиение косой решетки ${ displaystyle S}$ , как показано на приведенных выше диаграммах, является единственным разбиением ${ displaystyle S}$ в свои максимальные прямоугольные подалгебры. Кроме того, ${ displaystyle D}$ является конгруэнцией с индуцированной фактор-алгеброй ${ Displaystyle S / D}$ максимальный решетчатый образ ${ displaystyle S}$ , таким образом делая каждую косую решетку ${ displaystyle S}$ решетка прямоугольных подалгебр. Это теорема Клиффорда – Маклина для косых решеток, впервые данная для полос отдельно Клиффорд и Маклин. Он также известен как Первая теорема разложения для косых решеток.

Правые (левые) косые решетки и факторизация Кимуры

Косая решетка является правой, если она удовлетворяет тождеству ${ Displaystyle х клин у клин х = у клин х}$ или дважды, ${ Displaystyle х ви у ви х = х ви у}$ Эти тождества по существу утверждают, что ${ Displaystyle х клин у = у}$ и ${ Displaystyle х ви у = х}$ в каждом ${ displaystyle D}$ -учебный класс. Каждая косая решетка ${ displaystyle S}$ имеет уникальное максимальное правостороннее изображение ${ Displaystyle S / L}$ где соответствие ${ displaystyle L}$ определяется ${ displaystyle xLy}$ если оба ${ Displaystyle х клин у = х}$ и ${ Displaystyle у клин х = у}$ (или дважды, ${ Displaystyle х ви у = у}$ и ${ Displaystyle у ви х = х}$ ). Точно так же косая решетка будет левой, если ${ Displaystyle х клин у = х}$ и ${ Displaystyle х ви у = у}$ в каждом ${ displaystyle D}$ -учебный класс. Снова максимальный левый образ косой решетки ${ displaystyle S}$ это изображение ${ Displaystyle S / R}$ где соответствие ${ displaystyle R}$ определяется двойным образом: ${ displaystyle L}$ . Многие примеры косых решеток могут быть правыми или левыми. В решетке конгруэнций ${ Displaystyle R vee L = D}$ и ${ Displaystyle R cap L}$ тождественное соответствие ${ displaystyle Delta}$ . Индуцированный эпиморфизм ${ Displaystyle S rightarrow S / D}$ факторов через оба индуцированных эпиморфизма ${ Displaystyle S rightarrow S / L}$ и ${ Displaystyle S rightarrow S / R}$ . Параметр ${ displaystyle T = S / D}$ , гомоморфизм ${ displaystyle k: S rightarrow S / L times S / R}$ определяется ${ Displaystyle к (х) = (L_ {x}, R_ {x})}$ , индуцирует изоморфизм ${ Displaystyle к *: S sim S / L times _ {T} S / R}$ . Это факторизация Кимуры ${ displaystyle S}$ в расслоенное произведение его максимальных правых и левых образов.

Подобно теореме Клиффорда – Маклина, факторизация Кимуры (или Вторая теорема о разложении косых решеток) был впервые дан для регулярных полос (удовлетворяющих среднему значению поглощения, ${ displaystyle xyxzx = xyzx}$ ). Действительно, оба ${ Displaystyle клин}$ и ${ displaystyle vee}$ являются обычными полосами. Вышеупомянутые символы ${ displaystyle D}$ , ${ displaystyle R}$ и ${ displaystyle L}$ исходят, конечно, из основной теории полугрупп.^[3]^[4]^[5]^[6]^[7]^[8]^[9]^[10]

Подмногообразия косых решеток

Косые решетки образуют множество. Прямоугольные косые решетки, левые и правые косые решетки образуют подмногообразия, которые являются центральными для базовой структурной теории косых решеток. Вот еще несколько.

Симметричные косые решетки

Косая решетка S симметрична, если для любого ${ displaystyle x, y in S}$ , ${ Displaystyle х клин у = у клин х}$ если ${ Displaystyle х ви у = у ви х}$ . Таким образом, вхождения коммутации однозначно для таких косых решеток, в которых подмножества попарно коммутирующих элементов порождают коммутативные подалгебры, т. Е. Подрешетки. (Это неверно для косых решеток в целом.) Базисы уравнений для этого подмногообразия, впервые данные Спинксом^[11] находятся: ${ Displaystyle х ви у ви (х клин у) = (у клин х) ви у ви х}$ и ${ Displaystyle х клин у клин (х ви у) = (у ви х) клин у клин х}$ .A секция решетки косой решетки ${ displaystyle S}$ это подрешетка ${ displaystyle T}$ из ${ displaystyle S}$ встреча каждого ${ displaystyle D}$ -класс ${ displaystyle S}$ в одном элементе. ${ displaystyle T}$ таким образом, является внутренней копией решетки ${ Displaystyle S / D}$ с составом ${ Displaystyle T подмножество S rightarrow S / D}$ являясь изоморфизмом. Все симметричные косые решетки, для которых | S / D | leq aleph_0, допускает секцию решетки.^[10] Симметричная или нет, имеющая решетчатый участок ${ displaystyle T}$ гарантирует, что ${ displaystyle S}$ также есть внутренние копии ${ displaystyle S / L}$ и ${ Displaystyle S / R}$ дано соответственно ${ displaystyle T [R] = bigcup _ {t in T} R_ {t}}$ и ${ displaystyle T [L] = bigcup _ {t in T} L_ {t}}$ , куда ${ displaystyle R_ {t}}$ и ${ displaystyle Lt}$ являются ${ displaystyle R}$ и ${ displaystyle L}$ классы конгруэнтности ${ displaystyle t}$ в ${ displaystyle T}$ . Таким образом ${ Displaystyle Т [R] подмножество S rightarrow S / L}$ и ${ Displaystyle Т [L] подмножество S rightarrow S / R}$ являются изоморфизмами.^[8] Это приводит к коммутирующей диаграмме вложения, дуализирующей предыдущую диаграмму Кимуры.

Решетки противодействия перекосу

Косая решетка сокращается, если ${ Displaystyle х vee y = x vee z}$ и ${ Displaystyle х клин у = х клин г}$ подразумевает ${ displaystyle y = z}$ и аналогично ${ Displaystyle х vee z = y vee z}$ и ${ Displaystyle х клин z = y клин z}$ подразумевает ${ displaystyle x = y}$ . Косые решетки с сокращением симметричны, и можно показать, что они образуют множество. В отличие от решеток они не обязательно должны быть распределительными, и наоборот.

Распределительные перекосы

Распределительные косые решетки определяются тождествами: ${ Displaystyle х клин (у ви г) клин х = (х клин у клин х) ви (х клин г клин х)}$ (D1) ${ Displaystyle х ви (у клин г) ви х = (х ви у ви х) клин (х ви г ви х).}$ (D'1)

В отличие от решеток (D1) и (D'1) в общем случае не эквивалентны для косых решеток, но они эквивалентны для симметричных косых решеток.^[9]^[12]^[13] Условие (D1) можно усилить до ${ Displaystyle х клин (y vee z) клин w = (x клин y клин w) vee (x клин z клин w)}$ (D2) в этом случае (D'1) является следствием. Косая решетка ${ displaystyle S}$ удовлетворяет как (D2), так и двойственному ему, ${ Displaystyle х ви (у клин г) ви ш = (х ви у ви ш) клин (х ви г ви ш)}$ , тогда и только тогда, когда он факторизуется как произведение дистрибутивной решетки и прямоугольной косой решетки. В последнем случае (D2) можно усилить до ${ Displaystyle х клин (у ви г) = (х клин у) ви (х клин г)}$ и ${ Displaystyle (y vee z) клин w = (y клин w) vee (z клин w)}$ . (D3) Сам по себе (D3) эквивалентен (D2) при добавлении симметрии.^[3] Таким образом, мы имеем шесть подмногообразий косых решеток, определяемых соответственно (D1), (D2), (D3) и их двойниками.

Нормальные косые решетки

Как видно выше, ${ Displaystyle клин}$ и ${ displaystyle vee}$ удовлетворить личность ${ displaystyle xyxzx = xyzx}$ . Полосы, удовлетворяющие более сильную идентичность, ${ displaystyle xyzx = xzyx}$ , называются нормальными. Косая решетка называется нормальной косой, если она удовлетворяет

${ Displaystyle x клин y клин z клин x = x клин z клин y клин x. (N)}$

Для каждого элемента a в нормальной косой решетке ${ displaystyle S}$ , набор ${ Displaystyle а клин S клин а}$ определяется { ${ Displaystyle а клин х клин а | х в S}$ } или эквивалентно { ${ Displaystyle х в S | х leq a}$ } является подрешеткой в ${ displaystyle S}$ , и наоборот. (Таким образом, нормальные косые решетки также называются локальными решетками.) Когда обе ${ Displaystyle клин}$ и ${ displaystyle vee}$ нормальные, ${ displaystyle S}$ изоморфно распадается на продукт ${ Displaystyle Т раз D}$ решетки ${ displaystyle T}$ и прямоугольная косая решетка ${ displaystyle D}$ , и наоборот. Таким образом, как нормальные косые решетки, так и расщепленные косые решетки образуют многообразия. Возвращаясь к распространению, ${ Displaystyle (D2) = (D1) + (N)}$ так что ${ displaystyle (D2)}$ характеризует разнообразие дистрибутивных нормальных косых решеток, а (D3) характеризует множество симметричных, дистрибутивных нормальных косых решеток.

Категориальные косые решетки

Косая решетка категорична, если непустые композиции биекций смежных классов являются биекциями смежных классов. Категориальные косые решетки образуют множество. Косые решетки в кольцах и нормальные косые решетки являются примерами алгебр на этом многообразии.^[4] Позволять ${ displaystyle a> b> c}$ с ${ displaystyle a in A}$ , ${ displaystyle b in B}$ и ${ displaystyle c in C}$ , ${ displaystyle varphi}$ быть смежной биекцией из ${ displaystyle A}$ к ${ displaystyle B}$ принимая ${ displaystyle a}$ к ${ displaystyle b}$ , ${ displaystyle psi}$ быть биекцией смежного класса из ${ displaystyle B}$ к ${ displaystyle C}$ принимая ${ displaystyle b}$ к ${ displaystyle c}$ и наконец ${ displaystyle chi}$ быть смежной биекцией из ${ displaystyle A}$ к ${ displaystyle C}$ принимая ${ displaystyle a}$ к ${ displaystyle c}$ . Косая решетка ${ displaystyle S}$ категоричен, если всегда выполняется равенство ${ displaystyle psi circ varphi = chi}$ , т.е. если составная частичная биекция ${ displaystyle psi circ varphi}$ если непустой - биекция смежного класса из ${ displaystyle C}$ -косет ${ displaystyle A}$ для ${ displaystyle A}$ -cosetof ${ displaystyle C}$ . То есть ${ Displaystyle (A клин b клин A) cap (C vee b vee C) = (C vee a vee C) клин b клин (C vee a vee C) = (A клин c клин A) vee b vee (A клин c клин A)}$ .Все дистрибутивные косые решетки категоричны. Хотя симметричные косые решетки могут и не быть. В некотором смысле они обнаруживают независимость между свойствами симметрии и дистрибутивности.^[3]^[4]^[6]^[9]^[10]^[11]^[13]^[14]

Косые булевы алгебры

Нулевым элементом в косой решетке S называется такой элемент 0 из S, что для всех ${ Displaystyle х в S,}$ ${ Displaystyle 0 клин х = 0 = х клин 0}$ или, вдвойне, ${ displaystyle 0 vee x = x = x vee 0.}$ (0)

Булева косая решетка - это симметричная дистрибутивная нормальная косая решетка с 0, ${ Displaystyle (S; vee, клин, 0),}$ такой, что ${ Displaystyle а клин S клин а}$ является булевой решеткой для каждого ${ displaystyle a in S.}$ Для такой косой решетки S разностный оператор определяется как x y = ${ Displaystyle х-х клин у клин х}$ где последний вычисляется в булевой решетке ${ Displaystyle х клин S клин х.}$ ^[1] При наличии (D3) и (0) характеризуется тождествами: ${ Displaystyle у клин х / у = 0 = х / у клин у}$ и ${ Displaystyle (х клин у клин х) ви х / у = х = х / у ви (х клин у клин х).}$ (S B) Таким образом, имеется множество косых булевых алгебр ${ Displaystyle (S; vee, клин, /, 0)}$ характеризуется тождествами (D3), (0) и (S B). Примитивная косая булева алгебра состоит из 0 и одного отличного от 0 D-класса. Таким образом, это результат присоединения 0 к прямоугольной косой решетке D через (0) с ${ Displaystyle х / у = х}$ , если ${ displaystyle y = 0}$ и ${ displaystyle 0}$ иначе. Каждая косая булева алгебра является подпрямым произведением примитивных алгебр. Косые булевы алгебры играют важную роль в изучении дискриминаторных многообразий и других обобщений универсальной алгебры булевого поведения.^[15]^[16]^[17]^[18]^[19]^[20]^[21]^[22]^[23]^[24]^[25]

Перекос решеток в кольца

Позволять ${ displaystyle A}$ быть звенеть и разреши ${ displaystyle E (A)}$ обозначить набор из всех Идемпотенты в ${ displaystyle A}$ . Для всех ${ displaystyle x, y in A}$ набор ${ Displaystyle х клин у = ху}$ и ${ Displaystyle х ви у = х + у-ху}$ .

Четко ${ Displaystyle клин}$ но также ${ displaystyle vee}$ является ассоциативный. Если подмножество ${ Displaystyle S substeq E (A)}$ закрыт под ${ Displaystyle клин}$ и ${ displaystyle vee}$ , тогда ${ Displaystyle (S, клин, vee)}$ является распределительной косой решеткой с сокращением. Чтобы найти такие косые решетки в ${ displaystyle E (A)}$ каждый смотрит на группы в ${ displaystyle E (A)}$ , особенно те, которые максимальны относительно некоторого ограничения. Фактически, каждая мультипликативная полоса в ${ displaystyle ()}$ который является максимальным относительно правильной регулярности (=), также замкнут относительно ${ displaystyle vee}$ и таким образом образует правую косую решетку. В общем, каждая правильная регулярная группа в ${ displaystyle E (A)}$ порождает правую косую решетку в ${ displaystyle E (A)}$ . Двойные замечания справедливы и для левых регулярных полос (полос, удовлетворяющих тождеству ${ displaystyle xyx = xy}$ ) в ${ displaystyle E (A)}$ . Максимальные регулярные полосы не нужно закрывать под ${ displaystyle vee}$ как определено; контрпримеры легко найти с помощью мультипликативных прямоугольных полос. Однако эти случаи закрыты кубическим вариантом ${ displaystyle vee}$ определяется ${ Displaystyle х набла у = х + у + yx-xyx-yxy}$ поскольку в этих случаях ${ Displaystyle х набла у}$ сводится к ${ displaystyle yx}$ чтобы дать двойную прямоугольную ленту. Заменив условие регулярности нормальностью ${ Displaystyle (xyzw = xzyw)}$ , каждая максимальная нормальная мультипликативная лента ${ displaystyle S}$ в ${ displaystyle E (A)}$ также закрыт ${ displaystyle nabla}$ с ${ Displaystyle (S; клин, vee, /, 0)}$ , куда ${ displaystyle x / y = x-xyx}$ , образует булеву косую решетку. Когда ${ displaystyle E (A)}$ сам замкнут относительно умножения, то это нормальная лента и, таким образом, образует булеву косую решетку. Фактически, любая косая булева алгебра может быть вложена в такую алгебру.^[26] Когда A имеет мультипликативную идентичность ${ displaystyle 1}$ , условие, что ${ displaystyle E (A)}$ мультипликативно замкнуто, как хорошо известно, следует, что ${ displaystyle E (A)}$ образует булеву алгебру. Косые решетки в кольцах по-прежнему служат хорошим источником примеров и мотивации.^[23]^[27]^[28]^[29]^[30]

Примитивные косые решетки

Косые решетки, состоящие ровно из двух D-классов, называются примитивными косыми решетками. Учитывая такую косую решетку ${ displaystyle S}$ с ${ displaystyle D}$ -классы ${ displaystyle A> B}$ в ${ Displaystyle S / D}$ , то для любого ${ displaystyle a in A}$ и ${ displaystyle b in B}$ , подмножества

${ Displaystyle А клин б клин А =}$ { ${ Displaystyle и клин Ь клин и: и в А}$ } ${ displaystyle substeq B}$ и ${ displaystyle B vee a vee B =}$ { ${ displaystyle v vee a vee v: v in B}$ } ${ displaystyle substeq A}$

называются соответственно смежные классы A в B и смежные классы B в A. Эти смежные классы разбивают B и A с ${ Displaystyle б в А клин б клин А}$ и ${ Displaystyle а ин В клин а клин В}$ . Классы смежных классов всегда являются прямоугольными подалгебрами в своих ${ displaystyle D}$ -классы. Более того, частичный порядок ${ displaystyle geq}$ индуцирует смежную биекцию ${ displaystyle varphi: B vee a vee B rightarrow A клин b клин A}$ определяется:

${ Displaystyle фи (х) = у}$ если только ${ displaystyle x> y}$ , за ${ displaystyle x in B vee a vee B}$ и ${ Displaystyle у в А клин б клин А}$ .

В совокупности смежные биекции описывают ${ displaystyle geq}$ между подмножествами ${ displaystyle A}$ и ${ displaystyle B}$ . Они также определяют ${ displaystyle vee}$ и ${ Displaystyle клин}$ для пар элементов из различных ${ displaystyle D}$ -классы. Действительно, учитывая ${ displaystyle a in A}$ и ${ displaystyle b in B}$ , позволять ${ displaystyle varphi}$ быть взаимно однозначным соотношением затрат между смежными классами ${ displaystyle B vee a vee B}$ в ${ displaystyle A}$ и ${ Displaystyle А клин б клин А}$ в ${ displaystyle B}$ . Потом:

${ displaystyle a vee b = a vee varphi -1 (b), b vee a = varphi -1 (b) vee a}$ и ${ Displaystyle а клин b = varphi (а) клин b, b клин а = b клин varphi (а)}$ .

В общем, учитывая ${ displaystyle a, c in A}$ и ${ displaystyle b, d in B}$ с ${ displaystyle a> b}$ и ${ displaystyle c> d}$ , тогда ${ displaystyle a, c}$ принадлежат к общему ${ displaystyle B}$ - сосет в ${ displaystyle A}$ и ${ displaystyle b, d}$ принадлежат к общему ${ displaystyle A}$ -косет в ${ displaystyle B}$ если и только если ${ displaystyle a> b // c> d}$ . Таким образом, каждая биекция смежных классов в некотором смысле является максимальным набором взаимно параллельных пар ${ displaystyle a> b}$ .

Каждая примитивная косая решетка ${ displaystyle S}$ факторов как расслоенное произведение его максимальных левых и правых примитивных изображений ${ Displaystyle S / R times _ {2} S / L}$ . Правые примитивные косые решетки строятся следующим образом. Позволять ${ Displaystyle A = чашка _ {i} A_ {i}}$ и ${ Displaystyle B = чашка _ {j} B_ {j}}$ быть разбиениями непересекающихся непустых множеств ${ displaystyle A}$ и ${ displaystyle B}$ , где все ${ displaystyle A_ {i}}$ и ${ displaystyle B_ {j}}$ имеют общий размер. Для каждой пары ${ displaystyle i, j}$ выбрать фиксированную биекцию ${ displaystyle varphi _ {i}, j}$ из ${ displaystyle A_ {i}}$ на ${ displaystyle B_ {j}}$ . На ${ displaystyle A}$ и ${ displaystyle B}$ отдельно установить ${ Displaystyle х клин у = у}$ и ${ Displaystyle х ви у = х}$ ; но учитывая ${ displaystyle a in A}$ и ${ displaystyle b in B}$ , набор

${ displaystyle a vee b = a, b vee a = a ', a wedge b = b}$ и ${ Displaystyle б клин а = б '}$

куда ${ Displaystyle varphi _ {я, j} (а ') = б}$ и ${ Displaystyle varphi _ {я, j} (а) = b '}$ с ${ displaystyle a '}$ принадлежащий ячейке ${ displaystyle A_ {i}}$ из ${ displaystyle a}$ и ${ displaystyle b '}$ принадлежащий ячейке ${ displaystyle B_ {j}}$ из ${ displaystyle b}$ . Различные ${ displaystyle varphi i, j}$ являются смежными биекциями. Это показано на следующей частичной диаграмме Хассе, где ${ displaystyle | A_ {i} | = | B_ {j} | = 2}$ а стрелки указывают ${ displaystyle varphi _ {я, j}}$ -выводы и ${ displaystyle geq}$ из ${ displaystyle A}$ и ${ displaystyle B}$ .

Левые примитивные косые решетки строятся двойственным образом. Таким способом могут быть построены все правые [левые] примитивные косые решетки.^[3]

Структура смежных классов косых решеток

Непрямоугольная косая решетка ${ displaystyle S}$ покрывается его максимальными примитивными косыми решетками: при сопоставимых ${ displaystyle D}$ -классы ${ displaystyle A> B}$ в ${ Displaystyle S / D}$ , ${ Displaystyle A чашка B}$ образует максимальную примитивную подалгебру в ${ displaystyle S}$ и каждый ${ displaystyle D}$ -класс в ${ displaystyle S}$ лежит в такой подалгебре. Структуры смежных классов этих примитивных подалгебр объединяются для определения результатов. ${ displaystyle x vee y}$ и ${ Displaystyle х клин у}$ по крайней мере, когда ${ displaystyle x}$ и ${ displaystyle y}$ сопоставимы под ${ displaystyle prevq}$ . Оказывается, что ${ displaystyle x vee y}$ и ${ Displaystyle х клин у}$ определяются в целом смежными классами и их биекциями, хотя и несколько менее прямым образом, чем ${ displaystyle prevq}$ -сравненный случай. В частности, даны два несравнимых D-класса A и B с объединенным D-классом J и встречающиеся с D-классом ${ displaystyle M}$ в ${ Displaystyle S / D}$ , возникают интересные связи между двумя смежными разложениями J (или M) по A и B.^[4]

Таким образом, косую решетку можно рассматривать как атлас смежных классов прямоугольных косых решеток, размещенных на вершинах решетки и взаимно однозначных смежных классов между ними, причем последние рассматриваются как частичные изоморфизмы между прямоугольными алгебрами, причем каждая биекция смежных классов определяет соответствующую пару смежных классов. Эта перспектива дает, по сути, диаграмму Хассе косой решетки, которую легко нарисовать в случаях относительно небольшого порядка. (См. Диаграммы в разделе 3 выше.) Дана цепочка D-классов ${ displaystyle A> B> C}$ в ${ Displaystyle S / D}$ , существует три набора биекций смежных классов: от A к B, от B к C и от A к C. ${ displaystyle varphi: A rightarrow B}$ и ${ displaystyle psi: B rightarrow C}$ , состав частичных биекций ${ displaystyle psi varphi}$ может быть пустым. Если это не так, то уникальная биекция смежного класса ${ displaystyle chi: A rightarrow C}$ существует такое, что ${ displaystyle psi varphi substeq chi}$ . (Опять таки, ${ displaystyle chi}$ является биекцией между парой смежных классов в ${ displaystyle A}$ и ${ displaystyle C}$ .) Это включение может быть строгим. Это всегда равенство (учитывая ${ displaystyle psi varphi neq emptyset}$ ) на данной косой решетке S в точности тогда, когда S категорична. В этом случае, путем включения тождественных отображений в каждый прямоугольный D-класс и присоединения пустых биекций между должным образом сопоставимыми D-классами, можно получить категорию прямоугольных алгебр и смежных биекций между ними. Простые примеры из раздела 3 категоричны.