Элементарная математика - Elementary mathematics

Коллекция геометрических формы. Все формы данного цвета похожий друг другу. Формы и базовая геометрия - важные темы элементарной математики.

Обе группы равны 5. Яблоки часто используются для объяснения арифметики в учебниках для детей.^[1]

Элементарная математика состоит из математика темы, часто преподаваемые в начальный или же Средняя школа уровни.

В учебной программе Канады есть шесть основных направлений элементарной математики: число, алгебра, данные, пространственное восприятие, финансовая грамотность, а также социальные эмоциональные навыки обучения и математические процессы. Эти шесть направлений составляют основу математического образования с 1 по 8 класс.^[2]

В средней школе основными предметами элементарной математики с девятого по десятый класс являются: чувство числа и алгебра, линейные отношения, измерение и геометрия.^[3] После того, как ученики поступают в одиннадцатый и двенадцатый классы, они начинают занятия по подготовке к университету и колледжу, которые включают: функции, исчисление и векторы, расширенные функции и управление данными.^[4]

Направления элементарной математики

Смысл чисел и нумерация

Number Sense - это понимание чисел и операций. В области определения чисел и нумерации учащиеся развивают понимание чисел, обучаясь различным способам представления чисел, а также отношениям между числами.^[5]

Свойства натуральные числа Такие как делимость и распределение простые числа, изучаются в базовых теория чисел, другая часть элементарной математики.

Элементарный фокус

Дроби и десятичные знаки
Место значение
Сложение и вычитание
Умножение и деление
Подсчет денег
Подсчет
Алгебра
Представляющие и заказные номера
Оценка
Решение проблем

Чтобы иметь прочную основу в математике и преуспевать в других областях, учащиеся должны иметь фундаментальные представления о смысле чисел и счислении.

Пространственное чувство

Навыки и концепции измерения или пространственное восприятие напрямую связаны с миром, в котором живут студенты. Многие концепции, которым обучают студентов в этом направлении, также используются в других предметах, таких как наука, общественные науки и физическое воспитание.^[6] В области измерения студенты узнают об измеряемых атрибутах объектов в дополнение к базовой метрической системе.

Элементарный фокус

Стандартные и нестандартные единицы измерения
определение времени в 12-часовом и 24-часовом формате
сравнение объектов с использованием измеримых атрибутов
измерение высоты, длины, ширины
сантиметры и метры
масса и вместимость
изменение температуры
дни, месяцы, недели, годы
расстояния в километрах
измерение килограммов и литров
определение площади и периметра
определение граммов и миллилитров
определение измерений с использованием таких форм, как треугольная призма

Нить измерения состоит из нескольких форм измерения, как утверждает Мэриан Смолл: «Измерение - это процесс присвоения качественного или количественного описания размера объекту на основе определенного атрибута».^[7]

Уравнения и формулы

Формула - это объект, построенный с использованием символов и правил формирования данного логический язык.^[8] Например, определение объем из сфера требует значительного количества интегральное исчисление или его геометрический аналог метод истощения;^[9] но, сделав это один раз с точки зрения некоторых параметр (в радиус например), математики создали формулу для описания объема: Эта конкретная формула:

V = 4 / 3 π р 3

Уравнение - это формула формы А = B, куда А и B находятся выражения который может содержать один или несколько переменные называется неизвестные, а "=" обозначает равенство бинарное отношение. Хотя написано в виде предложение, уравнение не является утверждение это либо истина, либо ложь, но проблема, состоящая в нахождении значений, называется решения, которые при замене неизвестных дают равные значения выражений А и B. Например, 2 - уникальный решение из уравнение Икс + 2 = 4, в котором неизвестный является Икс.^[10]

Данные

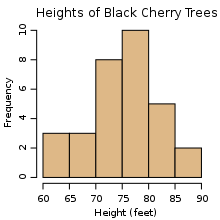
Пример гистограмма высотой 31 Черная вишня деревья. Гистограммы - это распространенный инструмент, используемый для представления данных.

Данные - это набор из значения из качественный или же количественный переменные; пересчитано, части данных являются отдельными частями Информация. Данные в вычисление (или же обработка данных ) представлена в структура это часто табличный (представлена ряды и столбцы ), а дерево (а набор из узлы с родитель -дети отношение ) или график (набор связаны узлы). Данные обычно являются результатом измерения и может быть визуализированный с помощью графики или же изображений.

Данные как Абстрактные концепция можно рассматривать как самый низкий уровень абстракция, откуда Информация а потом знание получены.

Базовая двухмерная геометрия

Двумерная геометрия - это ветвь математика занимается вопросами формы, размера и взаимного расположения двухмерных фигур. Основные темы элементарной математики включают многоугольники, круги, периметр и площадь.

А многоугольник что ограничено конечной цепочкой прямых отрезки линии замкнувшись в петлю, чтобы сформировать замкнутая цепочка или же схема. Эти сегменты называются его края или же стороны, а точки пересечения двух ребер - это точки многоугольника. вершины (единственное число: вершина) или углы. Внутреннюю часть многоугольника иногда называют его тело. An п-угольник многоугольник с п стороны. Многоугольник - это двумерный пример более общего многогранник в любом количестве измерений.

А круг это простой форма из двумерная геометрия это набор всех точки в самолет которые находятся на заданном расстоянии от заданной точки, центр Расстояние между любой из точек и центром называется радиус. Его также можно определить как геометрическое место точки, равноудаленной от фиксированной точки.

А периметр это путь, окружающий двумерный форма. Этот термин может использоваться либо для обозначения пути, либо для его длины - его можно рассматривать как длину контура фигуры. Периметр круг или же эллипс называется его длина окружности.

Площадь это количество что выражает степень двумерный фигура или форма. Есть несколько известных формулы для областей простых форм, таких как треугольники, прямоугольники, и круги.

Пропорции

Две величины пропорциональны, если изменение одной всегда сопровождается изменением другой, и если изменения всегда связаны с помощью постоянного множителя. Константа называется коэффициент соразмерности или константа пропорциональности.

Если одно количество всегда продукт другого и константы, эти два называются прямо пропорциональный. Икс и у прямо пропорциональны, если соотношение ${ displaystyle { tfrac {y} {x}}}$ постоянно.
Если произведение двух величин всегда равно константе, они называются обратно пропорциональный. Икс и у обратно пропорциональны, если произведение ${ displaystyle xy}$ постоянно.

Аналитическая геометрия

Декартовы координаты

Аналитическая геометрия это изучение геометрия используя система координат. Это контрастирует с синтетическая геометрия.

Обычно Декартова система координат применяется для управления уравнения за самолеты, прямые линии, и квадраты, часто в двух, а иногда и в трех измерениях. Геометрически изучается Евклидова плоскость (2 размера) и Евклидово пространство (3 измерения). Как учат в школьных учебниках, аналитическая геометрия может быть объяснена более просто: она связана с определением и представлением геометрических форм числовым способом и извлечением числовой информации из числовых определений и представлений форм.

Преобразования - это способы сдвига и масштабирования функций с использованием различных алгебраических формул.

Отрицательные числа

А отрицательное число это настоящий номер то есть меньше, чем нуль. Такие числа часто используются для обозначения суммы потери или отсутствия. Например, долг задолженность может рассматриваться как отрицательный актив, или уменьшение некоторого количества может рассматриваться как отрицательное увеличение. Отрицательные числа используются для описания значений по шкале ниже нуля, например Цельсия и Фаренгейт весы для температуры.

Экспоненты и радикалы

Возведение в степень - это математический операция, записанный как б^п, состоящий из двух чисел, основание б и показатель степени (или же мощность) п. Когда п это натуральное число (т.е. положительный целое число ) возведение в степень соответствует повторному умножение базы: то есть б^п это товар умножения п базы:

{ displaystyle b ^ {n} = underbrace {b times cdots times b} _ {n}}

Корни противоположны показателям. В n-й корень из номер Икс (написано ${ Displaystyle { sqrt [{п}] {х}}}$ ) это число р который при возведении к власти п даетИкс. То есть,

{ displaystyle { sqrt [{n}] {x}} = r iff r ^ {n} = x,}

куда п это степень корня. Корень степени 2 называется квадратный корень и корень степени 3, a кубический корень. Корни более высокой степени обозначаются порядковыми числами, как в четвертый корень, корень двадцатый, так далее.

Например:

2 - квадратный корень из 4, поскольку 2² = 4.
−2 также является квадратным корнем из 4, поскольку (−2)² = 4.

Циркуль и линейка

Циркуль и линейка, также известная как конструкция линейки и циркуля, представляет собой построение длин, углы, и другие геометрические фигуры, используя только идеализированный линейка и компас.

Идеализированный правитель, известный как прямая грань, предполагается бесконечной длины, без маркировки и только с одним краем. Предполагается, что компас схлопывается при поднятии со страницы, поэтому его нельзя напрямую использовать для переноса расстояний. (Это неважное ограничение, поскольку, используя многоступенчатую процедуру, расстояние можно передать даже с помощью сворачивающегося компаса, см. компас теорема эквивалентности.) Более формально, единственными допустимыми конструкциями являются те, которые предоставляются Евклид Первые три постулата.

Соответствие и сходство

Две фигуры или предметы являются конгруэнтными, если у них одинаковые форма и размер, или если один имеет ту же форму и размер, что и зеркальное отображение другого.^[11] Более формально, два набора точки называются конгруэнтный тогда и только тогда, когда одно может быть преобразовано в другое изометрия, т.е. комбинация жесткие движения, а именно перевод, а вращение, а отражение. Это означает, что любой объект можно перемещать и отражать (но не изменять размер) так, чтобы он точно совпадал с другим объектом. Таким образом, две отдельные плоские фигуры на листе бумаги являются конгруэнтными, если мы можем вырезать их, а затем полностью сопоставить. Переворачивание бумаги разрешено.

Два геометрических объекта называются похожий если у них обоих одинаковые форма, или один из них имеет ту же форму, что и зеркальное отражение другого. Точнее, одно можно получить из другого равномерно масштабирование (увеличение или уменьшение), возможно с дополнительными перевод, вращение и отражение. Это означает, что любой объект можно масштабировать, перемещать и отражать так, чтобы он точно совпадал с другим объектом. Если два объекта похожи, каждый конгруэнтный в результате равномерного масштабирования другого.

Трехмерная геометрия

Твердая геометрия было традиционным названием для геометрия трехмерного Евклидово пространство. Стереометрия имеет дело с измерения из тома различных твердые фигуры (трехмерный цифры) в том числе пирамиды, цилиндры, шишки, усеченные конусы, сферы, и призмы.

Рациональное число

Рациональное число есть ли номер что можно выразить как частное или дробь п/q из двух целые числа, с знаменатель q не равно нулю.^[12] С q может быть равно 1, каждое целое число является рациональным числом. В набор всех рациональных чисел обычно обозначается жирным шрифтом Q (или же классная доска жирным шрифтом ${ displaystyle mathbb {Q}}$ ).

Паттерны, отношения и функции

А шаблон является заметной закономерностью в мире или в искусственном замысле. Таким образом, элементы шаблона повторяются предсказуемым образом. А геометрический узор это своего рода узор, состоящий из геометрических фигур и обычно повторяющийся, как обои на стену.

А связь на набор А это собрание заказанные пары элементов А. Другими словами, это подмножество из Декартово произведение А² = А × А. Общие отношения включают делимость между двумя числами и неравенства.

А функция^[13] это связь между набор входов и набор допустимых выходов со свойством, что каждый вход связан ровно с одним выходом. Примером является функция, которая связывает каждое действительное число Икс на его площадь Икс². Выход функции ж соответствующий входу Икс обозначается ж(Икс) (читать "ж из Икс"). В этом примере, если вход равен −3, то выход равен 9, и мы можем написать ж(−3) = 9. Входные переменные иногда называют аргументами функции.

Склоны и тригонометрия

В наклон линии это число, которое описывает как направление и крутизна линии.^[14] Наклон часто обозначают буквой м.^[15]

Тригонометрия это филиал математика который изучает отношения, включающие длину и углы из треугольники. Это поле возникло в III веке до нашей эры в результате применения геометрия астрономическим исследованиям.^[16] Склон изучается в 8 классе.

Соединенные Штаты

в Соединенные Штаты, значительную озабоченность вызывает низкий уровень навыков элементарной математики у многих учащихся по сравнению с учащимися других развитых стран.^[17] В Ни один ребенок не остался позади Программа была одной из попыток устранить этот недостаток, требуя, чтобы все американские студенты проходили тестирование по элементарной математике.^[18]