Возведение в степень - Exponentiation

Графики у = б^Икс для различных баз б:   база 10,   базае,   база 2,   база1/2. Каждая кривая проходит через точку (0, 1) потому что любое ненулевое число, возведенное в степень 0, равно 1. При Икс = 1, значение у равно основанию, потому что любое число, возведенное в степень 1, и есть само число.

Арифметические операции

Дополнение (+) ${ displaystyle scriptstyle left. { begin {matrix} scriptstyle { text {term}} , + , { text {term}} scriptstyle { text {summand}} , + , { text {summand}} scriptstyle { text {addend (в широком смысле)}} , + , { text {addend (в широком смысле)}} scriptstyle { text {augend}} , + , { text {addend (в строгом смысле)}} end {matrix}} right } , = ,}$ ${ displaystyle scriptstyle { text {sum}}}$ Вычитание (−) ${ displaystyle scriptstyle left. { begin {matrix} scriptstyle { text {term}} , - , { text {term}} scriptstyle { text {minuend}} , - , { text {subtrahend}} end {matrix}} right } , = ,}$ ${ displaystyle scriptstyle { text {разница}}}$ Умножение (×) ${ displaystyle scriptstyle left. { begin {matrix} scriptstyle { text {factor}} , times , { text {factor}} scriptstyle { text {multiplier}} , раз , { text {multiplicand}} end {matrix}} right } , = ,}$ ${ displaystyle scriptstyle { text {product}}}$ Деление (÷) ${ displaystyle scriptstyle left. { begin {matrix} scriptstyle { frac { scriptstyle { text {divisor}}} { scriptstyle { text {divisor}}}} scriptstyle { text { }} scriptstyle { frac { scriptstyle { text {numerator}}} { scriptstyle { text {denominator}}}} end {matrix}} right } , = ,}$ ${ displaystyle { begin {matrix} scriptstyle { text {дробь}} scriptstyle { text {quotient}} scriptstyle { text {ratio}} end {matrix}}}$ Возведение в степень ${ displaystyle scriptstyle { text {base}} ^ { text {exponent}} , = ,}$ ${ displaystyle scriptstyle { text {power}}}$ пй корень (√) ${ displaystyle scriptstyle { sqrt [{ text {степень}}] { scriptstyle { text {radicand}}}} , = ,}$ ${ displaystyle scriptstyle { text {root}}}$ Логарифм (журнал) ${ Displaystyle scriptstyle log _ { text {base}} ({ text {антилогарифм}}) , = ,}$ ${ displaystyle scriptstyle { text {логарифм}}}$

Возведение в степень это математический операция, записанный как б^п, состоящий из двух чисел, база б и показатель степени или мощность п, и произносится как "б возведен во власть п".^[1][2] Когда п положительный целое число, возведение в степень соответствует повторному умножение базы: то есть б^п это товар умножения п базы:^[2]

${ displaystyle b ^ {n} = underbrace {b times dots times b} _ {n , { textrm {times}}}.}$

Показатель обычно показывают как надстрочный индекс справа от основания. В этом случае, б^п называется "b в степени n", "b в степени n",^[1] "n-я степень числа b", "b в n-й степени",^[3] или короче как «от б до н-го».

Надо б¹ = б, и для любых натуральных чисел м и п, надо б^п ⋅ б^м = б^п+м. Чтобы распространить это свойство на неположительные целые показатели, б⁰ определяется как 1, и б^−п (с участием п положительное целое число и б не ноль) определяется как 1/б^п. Особенно, б⁻¹ равно 1/б, то взаимный из б.

Определение возведения в степень может быть расширено, чтобы разрешить любые реальные или сложный экспонента. Возведение в степень целочисленными показателями также может быть определено для широкого спектра алгебраических структур, включая матрицы.

Возведение в степень широко используется во многих областях, в том числе экономика, биология, химия, физика, и Информатика, с такими приложениями, как сложные проценты, рост населения, кинетика химической реакции, волна поведение и криптография с открытым ключом.

История обозначения

Период, термин мощность (латинский: потенция, потестас, dignitas) является неправильным переводом^[4][5] из древнегреческий δύναμις (дунамис, здесь: "усиление"^[4]) используется Греческий математик Евклид для квадрата линии,^[6] следующий Гиппократ Хиосский.^[7] Архимед открыл и доказал закон экспонент, 10^а ⋅ 10^б = 10^а+б, необходимо манипулировать полномочиями 10.^{[8][нужен лучший источник ]} В IX веке персидский математик Мухаммад ибн Муса аль-Хваризми использовал термины مَال (мал, "имущество", "имущество") для квадрат - мусульмане, «как и большинство математиков того и более раннего времени, думали о квадрате числа как об изображении площади, особенно земли, а следовательно, и собственности».^[9]—И كَعْبَة (Kabah, «куб») для куб, который позже Исламский математики, представленные в математическая запись как буквы мим (м) и каф (k) соответственно к 15 веку, как видно из работы Абу аль-Хасан ибн Али аль-Каласади.^[10]

В конце 16 века Йост Бюрги использовали римские цифры для показателей.^[11]

Николя Шуке использовали форму экспоненциальной записи в 15 веке, которая позже была использована Хенрик Грамматеус и Майкл Стифель в 16 веке. Слово показатель степени был придуман в 1544 году Майклом Стифелем.^[12][13] Сэмюэл Джик ввел термин индексы в 1696 г.^[6] В 16 веке Роберт Рекорд использовали термины квадрат, куб, зензизензик (четвертая степень ), сурсоид (пятое), зензикубе (шестое), второе сурсолидное (седьмое) и зензизензизензик (восьмой).^[9] Биквадрат также использовалось для обозначения четвертой степени.

В начале 17 века первая форма нашей современной экспоненциальной записи была введена Рене Декарт в его тексте под названием La Géométrie; там обозначения вводятся в Книге I.^[14]

Некоторые математики (например, Исаак Ньютон ) использовали экспоненты только для степеней больше двух, предпочитая представлять квадраты как повторяющееся умножение. Таким образом они напишут многочлены, например, как топор + bxx + сх³ + d.

Еще один исторический синоним, инволюция, сейчас редко^[15] и не следует путать с его более общее значение.

В 1748 г. Леонард Эйлер написал:

"рассмотрим экспоненты или степени, в которых сама экспонента является переменной. Ясно, что такие величины не являются алгебраические функции, так как в них показатели должны быть постоянными ".^[16]

С этим введением трансцендентные функции, Эйлер заложил основы современного внедрения натуральный логарифм - как обратная функция для естественная экспоненциальная функция, ж(Икс) = е^Икс.

Терминология

Выражение б² = б ⋅ б называется " квадрат из б" или "б в квадрате », потому что площадь квадрата со стороной б является б².

Аналогично выражение б³ = б ⋅ б ⋅ б называется " куб из б" или "б в кубе ", потому что объем куба с длиной стороны б является б³.

Когда это положительное число, показатель степени указывает, сколько копий основания умножается. Например, 3⁵ = 3 ⋅ 3 ⋅ 3 ⋅ 3 ⋅ 3 = 243. База 3 появляется 5 раз в повторном умножении, потому что показатель степени равен 5. Вот, 243 это Пятая степень 3, или 3 в 5-й степени.

Слово «поднятый» обычно опускается, а иногда и слово «сила», поэтому 3⁵ можно просто читать «от 3 до 5» или «от 3 до 5». Следовательно, возведение в степень б^п можно выразить как "б к власти п", "б к пй степень ","б к пth ", или кратко как"б к п".

Целочисленные показатели

Операция возведения в степень с целыми показателями может быть определена непосредственно из элементарных арифметические операции.

Положительные показатели

Степени с положительными целыми показателями могут определяться базовым случаем.^[17]

${ displaystyle b ^ {1} = b}$

и отношение повторения

${ displaystyle b ^ {n + 1} = b ^ {n} cdot b.}$

В ассоциативность умножения означает, что для любых натуральных чисел м и п,

${ displaystyle b ^ {m + n} = b ^ {m} cdot b ^ {n}.}$

Нулевой показатель

Любое ненулевое число, возведенное в 0 сила 1:^[18][2]

${ displaystyle b ^ {0} = 1.}$

Одна интерпретация такой силы - как пустой продукт.

Случай 0⁰ является более сложным, и выбор того, назначать ли ему значение и какое значение назначать, может зависеть от контекста. Подробнее см. Ноль в степени нуля.

Отрицательные показатели

Следующее равенство выполняется для любого целого числа п и ненулевой б:

${ displaystyle b ^ {- n} = { frac {1} {b ^ {n}}}.}$^[2]

Возведение 0 в отрицательную экспоненту не определено, но в некоторых случаях это может быть интерпретировано как бесконечность (∞).

Приведенная выше идентичность может быть получена посредством определения, направленного на расширение диапазона показателей до отрицательных целых чисел.

Для ненулевого б и положительный п, приведенное выше рекуррентное соотношение можно переписать как

${ displaystyle b ^ {n} = { frac {b ^ {n + 1}} {b}}, quad n geq 1.}$

Определив это отношение как действительное для всех целых п и ненулевой б, это следует из того

${ displaystyle { begin {align} b ^ {0} & = { frac {b ^ {1}} {b}} = 1, [3pt] b ^ {- 1} & = { frac { b ^ {0}} {b}} = { frac {1} {b}}, end {align}}}$

и вообще для любого ненулевого б и любое неотрицательное целое число п,

${ displaystyle b ^ {- n} = { frac {1} {b ^ {n}}}.}$

Затем легко показать, что это верно для любого целого числа п.

Личности и свойства

Следующее идентичности выполняется для всех целочисленных показателей, при условии, что основание не равно нулю:^[2]

${ Displaystyle { begin {align} b ^ {m + n} & = b ^ {m} cdot b ^ {n} left (b ^ {m} right) ^ {n} & = b ^ {m cdot n} (b cdot c) ^ {n} & = b ^ {n} cdot c ^ {n} end {выровнено}}}$

В отличие от сложения и умножения:

Полномочия суммы

Степени суммы обычно вычисляются из степеней слагаемых биномиальная формула

${ displaystyle (a + b) ^ {n} = sum _ {i = 0} ^ {n} { binom {n} {i}} a ^ {i} b ^ {ni} = sum _ { i = 0} ^ {n} { frac {n!} {i! (ni)!}} a ^ {i} b ^ {ni}.}$

Однако эта формула верна, только если слагаемые коммутируют (т.е. ab = ба), что подразумевается, если они принадлежат структура это коммутативный. В противном случае, если а и б скажем, квадратные матрицы одинакового размера, эту формулу использовать нельзя. Отсюда следует, что в компьютерная алгебра, много алгоритмы с целыми показателями степени должны быть изменены, когда основания возведения в степень не коммутируются. Некоторая общая цель системы компьютерной алгебры используйте другие обозначения (иногда ^^ вместо того ^) для возведения в степень с некоммутирующими базисами, которое затем называется некоммутативное возведение в степень.

Комбинаторная интерпретация

Для неотрицательных целых чисел п и м, значение п^м это количество функции из набор из м элементы к набору п элементы (см. кардинальное возведение в степень ). Такие функции можно представить как м-кортежи из п-элементный набор (или как м-буквенные слова из п-буквенный алфавит). Некоторые примеры для конкретных значений м и п приведены в следующей таблице:

пм	В пм возможное м-наборы элементов из набора {1, ..., п}
${ displaystyle 0 ^ {5} = 0}$	никто
${ displaystyle 1 ^ {4} = 1}$	${ Displaystyle (1,1,1,1)}$
${ displaystyle 2 ^ {3} = 8}$	${ Displaystyle (1,1,1), (1,1,2), (1,2,1), (1,2,2), (2,1,1), (2,1,2) , (2,2,1), (2,2,2)}$
${ displaystyle 3 ^ {2} = 9}$	${ Displaystyle (1,1), (1,2), (1,3), (2,1), (2,2), (2,3), (3,1), (3,2) , (3,3)}$
${ displaystyle 4 ^ {1} = 4}$	${ Displaystyle (1), (2), (3), (4)}$
${ displaystyle 5 ^ {0} = 1}$	${ displaystyle ()}$

Особые базы

Степени десяти

В базе десятка (десятичная дробь ) система счисления, целые степени 10 записываются как цифра 1 за которым или перед ними стоит ряд нулей, определяемых знаком и величиной показателя степени. Например, 10³ = 1000 и 10⁻⁴ = 0.0001.

Возведение в степень с базой 10 используется в научная нотация для обозначения больших или маленьких чисел. Например, 299792458 РС (в скорость света в вакууме, в метров в секунду ) можно записать как 2.99792458×10⁸ РС а потом приблизительный так как 2.998×10⁸ РС.

Префиксы SI на основе полномочий 10 также используются для описания малых или больших количеств. Например, приставка килограмм означает 10³ = 1000, значит, километр 1000 м.

Полномочия двух

Первые отрицательные силы 2 широко используются и имеют специальные имена, например: половина и четверть.

Полномочия 2 появляться в теория множеств, так как набор с п члены имеют набор мощности, набор всех его подмножества, который имеет 2^п члены.

Целочисленные степени 2 важны в Информатика. Положительные целые степени 2^п укажите количество возможных значений для п-немного целое число двоичное число; например, байт может занять 2⁸ = 256 разные значения. В двоичная система счисления выражает любое число как сумму степеней 2, и обозначает ее как последовательность 0 и 1, разделенные двоичная точка, где 1 указывает на силу 2 что появляется в сумме; показатель степени определяется местом этого 1: неотрицательные показатели - это ранг 1 слева от точки (начиная с 0), а отрицательные показатели определяются рангом справа от точки.

Полномочия одного

Силы одного все едины: 1^п = 1.

Степень нуля

Если показатель степени п положительный (п > 0), п-я степень нуля равна нулю: 0^п = 0.

Если показатель степени п отрицательный (п < 0), п-я степень нуля 0^п не определено, поскольку должно быть равно ${ displaystyle 1/0 ^ {- n}}$ с участием -п > 0, и это будет ${ displaystyle 1/0}$ согласно выше.

Выражение 0⁰ либо определяется как 1, либо остается неопределенным (увидеть Ноль в степени нуля ).

Полномочия отрицательного

Если п - четное целое число, то (−1)^п = 1.

Если п - нечетное целое число, тогда (−1)^п = −1.

Из-за этого полномочия −1 полезны для выражения чередующихся последовательности. Для аналогичного обсуждения степеней комплексного числа я, увидеть § Степени комплексных чисел.

Большие показатели

В предел последовательности степеней числа больше единицы расходится; другими словами, последовательность неограниченно растет:

б^п → ∞ так как п → ∞ когда б > 1

Это можно прочитать как "б к власти п как правило +∞ так как п стремится к бесконечности, когда б больше единицы ".

Полномочия числа с абсолютная величина меньше единицы стремятся к нулю:

б^п → 0 так как п → ∞ когда |б| < 1

Любая сила единицы всегда одна:

б^п = 1 для всех п если б = 1

Полномочия –1 чередовать 1 и –1 так как п чередуется между четным и нечетным, и поэтому не стремится к какому-либо пределу, поскольку п растет.

Если б < –1, б^п, чередуется между большими и большими положительными и отрицательными числами как п чередуется между четным и нечетным, и поэтому не стремится к какому-либо пределу, поскольку п растет.

Если возведенное в степень число меняется, стремясь к 1 поскольку показатель степени стремится к бесконечности, то предел не обязательно является одним из указанных выше. Особенно важным случаем является

(1 + 1/п)^п → е так как п → ∞

Увидеть § Показательная функция ниже.

Другие ограничения, в частности те, которые имеют выражения, которые принимают неопределенная форма, описаны в § Пределы полномочий ниже.

Силовые функции

Силовые функции для ${ displaystyle n = 1,3,5}$

Силовые функции для ${ displaystyle n = 2,4,6}$

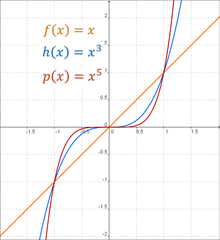
Реальные функции формы ${ displaystyle f (x) = cx ^ {n}}$, где ${ displaystyle c neq 0}$, иногда называют степенными функциями.^{[нужна цитата ]} Когда ${ displaystyle n}$ является целое число и ${ Displaystyle п geq 1}$, существует два основных семейства: для ${ displaystyle n}$ даже, и для ${ displaystyle n}$ странный. В общем для ${ displaystyle c> 0}$, когда ${ displaystyle n}$ даже ${ displaystyle f (x) = cx ^ {n}}$ будет иметь тенденцию к положительному бесконечность с увеличением ${ displaystyle x}$, а также в сторону положительной бесконечности с уменьшением ${ displaystyle x}$. Все графики из семейства четных степенных функций имеют общий вид ${ displaystyle y = cx ^ {2}}$, сглаживая больше посередине, как ${ displaystyle n}$ увеличивается.^[23] Функции с такими симметрия (${ Displaystyle f (-x) = f (x)}$) называются четные функции.

Когда ${ displaystyle n}$ странно, ${ displaystyle f (x)}$с асимптотический поведение меняется с положительного ${ displaystyle x}$ к отрицательному ${ displaystyle x}$. Для ${ displaystyle c> 0}$, ${ displaystyle f (x) = cx ^ {n}}$ также будет иметь тенденцию к положительному бесконечность с увеличением ${ displaystyle x}$, но в сторону отрицательной бесконечности с уменьшением ${ displaystyle x}$. Все графы из семейства нечетно-степенных функций имеют общий вид ${ displaystyle y = cx ^ {3}}$, сглаживая больше посередине, как ${ displaystyle n}$ возрастает и теряет всю плоскостность на прямой для ${ Displaystyle п = 1}$. Функции с такой симметрией (${ Displaystyle f (-x) = - f (x)}$) называются нечетные функции.

Для ${ displaystyle c <0}$, в каждом случае верна противоположная асимптотика.^[23]

Список целочисленных степеней

Рациональные показатели

Эта секция читается как учебник и может потребовать уборка. Пожалуйста помоги чтобы улучшить эту статью сделать это нейтральный в тон и познакомьтесь с Википедией стандарты качества. (Февраль 2020 г.)

Сверху вниз: Икс^1/8, Икс^1/4, Икс^1/2, Икс¹, Икс², Икс⁴, Икс⁸.

An пй корень из количество б это число Икс такой, что Икс^п = б.

Если б положительное действительное число и п является положительным целым числом, то существует ровно одно положительное вещественное решение Икс^п = б. Это решение называется главный пй корень из б. Обозначается ^п√б, где √   это радикальный символ; в качестве альтернативы главный корень может быть записан б^1/п. Например: 9^1/2 = √9 = 3 и 8^1/3 = ³√8 = 2.

Дело в том, что ${ Displaystyle х = Ь ^ { гидроразрыва {1} {п}}}$ решает ${ displaystyle x ^ {n} = b}$ следует из того, что

${ displaystyle { begin {align} x ^ {n} & = left (b ^ { frac {1} {n}} right) ^ {n} = underbrace {b ^ { frac {1} {n}} times b ^ { frac {1} {n}} times cdots times b ^ { frac {1} {n}}} _ {n , { textrm {times}}} & = b ^ { underbrace { left ({ frac {1} {n}} + { frac {1} {n}} + cdots + { frac {1} {n}} right )} _ {n , { textrm {times}}}} = b ^ { frac {n} {n}} = b ^ {1} = b. end {align}}}$

Если б равно 0, уравнение Икс^п = б имеет одно решение, которое Икс = 0.

Если п является даже и б положительно, то Икс^п = б имеет два реальных решения: положительное и отрицательное. пкорни б, это, б^1/п > 0 и −(б^1/п) < 0.

Если п даже и б отрицательно, уравнение не имеет решения в действительных числах.

Если п странно, то Икс^п = б имеет ровно одно действительное решение, которое положительно, если б положительный (б^1/п > 0) и отрицательное, если б отрицательный (б^1/п < 0).

Принимая положительное действительное число б к рациональный показатель степени ты/v, где ты целое число и v является положительным целым числом и, учитывая только главные корни, дает

${ displaystyle b ^ { frac {u} {v}} = left (b ^ {u} right) ^ { frac {1} {v}} = { sqrt [{v}] {b ^ {u}}} = left (b ^ { frac {1} {v}} right) ^ {u} = left ({ sqrt [{v}] {b}} right) ^ {u }.}$

Принимая отрицательное действительное число б к рациональной власти ты/v, где ты/v в самом низком выражении дает положительный реальный результат, если ты четно, и, следовательно, v странно, потому что тогда б^ты положительный; и дает отрицательный реальный результат, если ты и v оба нечетные, потому что тогда б^ты отрицательный. Случай даже v (и, следовательно, нечетное ты) нельзя рассматривать таким образом в вещественных числах, поскольку нет действительного числа Икс такой, что Икс^2k = −1, значение б^ты/v в этом случае необходимо использовать мнимая единица я, как более подробно описано в разделе § Степени комплексных чисел.

Таким образом, мы имеем (−27)^1/3 = −3 и (−27)^2/3 = 9. Число 4 имеет две степени 3/2, а именно 8 и −8; однако условно обозначение 4^3/2 нанимает главный корень, и приводит к 8. За использование v-й корень ты/v-я степень также называют v/ты-й корень и даже для v период, термин главный корень обозначает также положительный результат.

Эту двусмысленность знака необходимо учитывать при применении идентификаторов власти. Например:

${ displaystyle -27 = (- 27) ^ { left ( left ({ frac {2} {3}} right) left ({ frac {3} {2}} right) right) } = left ((- 27) ^ { frac {2} {3}} right) ^ { frac {3} {2}} = 9 ^ { frac {3} {2}} = 27}$

явно не так.Проблема начинается уже в первом равенстве, если ввести стандарт обозначение для неоднозначной по своей сути ситуации - запрос четного корня - и просто ошибочное полагание только на один, обычный или главный интерпретация. Та же проблема возникает и с неверно введенной замещающей нотацией, которая по своей сути обеспечивает положительный результат:

${ displaystyle left ((- 27) ^ { frac {2} {3}} right) ^ { frac {3} {2}} = { sqrt { left ({ sqrt [{3} ] {(- 27) ^ {2}}} right) ^ {3}}} = { sqrt {(-27) ^ {2}}} neq -27}$

вместо того

${ displaystyle left ((- 27) ^ { frac {2} {3}} right) ^ { frac {3} {2}} = - { sqrt { left ({ sqrt [{3 }] {(- 27) ^ {2}}} right) ^ {3}}} = - { sqrt {(-27) ^ {2}}} = - 27.}$

Как правило, для комплексных чисел возникают те же проблемы, что описаны в разделе § Отказ от тождества мощности и логарифма.

Реальные показатели

Возведение в степень действительных положительных действительных чисел может быть определено либо расширением рациональных степеней до действительных чисел по непрерывности, либо, как правило, как указано в § Полномочия через логарифмы ниже. Результатом всегда является положительное действительное число, а идентичности и свойства показанные выше для целочисленных показателей верны и для положительных вещественных оснований с нецелочисленными показателями.

С другой стороны, возведение в степень до действительной степени отрицательного действительного числа гораздо сложнее определить последовательно, поскольку оно может быть нереальным и иметь несколько значений (см. § Действительные показатели с отрицательной базой ). Можно выбрать одно из этих значений, называемое основная стоимость, но нет выбора главного значения, для которого идентичность, например

${ displaystyle left (b ^ {r} right) ^ {s} = b ^ {r cdot s}}$

правда; увидеть § Отказ от тождества мощности и логарифма. Следовательно, возведение в степень с базисом, не являющимся положительным действительным числом, обычно рассматривается как многозначная функция.

Пределы рациональных показателей

Поскольку экспонента непрерывна, мы находим ${ displaystyle lim _ {n to infty} e ^ {x_ {n}} = e ^ { lim _ {n to infty} x_ {n}}}$ для сходящихся последовательностей (Икс_п). Это показано здесь для Икс_п = 1/п.

Поскольку любой иррациональный номер можно выразить как предел последовательности рациональных чисел, возведение в степень положительного действительного числа б с произвольной действительной экспонентой Икс можно определить как непрерывность с правилом^[24]

${ displaystyle b ^ {x} = lim _ {r ( in mathbb {Q}) to x} b ^ {r} quad (b in mathbb {R} ^ {+}, , х in mathbb {R}),}$

где предел как р приближается к Икс берется только над рациональными значениями р. Этот предел существует только для положительных б. В (ε, δ) -определение лимита используется; это включает в себя демонстрацию того, что для любой желаемой точности результата б^Икс можно выбрать достаточно малый интервал вокруг Икс поэтому все рациональные степени в интервале находятся в пределах желаемой точности.

Например, если Икс = π, неопределенное десятичное представление π = 3.14159… может использоваться (исходя из строгой монотонности рациональной степени) для получения интервалов, ограниченных рациональными степенями

${ Displaystyle влево [Ь ^ {3}, Ь ^ {4} вправо]}$, ${ Displaystyle влево [Ь ^ {3.1}, Ь ^ {3.2} вправо]}$, ${ displaystyle left [b ^ {3.14}, b ^ {3.15} right]}$, ${ displaystyle left [b ^ {3.141}, b ^ {3.142} right]}$, ${ displaystyle left [b ^ {3.1415}, b ^ {3.1416} right]}$, ${ displaystyle left [b ^ {3.14159}, b ^ {3.14160} right]}$, ${ displaystyle ldots}$

Ограниченные интервалы сходятся к единственному действительному числу, обозначенному ${ displaystyle b ^ { pi}}$. Этот метод можно использовать для получения степени положительного действительного числа. б для любого иррационального показателя. Функция ж_б(Икс) = б^Икс таким образом определено для любого действительного числа Икс.

Экспоненциальная функция

Важная математическая константа е иногда называют Число Эйлера, примерно равна 2,718 и является основанием натуральный логарифм. Хотя возведение в степень е в принципе могут рассматриваться так же, как возведение в степень любого другого действительного числа, такие экспоненты обладают особенно элегантными и полезными свойствами. Среди прочего, эти свойства допускают экспоненты от е быть обобщенным естественным образом на другие типы показателей, такие как комплексные числа или даже матрицы, при этом совпадая со знакомым значением возведения в степень с рациональными показателями.

Как следствие, обозначения е^Икс обычно обозначает обобщенное определение возведения в степень, называемое экспоненциальная функция, ехр (Икс), который можно определить многими эквивалентными способами, например, по

${ displaystyle exp (x) = lim _ {n to infty} left (1 + { frac {x} {n}} right) ^ {n}.}$

Среди других свойств exp удовлетворяет экспоненциальному тождеству

${ Displaystyle ехр (х + Y) = ехр (х) CDOT ехр (у).}$

Экспоненциальная функция определена для всех целых, дробных, вещественных и сложный ценности Икс. Фактически, матричная экспонента хорошо определен для квадратные матрицы (в этом случае экспоненциальное тождество выполняется только тогда, когда Икс и у коммутируют) и полезен для решения систем линейные дифференциальные уравнения.

Поскольку exp (1) равно е, и exp (Икс) удовлетворяет этому экспоненциальному тождеству, немедленно следует, что exp (Икс) совпадает с определением многократного умножения е^Икс для целого числа Икс, а также следует, что рациональные степени обозначают (положительные) корни, как обычно, так что exp (Икс) совпадает с е^Икс определения в предыдущем разделе для всех реальных Икс по преемственности.

Полномочия через логарифмы

Когда е^Икс определяется как экспоненциальная функция, б^Икс можно определить, для других положительных действительных чисел б, с точки зрения е^Икс. В частности, натуральный логарифм ln (Икс) это обратный экспоненциальной функции е^Икс. Он определен для б > 0, и удовлетворяет

${ displaystyle b = e ^ { ln b}.}$

Если б^Икс состоит в том, чтобы сохранить правила логарифма и экспоненты, тогда нужно иметь

${ displaystyle b ^ {x} = left (e ^ { ln b} right) ^ {x} = e ^ {x cdot ln b}}$

для каждого действительного числа Икс.

Это может быть использовано как альтернативное определение степени действительного числа б^Икс и согласуется с определением, данным выше, используя рациональные показатели и непрерывность. Определение возведения в степень с использованием логарифмов чаще встречается в контексте комплексных чисел, как обсуждается ниже.

Реальные показатели с отрицательной базой

Степени положительного действительного числа всегда являются положительными действительными числами. Решение x² = 4, однако, может быть либо 2, либо −2. Главное значение 4^1/2 равно 2, но −2 также является правильным квадратным корнем. Если определение возведения в степень действительных чисел будет расширено, чтобы разрешить отрицательные результаты, то результат больше не будет корректным.

Ни метод логарифмирования, ни метод рациональной экспоненты не могут использоваться для определения б^р как действительное число для отрицательного действительного числа б и произвольное действительное число р. Действительно, е^р положительно для каждого действительного числа р, так что ln (б) не определяется как действительное число для б ≤ 0.

Метод рациональной экспоненты нельзя использовать для отрицательных значений б потому что он полагается на непрерывность. Функция ж(р) = б^р имеет уникальное непрерывное расширение^[24] от рациональных чисел к действительным числам для каждого б > 0. Но когда б < 0, функция ж не является даже непрерывным на множестве рациональных чисел р для которого он определен.

Например, рассмотрим б = −1. В п-й корень из −1 равен −1 для каждого нечетного натурального числа п. Так что если п нечетное положительное целое число, (−1)^(м/п) = −1 если м странно, и (−1)^(м/п) = 1 если м даже. Таким образом, множество рациональных чисел q для которого (−1)^q = 1 является плотный в рациональных числах, как и множество q для которого (−1)^q = −1. Это означает, что функция (−1)^q не является непрерывным ни при каком рациональном числе q где это определено.

С другой стороны, произвольные сложные полномочия отрицательных чисел б можно определить, выбрав сложный логарифм из б.

Иррациональные показатели

Если б положительный реальный алгебраическое число, и Икс - рациональное число, выше было показано, что б^Икс - алгебраическое число. Это остается верным, даже если принять любое алгебраическое число для б, с той лишь разницей, что б^Икс может принимать несколько значений (конечное число, см. ниже), которые все являются алгебраическими. Теорема Гельфонда – Шнайдера дает некоторую информацию о природе б^Икс когда Икс является иррациональный (это, не рационально). Говорится:

Если б - алгебраическое число, отличное от 0 и 1, и Икс иррациональное алгебраическое число, то все значения б^Икс (их бесконечно много) трансцендентный (то есть не алгебраический).

Комплексные показатели с положительной действительной базой

Если б положительное действительное число, и z есть ли комплексное число, сила б^z определяется

${ Displaystyle Ь ^ {z} = е ^ {(z ln b)},}$

где Икс = ln (б) единственное действительное решение уравнения е^Икс = б, и комплексная мощность е определяется экспоненциальная функция, что является уникальным функция комплексной переменной который равен своей производной и принимает значение 1 для Икс = 0.

Как, в общем, б^z не является действительным числом, выражение, такое как (б^z)^ш не определяется предыдущим определением. Это должно интерпретироваться с помощью правил для степени комплексных чисел, и, если только z реально или ш является целым числом, обычно не равно б^zw, как и следовало ожидать.

Есть разные определения экспоненциальной функции но они совместимо распространяются на комплексные числа и удовлетворяют экспоненциальному свойству. Для любых комплексных чисел z и ш, экспоненциальная функция удовлетворяет ${ displaystyle e ^ {z + w} = e ^ {z} e ^ {w}}$. В частности, для любого комплексного числа ${ displaystyle z = x + iy}$

${ displaystyle e ^ {z} = e ^ {x + iy} = e ^ {x} cdot e ^ {iy},}$

Второй срок ${ displaystyle e ^ {iy}}$ имеет значение, определяемое Формула Эйлера

${ displaystyle e ^ {iy} = cos y + i sin y.}$

Эта формула связывает проблемы в тригонометрия и алгебра.

Следовательно, для любого комплексного числа ${ displaystyle z = x + iy,}$

${ displaystyle e ^ {z} = e ^ {x + iy} = e ^ {x} cdot e ^ {iy} = e ^ {x} ( cos y + i sin y).}$

Из-за Пифагорейская тригонометрическая идентичность, то абсолютная величина из ${ Displaystyle соз у + я грех у}$ является 1. Следовательно, реальный фактор ${ displaystyle e ^ {x}}$ абсолютное значение ${ displaystyle e ^ {z}}$ и мнимая часть ${ displaystyle y}$ экспоненты определяет аргумент (угол) комплексного числа ${ displaystyle e ^ {z}}$.

Определение серии

Показательная функция равна своей производной и удовлетворяет ${ displaystyle e ^ {0} = 1,}$ его Серия Тейлор должно быть

${ displaystyle e ^ {z} = sum _ {n = 0} ^ { infty} {z ^ {n} over n!} = 1 + z + { frac {z ^ {2}} {2! }} + { frac {z ^ {3}} {3!}} + { frac {z ^ {4}} {4!}} + cdots.}$

Эта бесконечная серия, которое часто принимают за определение экспоненциальной функции е^z для произвольных комплексных показателей абсолютно сходящийся для всех комплексных чисел z.

Когда z чисто воображаемый, это, z = иу для реального числа у, приведенная выше серия становится

${ displaystyle e ^ {iy} = 1 + iy + { frac {(iy) ^ {2}} {2!}} + { frac {(iy) ^ {3}} {3!}} + { frac {(iy) ^ {4}} {4!}} + cdots,}$

который (поскольку он абсолютно сходится) может быть переупорядочен как

${ displaystyle e ^ {iy} = left (1 - { frac {y ^ {2}} {2!}} + { frac {y ^ {4}} {4!}} - { frac { y ^ {6}} {6!}} + cdots right) + i left (y - { frac {y ^ {3}} {3!}} + { frac {y ^ {5}}) {5!}} - cdots right).}$

Реальная и мнимая части этого выражения равны Разложения Тейлора косинуса и синуса соответственно, с центром в нуле, что подразумевает формулу Эйлера:

${ displaystyle e ^ {iy} = cos y + i sin y.}$

Определение предела

Эта анимация показывает многократное умножение в комплексная плоскость для ценностей п (обозначается как N на картинке), увеличиваясь от 1 к 100, Как ${ Displaystyle (1 + я пи / п) ^ {п}}$ подходы −1. Ценности ${ Displaystyle (1 + я пи / п) ^ {к},}$ для k = 0 ... п, являются вершинами многоугольного пути, крайний левый конец которого ${ Displaystyle (1 + я пи / к) ^ {к}}$ для фактического k. Видно, что как k становится больше ${ Displaystyle (1 + я пи / к) ^ {к}}$ приближается к пределу −1, иллюстрирующий Тождество Эйлера: ${ displaystyle e ^ {я pi} = - 1.}$

Другая характеристика экспоненциальной функции ${ displaystyle e ^ {z}}$ как предел из ${ Displaystyle (1 + г / п) ^ {п}}$, так как п приближается к бесконечности. Думая о п-я степень в этом определении как повторное умножение в полярная форма, его можно использовать для наглядной иллюстрации формулы Эйлера. Любое комплексное число можно представить в полярной форме как ${ Displaystyle (г, тета)}$, где р - абсолютное значение и θ это его аргумент. Произведение двух комплексных чисел ${ displaystyle (r_ {1}, theta _ {1})}$ и ${ displaystyle (r_ {2}, theta _ {2})}$ является ${ displaystyle (r_ {1} r_ {2}, theta _ {1} + theta _ {2})}$.

Рассмотрим прямоугольный треугольник в комплексная плоскость который имеет ${ displaystyle 0}$, ${ displaystyle 1}$, и ${ displaystyle 1 + ix / n}$ как вершины. Для больших значений п, треугольник почти круговой сектор с радиусом 1 и малым центральным углом, равным ${ Displaystyle х / п}$ радианы. 1 + ${ displaystyle ix / n}$ затем можно аппроксимировать числом в полярной форме ${ Displaystyle (1, х / п)}$. Итак, в пределе при п приближается к бесконечности, ${ displaystyle (1 + ix / n) ^ {n}}$ подходы ${ Displaystyle (1, х / п) ^ {п} = (1 ^ {п}, пх / п) = (1, х)}$, точка на единичный круг чей угол от положительная действительная ось является Икс радианы. В Декартовы координаты этого пункта ${ Displaystyle ( соз х, грех х)}$, так ${ Displaystyle е ^ {ix} = соз х + я грех х}$; это снова формула Эйлера, допускающая те же связи с тригонометрическими функциями, что и при определении ряда.

Периодичность

Решения уравнения ${ displaystyle e ^ {z} = 1}$ являются целыми числами, кратными ${ displaystyle 2 pi i}$:

${ displaystyle left {z: e ^ {z} = 1 right } = {2k pi i: k in mathbb {Z} }}$

Таким образом, если ${ displaystyle v}$ комплексное число такое, что ${ Displaystyle е ^ {v} = ш}$, то каждые ${ displaystyle z}$ это также удовлетворяет ${ displaystyle e ^ {z} = w}$ можно получить из ${ Displaystyle е ^ {z} = е ^ {v} cdot 1 = e ^ {v + i2k pi}}$, т.е. добавлением произвольного целого числа, кратного ${ displaystyle 2 pi i}$ к ${ displaystyle v}$:

${ displaystyle left {z: e ^ {z} = w right } = {v + 2k pi i: k in mathbb {Z} }}$

То есть комплексная экспоненциальная функция ${ Displaystyle е ^ {Z} = ехр (г) = ехр (г + 2к пи я)}$ для любого целого числа k это периодическая функция с периодом ${ displaystyle 2 pi i}$.

Примеры

${ displaystyle { begin {align} 2 ^ {i} & = e ^ {i ln (2)} = cos { big (} ln (2) { big)} + i sin { big (} ln (2) { big)} приблизительно 0,76924 + 0,63896i, e ^ {i} & = cos (1) + i sin (1) приблизительно 0,54030 + 0,84147i, left (e ^ {2 pi} right) ^ {i} & = e ^ {i ln (e ^ {2 pi})} = e ^ {i (2 pi)} = cos ( 2 pi) + i sin (2 pi) = 1. End {align}}}$

Степени комплексных чисел

Целочисленные степени ненулевых комплексных чисел определяются повторным умножением или делением, как указано выше. Если я это мнимая единица и п целое число, тогда я^п равно 1, я, −1 или -я, в зависимости от того, целое ли число п сравнимо с 0, 1, 2 или 3 по модулю 4. Из-за этого степени я полезны для выражения последовательности из период 4.

Сложные степени положительных вещественных чисел определяются через е^Икс как в разделе Комплексные показатели с положительным действительным основанием над. Это непрерывные функции.

Попытка распространить эти функции на общий случай нецелочисленных степеней комплексных чисел, не являющихся положительными действительными числами, приводит к трудностям. Либо мы определяем разрывные функции, либо многозначные функции. Ни один из этих вариантов не является полностью удовлетворительным.

Рациональная степень комплексного числа должна быть решением алгебраического уравнения. Следовательно, он всегда имеет конечное число возможных значений. Например, ш = z^1/2 должно быть решением уравнения ш² = z. Но если ш это решение, значит, так оно и есть -ш, потому что (−1)² = 1. Уникальное, но несколько произвольное решение, названное основная стоимость может быть выбран с использованием общего правила, которое также применимо к нерациональным полномочиям.

Комплексные степени и логарифмы более естественно обрабатывать как однозначные функции на Риманова поверхность. Однозначные версии определяются путем выбора листа. Значение имеет разрыв по срезанная ветка. Выбор одного из многих решений в качестве главного значения оставляет нам функции, которые не являются непрерывными, и обычные правила манипулирования полномочиями могут сбить нас с пути.

Любая нерациональная степень комплексного числа имеет бесконечное количество возможных значений из-за многозначной природы комплексный логарифм. Главное значение - это одно значение, выбранное из них правилом, которое, среди других свойств, гарантирует, что степени комплексных чисел с положительной действительной частью и нулевой мнимой частью дают то же значение, что и определенное правило над для соответствующей реальной базы.

Возведение действительного числа в степень в комплексной степени формально отличается от операции для соответствующего комплексного числа. Однако в общем случае положительного действительного числа главное значение то же самое.

Степени отрицательных действительных чисел не всегда определены и не являются непрерывными даже там, где они определены. Фактически, они определены только тогда, когда показатель степени является рациональным числом со знаменателем, являющимся нечетным целым числом. При работе с комплексными числами вместо этого обычно используется операция комплексного числа.

Сложные показатели со сложными основаниями

Для комплексных чисел ш и z с участием ш ≠ 0, обозначение ш^z неоднозначен в том же смысле, что журналш является.

Чтобы получить значение ш^z, сначала выберите логарифм ш; назови это журнал ш. Такой выбор может быть основная стоимость Журнал ш (значение по умолчанию, если не указано иное), или, возможно, значение, указанное каким-либо другим ветка журналаш фиксируется заранее. Затем, используя комплексную экспоненциальную функцию, определяют

${ Displaystyle ш ^ {г} = е ^ {г журнал ш}}$

потому что это согласуется с более раннее определение в случае, когда ш положительное действительное число и (реальное) главное значение журнал ш используется.

Если z является целое число, то значение ш^z не зависит от выбора журнал ш, и это согласуется с более раннее определение возведения в степень с целым показателем.

Если z это рациональное число м/п в самые низкие сроки с z > 0, то счетно бесконечно много вариантов журнал ш только уступать п разные значения для ш^z; эти значения являются п комплексные решения s к уравнению s^п = ш^м.

Если z является иррациональный номер, то счетно бесконечно много вариантов выбора журнал ш приводят к бесконечному множеству различных значений для ш^z.

Вычисление сложных степеней облегчается преобразованием базового ш к полярная форма, как подробно описано ниже.

Подобная конструкция используется в кватернионы.

Сложные корни единства

Три третьих корня из 1

Комплексное число ш такой, что ш^п = 1 для положительного целого числа п является пй корень единства. Геометрически пкорни из единицы лежат на единичной окружности комплексной плоскости в вершинах правильного п-угольник с одной вершиной на вещественном числе 1.

Если ш^п = 1 но ш^k ≠ 1 для всех натуральных чисел k такой, что 0 < k < п, тогда ш называется примитивный пй корень единства. Отрицательная единица -1 - единственный примитивный квадратный корень из единицы. В мнимая единица я является одним из двух примитивных корней 4-й степени единицы; другой -я.

Число е^2πi/п примитивный п-й корень из единства с наименьшим положительным аргумент. (Иногда его называют главный пй корень единства, хотя эта терминология не является универсальной и ее не следует путать с основная стоимость из ^п√1, что равно 1.^[25][26][27])

Другой пкорни из единства даются

${ displaystyle left (e ^ {{ frac {2} {n}} pi i} right) ^ {k} = e ^ {{ frac {2} {n}} pi ik}}$

для 2 ≤ k ≤ п.

Корни произвольных комплексных чисел

Хотя существует бесконечно много возможных значений для общего комплексного логарифма, существует только конечное количество значений для степени ш^q в важном частном случае, когда q = 1/п и п положительное целое число. Эти пкорни из ш; они являются решениями уравнения z^п = ш. Как и в случае с действительными корнями, второй корень также называется квадратным корнем, а третий корень также называется кубическим корнем.

В математике принято определять ш^1/п как основная стоимость корня, который обычно является пкорень th, аргумент которого имеет наименьший абсолютная величина. Когда ш положительное действительное число, это согласуется с обычным соглашением об определении ш^1/п как уникальный позитивный реальный пй корень. С другой стороны, когда ш отрицательное действительное число, и п нечетное целое число, единственное действительное пй корень не один из двух пкорни th, аргумент которых имеет наименьшее абсолютное значение. В этом случае значение ш^1/п может зависеть от контекста, и может потребоваться некоторая осторожность, чтобы избежать ошибок.

Набор пкорни th комплексного числа ш получается путем умножения главного значения ш^1/п каждым из пкорни единства. Например, корень четвертой степени из 16 равен 2, −2, 2.я, и −2я, потому что главное значение корня четвертой степени из 16 равно 2, а корни четвертой степени из единицы равны 1, −1, я, и -я.

Вычислительный комплекс мощности

Часто проще вычислить сложные степени, записав число, которое нужно возвести в степень в полярная форма. Каждое комплексное число z можно записать в полярной форме

${ Displaystyle г = ре ^ {я тета} = е ^ { ln (г) + я тета},}$

где р неотрицательное действительное число и θ это (настоящий) аргумент из z. Полярная форма имеет простую геометрическую интерпретацию: если комплексное число ты + iv считается представлением точки (ты, v) в комплексная плоскость с помощью Декартовы координаты, тогда (р, θ) это та же точка в полярные координаты. Это, р это "радиус" р² = ты² + v² и θ это "угол" θ = atan2 (v, ты). Полярный угол θ неоднозначно, так как любое целое кратное 2π может быть добавлено к θ без изменения местоположения точки. Каждый выбор θ дает в общем другое возможное значение мощности. А срезанная ветка можно использовать для выбора определенного значения. Главное значение (наиболее распространенный срез ветки) соответствует θ выбранный в интервале (−π, π]. Для комплексных чисел с положительной действительной частью и нулевой мнимой частью использование главного значения дает тот же результат, что и использование соответствующего действительного числа.

Чтобы вычислить комплексную мощность ш^z, записывать ш в полярной форме:

${ displaystyle w = re ^ {я theta}.}$

потом

${ Displaystyle журнал (ш) = пер (г) + я тета,}$

и поэтому

${ displaystyle w ^ {z} = e ^ {z log (w)} = e ^ {z ( ln (r) + i theta)}.}$

Если z разлагается как c + ди, то формула для ш^z можно записать более явно как

${ Displaystyle (г ^ {с} е ^ {- д тета}) е ^ {я (д ln (г) + с тета)} = (г ^ {с} е ^ {- д тета} ) { big [} cos { big (} d ln (r) + c theta { big)} + i sin { big (} d ln (r) + c theta { big )} { big]}.}$

Эта окончательная формула позволяет легко вычислить комплексные степени из разложения основания в полярную форму и показателя степени в декартову форму. Здесь он показан как в полярной форме, так и в декартовой форме (через тождество Эйлера).

В следующих примерах используется главное значение, обрезание ветви, которое вызывает θ быть в интервале (−π, π]. Вычислить я^я, записывать я в полярной и декартовой формах:

${ displaystyle { begin {align} i & = 1 cdot e ^ {{ frac {1} {2}} i pi}, i & = 0 + 1i. end {align}}}$

Тогда формула выше с р = 1, θ = π/2, c = 0, и d = 1, дает

${ displaystyle i ^ {i} = left (1 ^ {0} e ^ {- { frac {1} {2}} pi} right) e ^ {i left [1 cdot ln ( 1) +0 cdot { frac {1} {2}} pi right]} = e ^ {- { frac {1} {2}} pi} приблизительно 0,2079.}$

Аналогично, чтобы найти (−2)^{3 + 4я}, вычислим полярную форму −2:

${ Displaystyle -2 = 2e ^ {я pi}}$

и используйте приведенную выше формулу для вычисления

${ displaystyle (-2) ^ {3 + 4i} = (2 ^ {3} e ^ {- 4 pi}) e ^ {i [4 ln (2) +3 pi]} приблизительно (2,602 -1.006i) cdot 10 ^ {- 5}.}$

Величина комплексной мощности зависит от используемой ветви. Например, если полярная форма я = 1е^5πi/2 используется для вычисления я^я, мощность оказывается е^−5π/2; основная ценность я^я, вычисленное выше, равно е^{−π / 2}. Множество всех возможных значений для я^я дан кем-то^[28]

${ displaystyle { begin {align} i & = 1 cdot e ^ {{ frac {1} {2}} i pi + i2 pi k} mid k in mathbb {Z}, i ^ {i} & = e ^ {i left ({ frac {1} {2}} i pi + i2 pi k right)} & = e ^ {- left ({ frac { 1} {2}} pi +2 pi k right)}. End {align}}}$

Таким образом, существует бесконечное множество значений, которые являются возможными кандидатами на значение я^я, по одному на каждое целое число k. Все они имеют нулевую мнимую часть, поэтому можно сказать я^я имеет бесконечное количество допустимых реальных значений.

Несостоятельность тождеств силы и логарифма

Некоторые тождества для степеней и логарифмов для положительных действительных чисел не работают для комплексных чисел, независимо от того, как определены сложные степени и комплексные логарифмы как однозначные функции. Например:

Обобщения

Моноиды

Возведение в степень с целыми показателями может быть определено в любом мультипликативном моноид.^[30] Моноид - это алгебраическая структура состоящий из набора Икс вместе с правилом композиции ("умножения"), удовлетворяющим ассоциативный закон и мультипликативная идентичность, обозначаемый 1. Возведение в степень индуктивно определяется как

• ${ displaystyle x ^ {0} = 1}$ для всех ${ displaystyle x in X}$,
• ${ Displaystyle х ^ {п + 1} = х ^ {п} х}$ для всех ${ displaystyle x in X}$ и неотрицательные целые числа п,
• Если п отрицательное целое число, тогда ${ Displaystyle х ^ {п}}$ только определено^[31] если ${ displaystyle x}$ имеет обратный Икс.

Моноиды включают в себя множество структур, важных для математики, в том числе группы и кольца (при умножении), с более конкретными примерами последнего матричные кольца и поля.

Матрицы и линейные операторы

Если А квадратная матрица, то произведение А с собой п раз называется матричная мощность. Также ${ displaystyle A ^ {0}}$ определяется как единичная матрица,^[32] и если А обратима, то ${ displaystyle A ^ {- n} = left (A ^ {- 1} right) ^ {n}}$.

Матричные полномочия часто появляются в контексте дискретные динамические системы, где матрица А выражает переход от вектора состояния Икс какой-то системы в следующее состояние Топор системы.^[33] Это стандартная интерпретация Цепь Маркова, Например. потом ${ displaystyle A ^ {2} x}$ состояние системы после двух временных шагов и т. д .: ${ Displaystyle А ^ {п} х}$ состояние системы после п временные шаги. Матричная мощность ${ Displaystyle А ^ {п}}$ матрица перехода между текущим и текущим состояниями п шаги в будущее. Таким образом, вычисление степеней матрицы эквивалентно решению эволюции динамической системы. Во многих случаях мощности матриц целесообразно вычислить, используя собственные значения и собственные векторы.

Помимо матриц, более общие линейные операторы также может быть возведен в степень. Примером может служить производная оператор исчисления, ${ displaystyle d / dx}$, который является линейным оператором, действующим на функции ${ displaystyle f (x)}$ дать новую функцию ${ Displaystyle (д / дх) е (х) = е '(х)}$. В п-ой степени оператора дифференцирования является п-я производная:

${ displaystyle left ({ frac {d} {dx}} right) ^ {n} f (x) = { frac {d ^ {n}} {dx ^ {n}}} f (x) = f ^ {(n)} (x).}$

Эти примеры предназначены для дискретных показателей линейных операторов, но во многих случаях также желательно определять степени таких операторов с непрерывными показателями. Это отправная точка математической теории полугруппы.^[34] Подобно тому, как вычисление степеней матриц с дискретными показателями решает дискретные динамические системы, так же вычисление степеней матриц с непрерывными показателями решает системы с непрерывной динамикой. Примеры включают подходы к решению уравнение теплопроводности, Уравнение Шредингера, волновое уравнение, и другие уравнения в частных производных, включая временную эволюцию. Частный случай возведения в степень оператора производной нецелой степени называется дробная производная который вместе с дробный интеграл, является одной из основных операций дробное исчисление.

Конечные поля

А поле представляет собой алгебраическую структуру, в которой умножение, сложение, вычитание и деление четко определены и удовлетворяют своим знакомым свойствам. Например, действительные числа образуют поле, как и комплексные числа и рациональные числа. В отличие от этих знакомых примеров полей, которые все бесконечные множества, некоторые поля содержат только конечное число элементов. Самый простой пример - это поле с двумя элементами ${ Displaystyle F_ {2} = {0,1 }}$ с добавлением, определяемым ${ Displaystyle 0 + 1 = 1 + 0 = 1}$ и ${ displaystyle 0 + 0 = 1 + 1 = 0}$, и умножение ${ Displaystyle 0 CDOT 0 = 1 CDOT 0 = 0 CDOT 1 = 0}$ и ${ Displaystyle 1 cdot 1 = 1}$.

Возведение в степень в конечных полях имеет приложения в криптография с открытым ключом. Например, Обмен ключами Диффи-Хеллмана использует тот факт, что возведение в степень вычислительно недорого в конечных полях, тогда как дискретный логарифм (обратное возведение в степень) требует больших вычислительных ресурсов.

Любое конечное поле F обладает свойством уникальности простое число п такой, что ${ displaystyle px = 0}$ для всех Икс в F; это, Икс добавил к себе п раз равно нулю. Например, в ${ displaystyle F_ {2}}$, простое число п = 2 имеет это свойство. Это простое число называется характеристика поля. Предположим, что F поле характеристики п, и рассмотрим функцию ${ Displaystyle е (х) = х ^ {р}}$ что поднимает каждый элемент F к власти п. Это называется Автоморфизм Фробениуса из F. Это автоморфизм поля из-за Мечта первокурсника идентичность ${ displaystyle (x + y) ^ {p} = x ^ {p} + y ^ {p}}$. Автоморфизм Фробениуса важен в теория чисел потому что он генерирует Группа Галуа из F над своим простым подполем.

В абстрактной алгебре

Возведение в степень для целых показателей может быть определено для довольно общих структур в абстрактная алгебра.

Позволять Икс быть набор с властно-ассоциативный бинарная операция который записан мультипликативно. потом Икс^п определяется для любого элемента Икс из Икс и любые ненулевые натуральное число п как продукт п копии Икс, который рекурсивно определяется

${ displaystyle { begin {align} x ^ {1} & = x, x ^ {n} & = x ^ {n-1} x quad { text {for}} n> 1. end {выровнено}}}$

У одного есть следующие свойства

${ displaystyle { begin {align} (x ^ {i} x ^ {j}) x ^ {k} & = x ^ {i} (x ^ {j} x ^ {k}), && { текст {(ассоциативно-степенное свойство)}} x ^ {m + n} & = x ^ {m} x ^ {n}, (x ^ {m}) ^ {n} & = x ^ {mn }. end {выравнивается}}}$

Если операция имеет двусторонний элемент идентичности 1, то Икс⁰ определяется равным 1 для любого Икс:^{[нужна цитата ]}

${ displaystyle { begin {align} x1 & = 1x = x, && { text {(двусторонняя идентификация)}} x ^ {0} & = 1. end {align}}}$

Если операция также имеет двустороннюю обратное и ассоциативна, то магма это группа. Обратное Икс можно обозначить как Икс⁻¹ и следует всем обычным правилам для экспонентов:

${ displaystyle { begin {align} xx ^ {- 1} & = x ^ {- 1} x = 1, && { text {(двусторонний обратный)}} (xy) z & = x (yz ), && { text {(ассоциативный)}} x ^ {- n} & = (x ^ {- 1}) ^ {n}, x ^ {mn} & = x ^ {m} x ^ {- n}. end {выравнивается}}}$

Если операция умножения коммутативный (как, например, в абелевы группы ), то имеет место следующее:

${ displaystyle (xy) ^ {n} = x ^ {n} y ^ {n}.}$

Если бинарная операция написана аддитивно, как это часто бывает для абелевы группы, то «возведение в степень - это повторное умножение» можно интерпретировать как «умножение повторяется дополнение ". Таким образом, каждый из приведенных выше законов возведения в степень имеет аналог среди законов умножения.

Когда в наборе определены несколько ассоциативно-ассоциативных двоичных операций, любая из которых может быть повторена, обычно указывается, какая операция повторяется, помещая соответствующий символ в верхний индекс. Таким образом, Икс^∗п является Икс ∗ ... ∗ Икс, в то время как Икс^#п является Икс # ... # Икс, какими бы ни были операции ∗ и #.

Также используются надстрочные обозначения, особенно в теория групп, указывать спряжение. Это, г^час = час⁻¹gh, где г и час являются элементами некоторых группа. Хотя спряжение подчиняется некоторым из тех же законов, что и возведение в степень, оно ни в каком смысле не является примером повторного умножения. А подавлять является алгебраическая структура в котором эти законы сопряжения играют центральную роль.

По сетам

Если п натуральное число, и А - произвольное множество, то выражение А^п часто используется для обозначения набора упорядоченных п- пары элементов А. Это эквивалентно разрешению А^п обозначим множество функций из множества {0, 1, 2, ..., п − 1} к набору А; то ппара (а₀, а₁, а₂, ..., а_п−1) представляет функцию, которая отправляет я к а_я.

Для бесконечного количественное числительное κ и множество А, обозначение А^κ также используется для обозначения набора всех функций от набора размера κ до А. Это иногда пишут ^κА чтобы отличить его от кардинального возведения в степень, определенного ниже.

Эта обобщенная экспонента также может быть определена для операций над множествами или для множеств с дополнительными структура. Например, в линейная алгебра, имеет смысл проиндексировать прямые суммы из векторные пространства по произвольным индексным множествам. То есть мы можем говорить о

${ Displaystyle bigoplus _ {я in mathbb {N}} V_ {я},}$

где каждый V_я - векторное пространство.

Тогда если V_я = V для каждого я, полученная прямая сумма может быть записана в экспоненциальной записи как V^⊕N, или просто V^N при том понимании, что по умолчанию используется прямая сумма. Мы снова можем заменить набор N с количественным числом п получить V^п, хотя без выбора конкретного стандартного набора с мощностью п, это определяется только вплоть до изоморфизм. Принимая V быть поле р из действительные числа (рассматривается как векторное пространство над собой) и п быть некоторым натуральное число, мы получаем векторное пространство, которое чаще всего изучается в линейной алгебре, вещественное векторное пространство р^п.

Если основанием операции возведения в степень является набор, операция возведения в степень - это Декартово произведение если не указано иное. Поскольку несколько декартовых произведений производят п-кортеж, которая может быть представлена ​​функцией на множестве соответствующей мощности, S^N становится просто набором всех функции от N к S в таком случае:

${ Displaystyle S ^ {N} Equiv {е двоеточие N к S }.}$

Это согласуется с возведение в степень кардинальных чисел, в том смысле, что |S^N| = |S|^|N|, где |Икс| это мощность Икс. Когда "2" определяется как {0, 1}, у нас есть |2^Икс| = 2^|Икс|, где 2^Икс, обычно обозначаемый п(Икс), это набор мощности из Икс; каждый подмножество Y из Икс однозначно соответствует функции на Икс принимая значение 1 для Икс ∈ Y и 0 для Икс ∉ Y.

В теории категорий

В Декартова закрытая категория, то экспоненциальный Операция может использоваться для возведения произвольного объекта в степень другого объекта. Это обобщает Декартово произведение в категории наборов. Если 0 - это исходный объект в декартовой закрытой категории, то экспоненциальный объект 0⁰ изоморфен любому терминальному объекту 1.

Кардинальных и порядковых чисел

В теория множеств, есть экспоненциальные операции для кардинал и порядковые номера.

Если κ и λ кардинальные числа, выражение κ^λ представляет мощность набора функций из любого набора мощности λ к любому набору мощности κ.^[35] Если κ и λ конечны, то это согласуется с обычной арифметической экспоненциальной операцией. Например, набор из 3-х элементов из 2-элементного набора имеет мощность 8 = 2³. В кардинальной арифметике κ⁰ всегда 1 (даже если κ бесконечный кардинал или ноль).

Возведение в степень кардинальных чисел отличается от возведения в степень порядковых чисел, которое определяется предел процесс с участием трансфинитная индукция.

Повторное возведение в степень

Подобно тому, как возведение в степень натуральных чисел мотивируется повторным умножением, можно определить операцию, основанную на повторном возведении в степень; эту операцию иногда называют гипер-4 или тетрация. Повторение тетрации приводит к другой операции и т. Д., Концепция под названием гипероперация. Эта последовательность операций выражается Функция Аккермана и Обозначение Кнута со стрелкой вверх. Так же, как возведение в степень растет быстрее, чем умножение, которое растет быстрее, чем сложение, так и тетрация растет быстрее, чем возведение в степень. Оценивается на (3, 3), функции сложения, умножения, возведения в степень и тетрации дают 6, 9, 27 и 7625597484987 (= 3²⁷ = 3³³ = ³3) соответственно.

Пределы полномочий

Ноль в степени нуля дает ряд примеров пределов неопределенная форма 0⁰. Ограничения в этих примерах существуют, но имеют разные значения, показывая, что функция двух переменных Икс^у не имеет предела (0, 0). Можно подумать, в каких точках эта функция имеет предел.