Итерированная функция - Iterated function
В математика, повторяющаяся функция это функция Х → Х (то есть функция от некоторого набор Икс себе), который получается составление другая функция ж : Икс → Икс с собой определенное количество раз. Процесс многократного применения одной и той же функции называется итерация. В этом процессе, начиная с некоторого начального числа, результат применения данной функции снова вводится в функцию в качестве входных данных, и этот процесс повторяется.
Итерированные функции являются объектами изучения в Информатика, фракталы, динамические системы, математика и ренормгруппа физика.
Определение
Формальное определение повторяющейся функции на набор Икс следует.
Позволять Икс быть набором и ж: Икс → Икс быть функция.
Определение ж п как п-я итерация ж (обозначение введено Ганс Генрих Бюрманн[нужна цитата ][1][2] и Джон Фредерик Уильям Гершель[3][1][4][2]), куда п является неотрицательным целым числом:
и
куда я быИкс это функция идентичности на Икс и ж○грамм обозначает функциональная композиция. То есть,
- (ж○грамм)(Икс) = ж (грамм(Икс)),
всегда ассоциативный.
Поскольку обозначение ж п может относиться как к итерации (композиции) функции ж или же возведение в степень функции ж (последний обычно используется в тригонометрия ), некоторые математики[нужна цитата ] выбрать использовать ∘ для обозначения композиционного значения, написание ж∘п(Икс) для п-я итерация функции ж(Икс), как, например, ж∘3(Икс) смысл ж(ж(ж(Икс))). С той же целью ж[п](Икс) использовался Бенджамин Пирс[5][2] в то время как Альфред Прингсхайм и Жюль Мольк предложенный пж(Икс) вместо.[6][2][nb 1]
Абелево свойство и итерационные последовательности
В общем, для всех неотрицательных целых чисел выполняется следующее тождество м и п,
Это структурно идентично свойству возведение в степень который амап = ам + п, т.е. частный случай ж(Икс) = топор.
В общем случае для произвольных общих (отрицательных, нецелых и т. Д.) Показателей м и п, это соотношение называется функциональное уравнение переноса, ср. Уравнение Шредера и Уравнение Абеля. В логарифмическом масштабе это сводится к гнездовая собственность из Полиномы Чебышева, Тм(Тп(Икс)) = Тm n(Икс), поскольку Тп(Икс) = cos (п arccos (Икс)).
Соотношение (ж м)п(Икс) = (ж п)м(Икс) = ж мин(Икс) также имеет место, аналогично свойству возведения в степень, что (ам)п = (ап)м = амин.
Последовательность функций ж п называется Последовательность Пикара,[7][8] названный в честь Шарль Эмиль Пикар.
Для данного Икс в Икс, то последовательность ценностей жп(Икс) называется орбита из Икс.
Если ж п (Икс) = ж п+м (Икс) для некоторого целого числа м, орбита называется периодическая орбита. Наименьшее такое значение м для данного Икс называется период обращения. Смысл Икс сам называется периодическая точка. В обнаружение цикла проблема в информатике - это алгоритмический задача нахождения первой периодической точки на орбите и периода орбиты.
Фиксированные точки
Если ж(Икс) = Икс для некоторых Икс в Икс (то есть период орбиты Икс равно 1), то Икс называется фиксированная точка повторяющейся последовательности. Множество неподвижных точек часто обозначают как Исправить(ж ). Существует ряд теоремы о неподвижной точке которые гарантируют наличие фиксированных точек в различных ситуациях, в том числе Теорема Банаха о неподвижной точке и Теорема Брауэра о неподвижной точке.
Есть несколько методов для ускорение схождения последовательностей, произведенных итерация с фиксированной точкой.[9] Например, Метод Эйткена примененный к повторяющейся фиксированной точке известен как Метод Стеффенсена, и производит квадратичную сходимость.
Ограничивающее поведение
После итерации можно обнаружить, что есть наборы, которые сжимаются и сходятся к одной точке. В таком случае точка, к которой сходится, называется привлекательная фиксированная точка. И наоборот, повторение может привести к появлению точек, расходящихся от одной точки; это было бы в случае нестабильная фиксированная точка.[10] Когда точки орбиты сходятся к одному или нескольким пределам, набор очки накопления орбиты известен как установленный предел или ω-предельное множество.
Идеи притяжения и отталкивания обобщаются аналогично; можно разделить итерации на стабильные наборы и нестабильные множества, по поведению малых окрестности под итерацией. (Также см Бесконечные композиции аналитических функций.)
Возможны другие ограничения поведения; Например, блуждающие точки - это точки, которые удаляются и никогда не возвращаются даже близко к тому месту, откуда они начали.
Инвариантная мера
Если рассматривать эволюцию распределения плотности, а не динамику отдельных точек, то предельное поведение задается инвариантная мера. Его можно визуализировать как поведение облака точек или облака пыли при повторяющейся итерации. Инвариантная мера является собственным состоянием оператора Рюэля-Фробениуса-Перрона или оператор передачи, что соответствует собственному значению 1. Меньшие собственные значения соответствуют нестабильным, распадающимся состояниям.
В общем, поскольку повторная итерация соответствует сдвигу, передаточному оператору и сопряженному с ним оператору Оператор Купмана оба могут интерпретироваться как операторы сдвига действие на сдвинуть пространство. Теория подсдвиги конечного типа дает общее представление о многих повторяющихся функциях, особенно о тех, которые приводят к хаосу.
Дробные итерации и потоки, а также отрицательные итерации
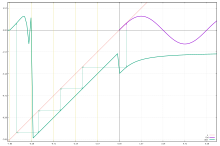
Понятие ж1/п следует использовать с осторожностью, когда уравнение граммп(Икс) = ж(Икс) имеет несколько решений, что обычно бывает, как в Уравнение Бэббиджа функциональных корней тождественной карты. Например, для п = 2 и ж(Икс) = 4Икс − 6, обе грамм(Икс) = 6 − 2Икс и грамм(Икс) = 2Икс − 2 решения; так что выражение ж ½(Икс) не обозначает уникальную функцию, так же как числа имеют несколько алгебраических корней. Проблема очень похожа на выражение "0/0 "в арифметике. Тривиальный корень ж всегда можно получить, если ж's область может быть достаточно расширена, ср. рисунок. Обычно выбираются корни, принадлежащие исследуемой орбите.
Можно определить дробную итерацию функции: например, половина повторения функции ж это функция грамм такой, что грамм(грамм(Икс)) = ж(Икс).[11] Эта функция грамм(Икс) может быть записано с использованием индексной записи как ж ½(Икс) . По аналогии, ж ⅓(Икс) функция, определенная таким образом, что ж⅓(ж⅓(ж⅓(Икс))) = ж(Икс), пока ж ⅔(Икс) можно определить как равный ж ⅓(ж ⅓(Икс))и т. д., все основано на упомянутом ранее принципе, что ж м○ж п = ж м + п. Эту идею можно обобщить так, чтобы количество итераций п становится непрерывный параметр, своего рода непрерывное «время» непрерывного орбита.[12][13]
В таких случаях систему называют поток. (см. раздел спаривание ниже.)
Отрицательные итерации соответствуют обратным функциям и их композициям. Например, ж −1(Икс) нормальная обратная ж, пока ж −2(Икс) является обратным, составленным с самим собой, т.е. ж −2(Икс) = ж −1(ж −1(Икс)). Дробно-отрицательные итерации определяются аналогично дробно-положительным; Например, ж −½(Икс) определяется так, что ж − ½(ж −½(Икс)) = ж −1(Икс), или, что то же самое, такое, что ж −½(ж ½(Икс)) = ж 0(Икс) = Икс.
Некоторые формулы для дробной итерации
Один из нескольких методов нахождения формулы ряда для дробной итерации с использованием фиксированной точки заключается в следующем.[14]
- Сначала определите фиксированную точку функции, такую что ж(а) = а .
- Определять ж п(а) = а для всех п принадлежащий к реалам. В некотором смысле это наиболее естественное дополнительное условие для дробных итераций.
- Расширять жп(Икс) вокруг фиксированной точки а как Серия Тейлор,
- Развернуть
- Заменить на ж k(а)= а, для любого k,
- Используйте геометрическая прогрессия чтобы упростить условия,
- Есть особый случай, когда ж '(а) = 1,
Это можно продолжать бесконечно, хотя и неэффективно, поскольку последние условия становятся все более сложными. Более систематическая процедура описана в следующем разделе, посвященном Спряжение.
Пример 1
Например, установка ж(Икс) = Сх + D дает фиксированную точку а = D/(1 − C), поэтому приведенная выше формула заканчивается просто
что тривиально проверить.
Пример 2
Найдите значение где это делается п раз (и, возможно, интерполированные значения, когда п не является целым числом). У нас есть ж(Икс) = √2Икс. Фиксированная точка а = ж(2) = 2.
Итак, установите Икс = 1 и ж п (1) расширенный вокруг значения фиксированной точки 2 представляет собой бесконечный ряд,
что, принимая только первые три члена, правильно до первого десятичного знака, когда п положительный - ср. Тетрация: ж п(1) = п√2. (Используя другую фиксированную точку а = ж(4) = 4 заставляет серию расходиться.)
За п = −1, ряд вычисляет обратную функцию 2+перИкс/пер. 2.
Пример 3
С функцией ж(Икс) = Иксб, развернитесь вокруг фиксированной точки 1, чтобы получить ряд
который представляет собой просто ряд Тейлора Икс(бп ) расширился около 1.
Спряжение
Если ж и грамм - две повторяющиеся функции, и существует гомеоморфизм час такой, что грамм = час−1 ○ ж ○ час, тогда ж и грамм как говорят топологически сопряженный.
Ясно, что топологическая сопряженность сохраняется при итерации, поскольку граммп = час−1 ○ ж п ○ час. Таким образом, если можно решить для одной системы повторяющихся функций, у него также есть решения для всех топологически сопряженных систем. Например, карта палатки топологически сопряжена логистическая карта. Как частный случай, принимая ж(Икс) = Икс + 1, есть итерация грамм(Икс) = час−1(час(Икс) + 1) в качестве
- граммп(Икс) = час−1(час(Икс) + п), для любой функции час.
Делаем замену Икс = час−1(у) = ϕ(у) дает
- грамм(ϕ(у)) = ϕ(у+1), форма, известная как Уравнение Абеля.
Даже в отсутствие строгого гомеоморфизма вблизи фиксированной точки, здесь принимаемой Икс = 0, ж(0) = 0, часто можно решить[15] Уравнение Шредера для функции, что делает ж(Икс) локально сопряжены с простым расширением, грамм(Икс) = ж '(0) Икс, то есть
- ж(Икс) = Ψ−1(ж '(0) Ψ (Икс)).
Таким образом, его итерационная орбита или поток при подходящих условиях (например, ж '(0) ≠ 1), составляет сопряжение орбиты монома,
- Ψ−1(ж '(0)п Ψ (Икс)),
куда п в этом выражении служит простой показатель степени: функциональная итерация сведена к умножению! Однако здесь показатель степени п больше не обязательно должно быть целым или положительным, и это непрерывное «время» эволюции для полной орбиты:[16] в моноид последовательности Пикара (ср. полугруппа преобразований ) обобщил до полной непрерывная группа.[17]

Этот метод (пертурбативное определение главного собственная функция Ψ, ср. Матрица Карлемана ) эквивалентен алгоритму из предыдущего раздела, хотя на практике более эффективен и систематичен.
Цепи Маркова
Если функция линейна и может быть описана стохастическая матрица, то есть матрица, сумма строк или столбцов которой равна единице, то итерированная система называется Цепь Маркова.
Примеры
Есть много хаотических карт. Хорошо известные повторяющиеся функции включают Набор Мандельброта и системы повторяющихся функций.
Эрнст Шредер,[19] в 1870 г. разработал частные случаи логистическая карта, например, хаотичный случай ж(Икс) = 4Икс(1 − Икс), так что Ψ (Икс) = arcsin2(√Икс), следовательно ж п(Икс) = грех2(2п arcsin (√Икс)).
Нехаотический случай, который Шредер также проиллюстрировал своим методом, ж(Икс) = 2Икс(1 − Икс), дал Ψ (Икс) = −1/2 ln (1-2Икс), и поэтому жп(Икс) = −1/2((1 − 2Икс)2п − 1).
Если ж это действие элемента группы на множестве, то итерированная функция соответствует свободная группа.
Большинство функций не имеют явного общего выражения в закрытой форме для п-я итерация. В таблице ниже перечислены некоторые[19] что делать. Обратите внимание, что все эти выражения действительны даже для нецелых и отрицательных п, а также неотрицательное целое число п.
| (смотрите примечание) | куда: |
| (смотрите примечание) | куда: |
| (рациональное разностное уравнение )[20] | куда: |
| (общий Уравнение Абеля ) | |
|
Примечание: эти два частных случая топор2 + bx + c являются единственными случаями, которые имеют решение в закрытой форме. Выбор б = 2 = –а и б = 4 = –асоответственно, еще больше сводит их к нехаотическим и хаотическим логистическим случаям, обсуждавшимся перед таблицей.
Некоторые из этих примеров связаны между собой простой связью. Еще несколько примеров, которые по существу представляют собой простые сопряжения примеров Шредера, можно найти в ссылке.[21]
Средства обучения
Итерированные функции можно изучать с помощью Дзета-функция Артина – Мазура и с операторы трансфера.
В информатике
В Информатика, повторяющиеся функции возникают как частный случай рекурсивные функции, которые, в свою очередь, закрепляют изучение таких широких тем, как лямбда-исчисление, или более узкие, такие как денотационная семантика компьютерных программ.
Определения в терминах повторяющихся функций
Два важных функционалы можно определить в терминах повторяющихся функций. Это суммирование:
и эквивалентный продукт:
Функциональная производная
В функциональная производная итерируемой функции задается рекурсивной формулой:
Уравнение переноса данных Ли
Итерированные функции возникают в последовательном расширении комбинированных функций, таких как грамм(ж(Икс)).
Учитывая скорость итераций, или же бета-функция (физика),
для пth итерация функции ж, у нас есть[22]
Например, для жесткой адвекции, если ж(Икс) = Икс + т, тогда v(Икс) = т. Как следствие, грамм(Икс + т) = ехр (т ∂/∂Икс) грамм(Икс), действие простой оператор смены.
И наоборот, можно указать ж(Икс) учитывая произвольный v(Икс)через общий Уравнение Абеля обсуждалось выше,
куда
Это очевидно, если отметить, что
Для индекса непрерывной итерации тто, теперь записанное как нижний индекс, это составляет знаменитую экспоненциальную реализацию Ли непрерывной группы:
Начальная скорость потока v достаточно для определения всего потока, учитывая эту экспоненциальную реализацию, которая автоматически дает общее решение функциональное уравнение переноса,[23]
Смотрите также
Примечания
- ^ Альфред Прингсхайм 'песок Жюль Мольк обозначение (1907 г.) пж(Икс) обозначать функциональные композиции не следует путать с Рудольф фон Биттер Рукер s (1982) обозначение пИкс, введенный Гансом Маурером (1901) и Рубен Луи Гудштейн (1947) для тетрация, или с Дэвид Паттерсон Эллерман s (1995) пИкс пре-верхний индекс для корни.
Рекомендации
- ^ а б Гершель, Джон Фредерик Уильям (1820). «Часть III. Раздел I. Примеры прямого метода различий». Сборник примеров приложений исчисления конечных разностей. Кембридж, Великобритания: Напечатано Дж. Смитом, продано J. Deighton & sons. С. 1–13 [5–6]. В архиве из оригинала 2020-08-04. Получено 2020-08-04. [1] (NB. Здесь Гершель ссылается на 1813 работа и упоминает Ганс Генрих Бюрманн более старая работа.)
- ^ а б c d Кахори, Флориан (1952) [март 1929]. «§472. Степень логарифма / §473. Итерированные логарифмы / §533. Обозначения Джона Гершеля для обратных функций / §535. Сохранение конкурирующих обозначений для обратных функций / §537. Полномочия тригонометрических функций». История математических обозначений. 2 (3-е исправленное издание номера 1929 г., 2-е изд.). Чикаго, США: Издательство open court. С. 108, 176–179, 336, 346. ISBN 978-1-60206-714-1. Получено 2016-01-18.
[…] §473. Итерированные логарифмы […] Здесь мы отмечаем символизм, используемый Pringsheim и Молк в их совместных Энциклопедия статья: "2бревноб а = журналб (бревноб а), …, k+1бревноб а = журналб (kбревноб а)."[а] […] §533. Джон Гершель обозначение обратных функций, грех−1 Икс, загар−1 Икси др., была опубликована им в Философские труды Лондона, за 1813 год. Он говорит (п. 10 ): "Это обозначение cos.−1 е не следует понимать как 1 / cos.е, но то, что обычно пишут так, arc (cos. =е). "Он признает, что некоторые авторы используют cos.м А для (cos.А)м, но он оправдывает свои собственные обозначения, указывая, что, поскольку d2 Икс, Δ3 Икс, Σ2 Икс иметь в виду дд Икс, ΔΔΔИкс, ΣΣИкс, мы должны написать грех.2 Икс за грех. грех.Икс, бревно.3 Икс для журнала. бревно. бревно.Икс. Как мы пишем d−п V = ∫п V, мы можем написать аналогично sin.−1 Икс= дуга (грех. =Икс), бревно.−1 Икс. = cИкс. Несколько лет спустя Гершель объяснил, что в 1813 году он использовал жп(Икс), ж−п(Икс), грех.−1 Икси т. д. ", как он тогда предполагал впервые. Работа немецкого аналитика, Бурманн, однако, в течение этих нескольких месяцев пришел к его знанию, в котором то же самое объясняется значительно раньше. Однако он [Бурманн], похоже, не заметил удобства применения этой идеи к обратным функциям tan−1и т. д., и при этом он, кажется, совсем не осведомлен об обратном исчислении функций, которое оно порождает ». Гершель добавляет:« Симметрия этой записи и, прежде всего, новые и наиболее обширные взгляды, которые она открывает на природу аналитических операций. похоже, санкционирует его всеобщее принятие ".[b] […] §535. Сохранение конкурирующих обозначений для обратной функции.- […] Использование обозначений Гершеля претерпело небольшие изменения в Бенджамин Пирс книги, чтобы снять главное возражение против них; Пирс писал: «потому что[−1] Икс," "бревно[−1] Икс."[c] […] §537. Степени тригонометрических функций.- Для обозначения, скажем, квадрата греха использовались три основных обозначения.Икс, а именно (грехИкс)2грехИкс2грех2 Икс. В настоящее время преобладающее обозначение - грех.2 Икс, хотя вероятность того, что первое будет неправильно истолковано, будет меньше всего. В случае греха2 Икс напрашиваются две интерпретации; во-первых, грехИкс · ГрехИкс; второй,[d] грех (грехИкс). Поскольку функции последнего типа обычно не проявляются, опасность неправильной интерпретации намного меньше, чем в случае журнала2 Икс, где журналИкс · бревноИкс и журнал (журналИкс) часто встречаются в анализе. […] Обозначение грехап Икс для (грехаИкс)п широко использовался и в настоящее время является преобладающим. […]
(xviii + 367 + 1 страница, включая 1 страницу дополнений) (NB. ISBN и ссылка для перепечатки 2-го издания компанией Cosimo, Inc., Нью-Йорк, США, 2013 г.) - ^ Гершель, Джон Фредерик Уильям (1813) [1812-11-12]. «Об одном замечательном применении теоремы Котеса». Философские труды Лондонского королевского общества. Лондон: Лондонское королевское общество, напечатано W. Bulmer and Co., Кливленд-Роу, Сент-Джеймс, продано G. and W. Nicol, Pall-Mall. 103 (Часть 1): 8–26 [10]. Дои:10.1098 / рстл.1813.0005. JSTOR 107384. S2CID 118124706.
- ^ Пеано, Джузеппе (1903). Formulaire mathématique (На французском). IV. п. 229.
- ^ Пирс, Бенджамин (1852). Кривые, функции и силы. я (новое изд.). Бостон, США. п. 203.
- ^ Pringsheim, Альфред; Молк, Жюль (1907). Энциклопедия чистых математических наук и прикладных наук (На французском). я. п. 195. Часть I.
- ^ Кучма, Марек (1968). Функциональные уравнения с одной переменной. Monografie Matematyczne. Варшава: PWN - Польское научное издательство.
- ^ Кучма М., Хочевски Б. и Гер Р. (1990). Итерационные функциональные уравнения. Издательство Кембриджского университета. ISBN 0-521-35561-3.
- ^ Карлесон, Л .; Гамелин, Т. Д. У. (1993). Сложная динамика. Universitext: трактаты по математике. Springer-Verlag. ISBN 0-387-97942-5.
- ^ Истратеску, Василе (1981). Теория неподвижной точки, введение, Д. Рейдел, Голландия. ISBN 90-277-1224-7.
- ^ «Нахождение такого f, что f (f (x)) = g (x) для данного g». MathOverflow.
- ^ Aldrovandi, R .; Фрейтас, Л. П. (1998). «Непрерывная итерация динамических карт». J. Math. Phys. 39 (10): 5324. arXiv:физика / 9712026. Bibcode:1998JMP .... 39.5324A. Дои:10.1063/1.532574. HDL:11449/65519. S2CID 119675869.
- ^ Берколайко, Г .; Рабинович, С .; Хавлин, С. (1998). "Анализ карлемановского представления аналитических рекурсий". J. Math. Анальный. Приложение. 224: 81–90. Дои:10.1006 / jmaa.1998.5986.
- ^ "Tetration.org".
- ^ Кимура, Тосихуса (1971). «Об итерации аналитических функций», Funkcialaj Ekvacioj 14, 197-238.
- ^ Кертрайт, Т.; Захос, К.К. (2009). «Профили эволюции и функциональные уравнения». Журнал физики А. 42 (48): 485208. arXiv:0909.2424. Bibcode:2009JPhA ... 42V5208C. Дои:10.1088/1751-8113/42/48/485208. S2CID 115173476.
- ^ Для явного примера, пример 2 выше составляет просто ж п(Икс) = Ψ−1((ln 2)п Ψ (Икс)), за любой n, не обязательно целое число, где Ψ - решение соответствующего Уравнение Шредера, Ψ (√2Икс) = ln 2 Ψ (Икс). Это решение также является бесконечным м предел (ж м(Икс) - 2) / (ln 2)м.
- ^ Кертрайт, Т. Поверхности эволюции и функциональные методы Шредера.
- ^ а б Шредер, Эрнст (1870). "Ueber iterirte Functionen". Математика. Анна. 3 (2): 296–322. Дои:10.1007 / BF01443992. S2CID 116998358.
- ^ Брэнд, Луи, «Последовательность, определяемая уравнением разности», Американский математический ежемесячный журнал 62, Сентябрь 1955 г., стр. 489–492. онлайн
- ^ Кацура, С .; Фукуда, В. (1985). «Точно решаемые модели, демонстрирующие хаотическое поведение». Physica A: Статистическая механика и ее приложения. 130 (3): 597. Bibcode:1985PhyA..130..597K. Дои:10.1016/0378-4371(85)90048-2.
- ^ Berkson, E .; Порта, Х. (1978). «Полугруппы аналитических функций и операторы композиции». Мичиганский математический журнал. 25: 101–115. Дои:10.1307 / mmj / 1029002009. Curtright, T. L .; Захос, К. К. (2010). «Хаотические отображения, гамильтоновы потоки и голографические методы». Журнал физики A: математический и теоретический. 43 (44): 445101. arXiv:1002.0104. Bibcode:2010JPhA ... 43R5101C. Дои:10.1088/1751-8113/43/44/445101. S2CID 115176169.
- ^ Aczel, J. (2006), Лекции по функциональному Уравнения и их приложения (Dover Книги по математике, 2006 г.), гл. 6, ISBN 978-0486445236.




























![{ frac {a} {c}} + { frac {bc-ad} {c}} left [{ frac {(cx-a + alpha) alpha ^ {n-1} - (cx-a + beta) beta ^ {n-1}} {(cx-a + alpha) alpha ^ {n} - (cx-a + beta) beta ^ {n}}} right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/80f439f7ab492078f725ac4f6c3b237ea4eb035a)


















![{ displaystyle g (f (x)) = exp left [v (x) { frac { partial} { partial x}} right] g (x).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/44cc4696d80602916c4349d9fa5247f3d9bd7ec4)




