Триаконтагон - Triacontagon

Обычный триаконтагон
Обычный триаконтагон
Тип	Правильный многоугольник
Края и вершины	30
Символ Шлефли	{30}, т {15}
Диаграмма Кокстера
Группа симметрии	Двугранный (D30), заказ 2 × 30
Внутренний угол (градусы )	168°
Двойной многоугольник	Себя
Характеристики	Выпуклый, циклический, равносторонний, изогональный, изотоксальный

В геометрия, а триаконтагон или 30-угольник - это тридцатигранный многоугольник. Сумма внутренних углов любого триаконтагона равна 5040 градусов.

Обычный триаконтагон

В обычный триаконтагон это конструктивный многоугольник, краем-деление пополам регулярного пятиугольник, а также может быть построен как усеченный пятиугольник, т {15}. Усеченный триаконтагон, t {30}, является шестиугольник, {60}.

Один внутренний угол в обычный триаконтагон равен 168 °, что означает, что один внешний угол будет 12 °. Триаконтагон - это самый большой правильный многоугольник, внутренний угол которого является суммой внутренних углов меньших многоугольников: 168 ° - это сумма внутренних углов равносторонний треугольник (60 °) и правильный пятиугольник (108°).

В площадь обычного триаконтагона (с т = длина кромки)

${ displaystyle A = { frac {15} {2}} t ^ {2} cot { frac { pi} {30}} = { frac {15} {2}} t ^ {2} left ({ sqrt {23 + 10 { sqrt {5}} + 2 { sqrt {3 (85 + 38 { sqrt {5}})}}}} right) = { frac {15} { 4}} t ^ {2} left ({ sqrt {15}} + 3 { sqrt {3}} + { sqrt {2}} { sqrt {25 + 11 { sqrt {5}}} }верно)}$

В inradius обычного триаконтагона

${ displaystyle r = { frac {1} {2}} t cot { frac { pi} {30}} = { frac {1} {4}} t left ({ sqrt {15} } +3 { sqrt {3}} + { sqrt {2}} { sqrt {25 + 11 { sqrt {5}}}} right)}$

В по окружности обычного триаконтагона

${ displaystyle R = { frac {1} {2}} t csc { frac { pi} {30}} = { frac {1} {2}} t left (2 + { sqrt { 5}} + { sqrt {15 + 6 { sqrt {5}}}} right)}$

Строительство

Обычный триаконтагон с данной описанной окружностью

Поскольку 30 = 2 × 3 × 5, правильный триаконтагон равен конструктивный используя компас и линейка.^[1]

Симметрия

Симметрии правильного треугольника, показанные с помощью цветов на ребрах и вершинах. Линии отражений синие по вершинам и пурпурные по краям. Гирации указаны цифрами в центре. Вершины окрашены в соответствии с их положением симметрии. Симметрии подгрупп соединены цветными линиями, индексами 2, 3 и 5.

В обычный триаконтагон есть Dih₃₀ двугранная симметрия, порядок 60, представленный 30 линиями отражения. Dih₃₀ имеет 7 диэдральных подгрупп: Dih₁₅, (Dih₁₀, Ди₅), (Dih₆, Ди₃) и (Dih₂, Ди₁). Также есть еще восемь циклический симметрии как подгруппы: (Z₃₀, Z₁₅), (Z₁₀, Z₅), (Z₆, Z₃) и (Z₂, Z₁), причем Z_п представляющий π /п радианная вращательная симметрия.

Джон Конвей обозначает эти более низкие симметрии буквой, а порядок симметрии следует за буквой.^[2] Он дает d (диагональ) с зеркальными линиями через вершины, п с зеркальными линиями по краям (перпендикулярно), я с зеркальными линиями через вершины и края, и грамм для вращательной симметрии. а1 этикетки не симметричны.

Эти более низкие симметрии позволяют степеням свободы определять нерегулярные триаконцентры. Только g30 подгруппа не имеет степеней свободы, но может рассматриваться как направленные края.

Рассечение

30-угольник с 420 ромбами

Coxeter заявляет, что каждый зоногон (а 2м-угольник, противоположные стороны которого параллельны и равной длины) можно разрезать на м(м-1) / 2 параллелограмма.^[3]В частности, это верно для правильных многоугольников с равным числом сторон, и в этом случае все параллелограммы являются ромбическими. Для обычный триаконтагон, м= 15, его можно разделить на 105: 7 наборов по 15 ромбов. Это разложение основано на Многоугольник Петри проекция 15-куб.

Примеры

Триаконтаграмма

Триаконтаграмма - это 30-гранная звездный многоугольник. Есть 3 обычные формы, которые дает Символы Шлефли {30/7}, {30/11} и {30/13}, а также 11 составных звездных фигур с одинаковыми конфигурация вершины.

Соединения и звезды
Форма	Соединения					Звездный многоугольник	Сложный
Рисунок	{30/2}=2{15}	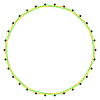{30/3}=3{10}	{30/4}=2{15/2}	{30/5}=5{6}	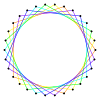{30/6}=6{5}	{30/7}	{30/8}=2{15/4}
Внутренний угол	156°	144°	132°	120°	108°	96°	84°
Форма	Соединения		Звездный многоугольник	Сложный	Звездный многоугольник	Соединения
Рисунок	{30/9}=3{10/3}	{30/10}=10{3}	{30/11}	{30/12}=6{5/2}	{30/13}	{30/14}=2{15/7}	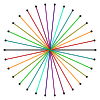{30/15}=15{2}
Внутренний угол	72°	60°	48°	36°	24°	12°	0°

Это также изогональный триаконтаграммы, построенные как более глубокие усечения регулярных пятиугольник {15} и пентадекаграммы {15/7}, и перевернутые пентадекаграммы {15/11} и {15/13}. Другие усечения образуют двойные покрытия: t {15/14} = {30/14} = 2 {15/7}, t {15/8} = {30/8} = 2 {15/4}, t {15 / 4} = {30/4} = 2 {15/4} и t {15/2} = {30/2} = 2 {15}.^[4]

Соединения и звезды
Квазирегулярный	Изогональный							Квазирегулярный Двойные покрытия
t {15} = {30}								т {15/14} = 2 {15/7}
т {15/7} = {30/7}								т {15/8} = 2 {15/4}
т {15/11} = {30/11}		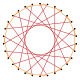						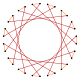т {15/4} = 2 {15/2}
т {15/13} = {30/13}								t {15/2} = 2 {15}

Полигоны Петри

Обычный триаконтагон - это Многоугольник Петри для трех 8-мерных многогранников с E₈ симметрия, показанная на ортогональные проекции в E₈ Самолет Кокстера. Это также многоугольник Петри для двух 4-мерных многогранников, показанных на H₄ Самолет Кокстера.

E8			ЧАС4
421	241	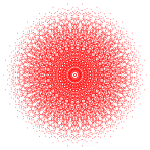142	120 ячеек	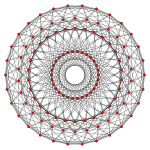600 ячеек

Регулярная триаконтаграмма {30/7} также является многоугольником Петри для большой звездчатый 120-элементный и большой 600-элементный.

Рекомендации

• Вайсштейн, Эрик В. «Триаконтагон». MathWorld.
• Именование многоугольников и многогранников
• триаконтагон